Приложенной к вращающемуся телу

Представим себе диск, вращающийся вокруг неподвижной оси под действием постоянной силы F (рис. 15.7), точка приложения которой пере­мещается вместе с диском. Разложим силу F на три взаимно перпендику­лярные составляющие: F₁ — окружная си­ла, F₂ — осевая сила, F₃ — радиальная си­ла. При повороте диска на бесконечно ма­лый угол d сила F совершит элементар­ную работу, которая на основании теоремы о работе равнодействующей будет равна сумме работ составляющих. Работа состав­ляющих F₂ и F₃ равна нулю, так как векто­ры этих сил перпендикулярны бесконечно малому перемещению ds точки приложе­ния М, поэтому элементарная работа силы F равна работе составляющей F₁:

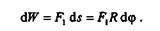
При повороте диска на конечный угол ср работа силы F равна

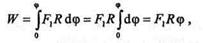
где угол выражается в радианах.

Так как моменты составляющих F₂ и F₃ относительно оси z равны нулю, то на основании теоремы Вариньона момент силы F относительно оси z равен

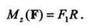
Момент силы, приложенной к диску, относительно оси вращения на­зывается вращающим моментом и, согласно стандарту ИСО, обозначается Т:

следовательно,

Работа постоянной силы, приложенной к вращающемуся телу, рав­на произведению вращающего момента на угловое перемещение.

Пример 15.3. Рабочий вращает рукоятку лебедки силой F = 200 Н, перпен­дикулярной радиусу вращения. Найти работу, затраченную в течение 25 с, если длина рукоятки r= 0,4 м, а угловая скорость ее 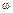= 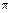/3 рад/с.

Решение. Прежде всего определим угловое перемещение 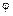рукоятки лебедки за 25 с:

Далее воспользуемся формулой для определения работы силы при враща­тельном движении:

Мощность

Работа, совершаемая какой-то силой, может быть осуществлена за различные промежутки времени. Чтобы охарактеризовать, насколько бы­стро совершается работа, в механике существует понятие мощности, обозначаемой Р.

Мощностью силы называется работа, совершаемая в единицу времени.

Если работа совершается равномерно, то мощность вычисляют по формуле

Если направление силы и направление перемещения совпадают, то эту формулу можно переписать в иной форме:

Мощность силы равна произведению модуля силы на скорость точ­ки ее приложения.

Единица мощности:

Если работа совершается силой, приложенной к вращающемуся телу, и притом равномерно, то мощность в этом случае вычисляют по формуле

Мощность силы, приложенной к вращающемуся телу, равна произ­ведению вращающего момента на угловую скорость.

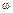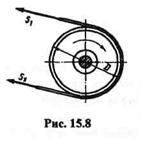
Пример 15.4. Посредством ремня передается мощность Р = 14,72 кВт. Диа­метр ременного шкива D = 1000 мм, угловая скорость = 5 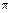рад/с. Предполагая натяжение S₁ ведущей ветви ремня вдвое большим натяжения S₂ ведомой ветви, определить S₁ и S₂ (рис. 15.8).

Решение. Разность натяжения ветвей равна силе трения, действующей меж­ду ремнем и шкивом, и в данном случае является окружной силой. Вращающий момент, действующий на шкив, равен

С другой стороны, вращающий момент можно вычислить, зная передавае­мую мощность и угловую скорость

Теперь можно определить натяжение S₂ ведомой ветви ремня:

По условию натяжение ведущей ветви в 2 раза больше натяжения ведомой, следовательно,