Теорема о работе силы тяжести
Теорема. Работа силы тяжести не зависит от вида траектории и равна произведению модуля силы на вертикальное перемещение точки ее приложения.
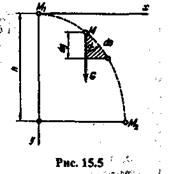
Пусть материальная точка М движется под действием одной лишь силы тяжести G и за какой-то промежуток времени перемещается из положения М1в положение М2, пройдя путь s (рис. 15.5).
|
На траектории точки М выделим бесконечно малый участок ds, который можно считать прямолинейным, и из его концов проведем прямые, параллельные осям координат, одна из которых вертикальна, а другая горизонтальна. Из заштрихованного треугольника получим, что
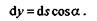
Элементарная работа силы G на пути ds
равна
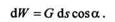
Полная работа на пути s равна
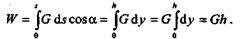
Итак,
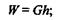
теорема доказана.
|
Силы, работа которых не зависит от вида траектории, называются потенциальными. К числу таких сил относятся, например, силы тяжести, силы всемирного тяготения, натяжение пружины.
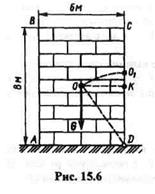
Пример 15.2. Однородный массив ABCD массой т = 4080 кг имеет размеры, указанные на рис 15.6. Определить работу, которую необходимо затратить на опрокидывание массива вокруг ребра D.
Решение. Определим силу тяжести G массива:
G = mg = 4080  9,81 = 40
9,81 = 40  103 Н = 40 кН.
103 Н = 40 кН.
Работа, которую необходимо затратить на опрокидывание массива, равна работе силы сопротивления, т. е. силы тяжести. Для того чтобы опрокинуть массив, необходимо его центр тяжести О (находящийся в геометрическом центре, так как массив однородный) перевести в положение O1, после чего массив продолжит опрокидываться под действием силы тяжести, которая превратится из силы сопротивления в движущую силу.
Искомую работу определим, применив теорему о работе силы тяжести:
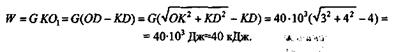
Дата добавления: 2021-09-07; просмотров: 586;











