Проекции силы на оси координат
В тех случаях, когда на тело действует более трех сил, а также когда неизвестны направления некоторых сил, удобнее при решении задач пользоваться не геометрическим, а аналитическим условием равновесия, которое основано на методике проекций.
Проекцией силы на ось называется отрезок оси, заключенный между двумя перпендикулярами, опущенными на ось из начала и конца вектора силы.
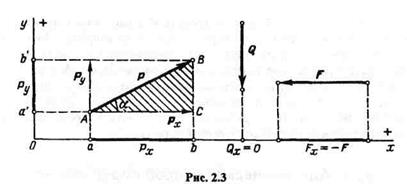
Пусть даны координатные оси х, у,сила Р, приложенная в точке А и расположенная в плоскости координатных осей (рис. 2.3).
Проекциями силы Р на оси будут отрезки аb и а'b'.Обозначим эти проекции соответственно Рх и Ру. Тогда

Проекция силы на ось есть величина алгебраическая, которая может быть положительной или отрицательной, что устанавливается по направлению проекции. За направление проекции примем направление от проекции начала к проекции конца вектора силы.
Установим следующее правило знаков:
если направление проекции силы на ось совпадает с положительным направлением оси, то эта проекция считается положительной, и наоборот.
Если вектор силы параллелен оси,то он проецируется на эту ось в натуральную величину (рис. 2.3, сила F).
Если вектор силы перпендикулярен оси, то его проекция на эту ось равна нулю (рис. 2.3, сила Q).
Зная две проекции Рх и Ру,из треугольника ABC определяем модуль и направление вектора силы Р по следующим формулам:
модуль силы
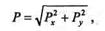
|
| направляющий тангенс угла между вектором силы Р и осью х |
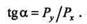
|
Отметим, что силу Р можно представить как равнодействующую двух составляющих сил Рх и Py,параллельных осям координат (рис. 2.3). Составляющие Рх и Py,и проекции Рх и Py,принципиально отличны друг от друга, так как составляющая есть величина векторная, а проекция — величина алгебраическая; но проекции силы на две взаимно перпендикулярные оси х и у и модули составляющих той же силы соответственно численно равны, когда сила раскладывается по двум взаимно перпендикулярным направлениям, параллельным осям х и у.
Дата добавления: 2021-09-07; просмотров: 641;











