Принцип освобождаемое
Связями называют ограничения, налагаемые на положения и скорости точек тела в пространстве. Сила, с которой тело действует на связь, называется силой давления; сила, с которой связь действует на тело, называется силой реакции или просто реакцией. Согласно аксиоме взаимодействия, эти силы по модулю равны и действуют по одной прямой в противоположные стороны. Силы реакций и дав-
лений приложены к различным телам и поэтому не представляют собой систему сил.
Силы, действующие на тело, делятся на активные и реактивные. Активные силы стремятся перемещать тело, к которому они приложены, а реактивные препятствуют этому перемещению. Принципиальное отличие активных сил от реактивных заключается в том, что значение реактивных сил, вообще говоря, зависит от значения активных сил, но не наоборот. Активные силы часто называют нагрузками.
При решении большинства задач статики несвободное тело условно изображают как свободное с помощью так называемого принципа осво-бождаемости, который формулируется так: всякое несвободное тело можно рассматривать как свободное, если отбросить связи, заменив их реакциями.
В результате применения этого принципа получаем тело, свободное от связей и находящееся под действием некоторой системы активных и реактивных сил.
Направление реакций определяется тем, в каком направлении данная связь препятствует перемещению тела. Правило для определения направления реакций можно сформулировать так: направление реакции связи противоположно направлению перемещения, не допускаемого данной связью.
Если связи считать идеально гладкими, то во многих случаях можно сразу указать направление их реакций. Рассмотрим направление реакций основных видов связей, встречающихся в различных конструкциях.
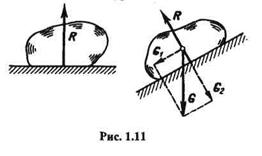
1. Идеально гладкая плоскость (рис. 1.11). В этом случае реакция R направлена перпендикулярно опорной плоскости в сторону тела, так как такая связь не дает телу перемещаться только в сторону опорной плоскости и перпендикулярно ей.
|
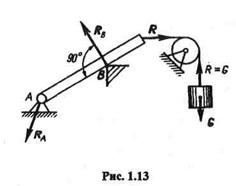
Если тело находится на наклонной плоскости, то, разложив силу тяжести Gна две составляющие G1 и G2, параллельную и перпендикулярную опорной плоскости, можно видеть, что составляющая G1 будет перемещать тело вдоль плоскости, а составляющая G2 будет прижимать тело к плоскости и уравновешиваться реакцией R.
|
|
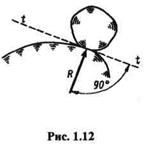
2. Идеально гладкая поверхность (рис. 1.12). В этом случае реакция R направлена перпендикулярно касательной плоскости t—t, т. е. по нормали к опорной поверхности в сторону тела, так как нормаль есть единственное направление перемещения тела, которое не допускает данная связь.
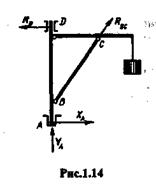
3. Закрепленная точка или ребро угла (рис. 1.13, ребро В).В этом случае реакция RB направлена по нормали к поверхности идеально гладкого тела в сторону тела, так как нормаль к поверхности тела есть единственное направление перемещения, которое не допускают эти связи.
4. Гибкая связь (рис. 1.13). Реакция R гибкой связи не дает телу лишь удаляться от точки подвеса и поэтому направлена вдоль связи от тела к точке подвеса. Из рис. 1.13 видно, что гибкая связь, перекинутая через блок, изменяет направление передаваемого усилия (натяжения нити).
В конструкциях широкое распространение имеют связи, которые называют шарнирами. Шарнир представляет собой подвижное соединение двух тел, допускающее только вращение вокруг общей оси (цилиндрический шарнир) или общей точки (шаровой шарнир).
5. Идеально гладкий цилиндрический шарнир
(рис. 1.13, шарнир А;рис. 1.14, подшипник D). В этом случае заранее из
вестно только, что реакция RA проходит через ось шарнира и перпенди
кулярна этой оси, так как шарнирное соединение допускает вращение
вокруг оси, но не допускает любое перемещение тела, перпендикулярное
этой оси.
6. Идеально гладкий шаровой шарнир. В этом случае
заранее известно только, что реакция проходит через центр шарнира, так
как тело, закрепленное в шаровом шарнире, может поворачиваться в любом направлении, но не может совершать никаких линейных перемеще
ний в пространстве.
7. Идеально гладкий подпятник (рис. 1.14, подпятник A). Подпятник можно рассматривать как сочетание цилиндрического шарнира и опорной плоскости. Поэтому будем считать реакцию подпятника состоящей из двух составляющих: ХA и YA.Полная реакция RА подпятника равна векторной сумме этих составляющих:
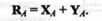
8. Стержень, закрепленный двумя концами в идеально гладких шарнирах и нагруженный только по концам (рис. 1.14, стержень ВС).В этом случае реакция стержня, согласно аксиоме III, может быть направлена только по линии ВС,т. е. по прямой, соединяющей оси шарниров.
В дальнейшем мы нередко будем встречаться с элементами различных конструкций, называемых брусьями. Брусом принято считать твердое тело, у которого длина значительно больше поперечных размеров; множество (геометрическое место) центров тяжести всех поперечных сечений называется осью бруса. Брус с прямолинейной осью, положенный на опоры и изгибаемый приложенными к нему нагрузками, называют балкой.
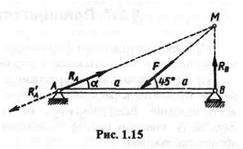
Пример 1.2. Определить направление реакций опор балки АВ,шарнирно закрепленной на неподвижной опоре А и опоре В,положенной на катки; указать направление силы давления балки на опору А (рис. 1.15). Силой тяжести балки пренебречь.
Решение. Применив принцип освобожцаемости, отбросим связи балки, т.е. опоры А и В, и заменим их реакциями RA и RB. Реакция RB подвижного шарнира перпендикулярна опорной плоскости, так как это единственное направление перемещения, не допускаемое данной связью. Реакция RA неподвижного шарнира проходит через ось, и согласно теореме о равновесии трех непараллельных сил, пиния действия этой реакции должна проходить через точку М.Реакция RA будет направлена по линии AM вправо и вверх, так как если опору А мысленно отбросить, то без реакции конец А балки будет под действием силы F перемещаться влево и вниз.
|
Согласно третьему закону Ньютона, сила давления R'A балки на опору также будет направлена по линии AM,но в противоположную сторону. Определим угол  :
:
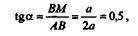
отсюда
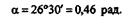
Дата добавления: 2021-09-07; просмотров: 779;











