Равнодействующей плоской системы сходящихся сил
Система сил, линии действия которых лежат в одной плоскости и все пересекаются в одной точке, называется плоской системой сходящихся сил.
Теорема.Плоская система сходящихся сил в общем случае эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих.
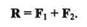
|
| Пользуясь той же аксиомой параллелограмма, сложим равнодействующую R с силой F3: |
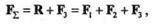
|
где F 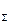 — равнодействующая данной системы трех сил. — равнодействующая данной системы трех сил.
|
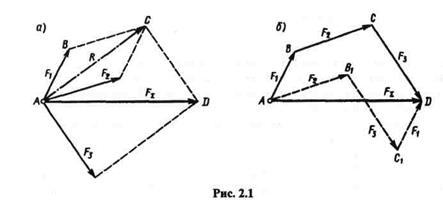
Пусть дана плоская система трех сил F1, F2 и F3, линии действия которых сходятся в точке А. На основании следствия из аксиом III и IV перенесем эти силы вдоль линий их действия в точку А.Сложив первые две силы F1 и F2 по правилу параллелограмма, получим их равнодействующую R (рис. 2.1, a):
|
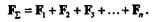
|
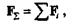
|
| Аналогичные рассуждения можно провести для любого количества сходящихся сил, в результате чего получим |
| Сокращенно это равенство запишем так: |
где i — все целые числа от 1 до n, а греческая заглавная буква 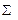 (сигма) означает сумму.
(сигма) означает сумму.
Очевидно, что построение, выполненное на рис. 2.1, а, можно заменить более простым (рис. 2.1, б). Многоугольник ABCD называется силовым многоугольником. Сторона AD,соединяющая начало первого с концом последнего вектора, называется замыкающей стороной.
Необходимо помнить, что стрелки векторов слагаемых сил образуют определенное направление обхода по контуру силового многоугольника, а замыкающая сторона, определяющая модуль и направление равнодействующей, имеет стрелку, направленную против обхода (рис. 2.1, б).
Если определить равнодействующую из силового многоугольника с помощью геометрии и тригонометрии, то такой способ будет называться геометрическим.
Если сделать чертеж силового многоугольника в определенном масштабе, то равнодействующая определится простым измерением замыкающей стороны с последующим умножением на масштаб. Такой способ нахождения равнодействующей называется графическим.
Порядок сложения векторов при построении силового многоугольника на величину равнодействующей не влияет, так как векторная сумма от перемены мест слагаемых не меняется (рис. 2.1, б,многоугольник AB1C1D).
Дата добавления: 2021-09-07; просмотров: 538;











