Плоской системы сходящихся сил
При построении силового многоугольника возможен случай, когда конец последнего вектора совпадает с началом первого. В этом случае замыкающей стороны не будет, и такой силовой многоугольник называется замкнутым.
Очевидно, что равнодействующая F 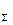 системы сходящихся сил,
системы сходящихся сил,
дающих замкнутый силовой многоугольник, равна нулю и, следовательно, эта система эквивалентна нулю, т. е. находится в равновесии. Отсюда вытекает условие, при котором плоская система сходящихся сил будет находиться в равновесии. Это условие выражается равенством
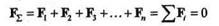
и формулируется так: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник был замкнут.
Условия равновесия, записанные в виде равенств, содержащих неизвестные величины,называются уравнениями равновесия.
Применяя геометрическое условие равновесия, удобно решать задачи, в которых на тело действуют три силы, так как в этом случае замкнутый силовой многоугольник представляет собой треугольник.
Решение большинства задач статики проводят в три этапа:
1) выбирают тело, равновесие которого будет рассматриваться;
2) отбрасывают связи, заменяя их реакциями, и устанавливают, какая система сил действует на тело;
3) пользуясь условиями равновесия, находят неизвестные величины.
При решении задач технической механики необходимо строго соблюдать правило: размерности и единицы величин всех слагаемых и обеих частей равенства должны быть одинаковыми.
Пользуясь этим правилом, целесообразно в сомнительных случаях проверять правильность хода решения задач, для чего следует поставить в слагаемые проверяемого равенства единицы всех входящих в него величин и, произведя возможные сокращения, сравнить полученные единицы правой и левой частей.
Проверим таким способом приведенную в § 1.6 формулу Q = ql:
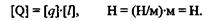
Единицы правой и левой частей равенства одинаковы, следовательно, формула по размерности верна.
Следует заметить, что такая проверка ничего не говорит о правильности нередко входящих в формулы числовых коэффициентов.
|
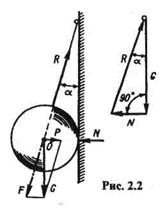
Пример 2.1. К вертикальной гладкой стене на веревке, составляющей со стеной угол а, подвешен однородный шар (рис. 2.2). Определить натяжение веревки F и силу давления шара Р на стену, если сила тяжести шара G.
Решение. Рассмотрим равновесие шара. Применив принцип освобождаемости, отбросим связи и заменим их реакциями. Реакция N гладкой стены перпендикулярна стене и проходит через центр шара. Так как шар однородный, то сила тяжести G приложена в его геометрическом центре. Реакция Rнаправлена вдоль веревки и, согласно теореме о равновесии трех непараллельных сил, ее линия действия также должна проходить через центр шара. Ксистеме трех сходящихся сил, приложенных к шару, применим геометрическое условие равновесия:
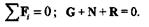
Строим замкнутый силовой многоугольник, начиная с изображения в произвольном масштабе вектора известной силы G.
Направление обхода треугольника (т. е. направление стрелок) определяется этой силой. Решая треугольник, получим
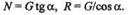
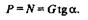
|
| Натяжение F веревки по модулю равно ее реакции R: |
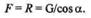
|
Искомая сила давления Р шара на стену, согласно аксиоме взаимодействия, по модулю равна реакции Nстены, но направлена в противоположную сторону:
Эту же задачу можно решить, разложив силу тяжести G по реальным направлениям (направлениям реакций) на составляющие Р (сила давления шара на стену) и F (натяжение веревки), причем, согласно аксиоме взаимодействия, F = R, Р = N.
Из построенного параллелограмма (рис. 2.2) легко определяем искомые величины. Такой метод решения задачи называют методом разложения.
Дата добавления: 2021-09-07; просмотров: 526;











