Описание движения жидкости и газа

В отличие от материальных точек, когда для описания их движения задавались координаты этих точек, а затем определялись их скорости и ускорения, для описания движения жидкости применяется несколько иной метод. Развитие этого метода связано с практическими успехами гидро- и аэродинамики. Аналитические формулы, описывающие движения тел в жидкости, очень громоздки, к тому же они содержат большое количество параметров. На практике более эффективным оказался метод моделирования, когда уменьшенные модели самолетов и судов в неподвижном состоянии помещались в аэродинамические трубы или испытательные бассейны. При этом измерялись скорости и ускорения потока жидкости или газа в различных точках испытываемой модели. При таком методе описания движения жидкости или газа измеряется не скорость (ускорение) различных частиц, а скорости и ускорения в некоторых фиксированных точках, через которые проходят отдельные частицы (или отдельные выделенные малые объемы). Если в любой такой выбранной точке значения скорости (или ускорения) не меняются с течением времени, то такое движение называется стационарным.

Обычно различают два типа движения жидкости: ламинарное и турбулентное. При ламинарном течении жидкость перемещается слоями, причем один слой скользит по другому, но слои не перемешиваются между собой, в турбулентном же движении наиболее характерным признаком является наличие вихрей.

Характер движения на первый взгляд зависит от величины скорости жидкости, но в действительности важную роль играют и другие факторы, в частности, вязкость или внутреннее трение. Это свойство органически присуще почти всем реальным жидкостям и является следствием взаимодействия молекул между собой. При ламинарном движении слои жидкости с трением скользят друг по другу. Чем сильнее силы сцепления между частицами жидкости, тем больше различие скоростей двух соседних слоев. Иначе говоря, степень быстроты изменения скорости слоев жидкости при перемещении перпендикулярно ее движению характеризует величину силы трения между слоями. Если же в жидкости движется твердое тело, то слой жидкости, непосредственно к нему прилегающий, движется с ним вместе, следующий слой скользит по первому слою с меньшей скоростью, следующий за вторым слой имеет еще меньшую скорость и т.д. Слой же, граничащий со стенками, ограничивающими поток жидкости, прилипает к стенкам так, что его скорость равна нулю. Величина силы трения при движении тела в жидкости установлена еще Ньютоном, который нашел ее аналитическое выражение:

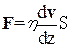, (9.1)

где первый сомножитель характеризует вязкость жидкости (коэффициент вязкости), второй отражает быстроту изменения скорости в направлении, перпендикулярным потоку (производная по направлению), и третий представляет площадь соприкосновения жидкости и тела, т.е. зависит от формы тела. Очевидно, что величина силы трения для каждого тела имеет свою определенную величину, но конкретный учет всех особенностей тела связан с серьезными математическими трудностями. Наиболее простой вид силы трения получается при движении шара:

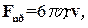(9.2)

где r - радиус шара, v - его скорость, h - коэффициент вязкости. Это выражение впервые получено Стоксом и известно как формула Стокса.

Степень влияния вязкости на характер движения жидкости можно оценить, если сравнить величину кинетической энергии движущегося тела с работой сил вязкого трения. Эта оценка производится весьма приближенно, c точностью до численных коэффициентов. Для обтекания вязкой жидкостью неподвижного шара величина кинетической энергии жидкости оценивается в предположении, что объем жидкости, где происходит возмущение потока, по своей величине примерно равен объему шара, так что величина кинетической энергии этого объема примерно равна:

Е_кин = 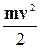~ r_жl³ υ², (9.3)

где l - линейные размеры шара. Для оценки величины работы силы вязкого трения предположим, что площадь поверхности шара S ~ l², и изменение скорости от значения υ до нуля также происходит на расстоянии l, т.е. Dυ ~ υ, Dz ~ l и

F_тр ~ h 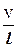l² ~ hυl , (9.4)

откуда следует, что работа силы трения А_тр равна:

А_тр ~ F_тр l ~ hυl ²_. (9.5)

Сравнивая (9.3 ) и (9.5), нетрудно получить:

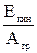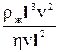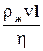~ ~ = Re. (9.6)

Подобные рассуждения можно провести для тела любой формы, поэтому безразмерная величина Re (9.6), получившая название числа Рейнольдса, позволяет оценить влияние вязкости жидкости на характер ее движения. Если число Рейнольдса велико, то трением в жидкости можно пренебречь и считать жидкость идеальной. Хотя введение числа Рейнольдса проведено в некотором приближении, тем не менее, по его величине можно судить не только о роли трения, но и о характере движения жидкости. Так, например, при Re ~ 1000 движение жидкости в трубах остается ламинарным, но при Re ~ 2200 оно становится турбулентным. При малых значениях чисел Рейнольдса роль вязкости жидкости достаточно велика и вихревого движения возникнуть не может.