Q – сила полезного сопротивления.
Силой полезного сопротивления называется сила, для преодоления которой предназначен механизм. Она приложена к ведомому звену со стороны внешних объектов. Природа этой силы может быть различной: сила резания, сила трения, сила упругости, сила гидравлического сопротивления и т.д. Работа силы полезного сопротивления всегда отрицательна. Сила полезного сопротивления тоже может являться функцией кинематических параметров.
F – сила вредного сопротивления.
Силами вредного сопротивления являются силы трения в кинематических парах, силы гидравлического и аэродинамического сопротивления. Работа этих сил отрицательна. При проектировании механизмов стремятся уменьшить эти силы, однако полностью избавиться от них невозможно.
G - сила тяжести.
Сила тяжести выражается через массу тела по формуле G = mg. Она приложена к телу в центре масс. Работа силы тяжести при опускании центра масс положительна, при поднимании - отрицательна. Работа силы тяжести за полный цикл движения механизма равна нулю.
R – сила реакции в кинематической паре.
Действие одного звена на другое проявляется в виде реакции. По своей природе реакция является силой упругости. Согласно 3-му закону Ньютона реакции двух взаимодействующих тел равны по величине и противоположны по направлению. Для механизма в целом работа сил реакции равна нулю.
U – сила инерции.
Объяснить сущность понятия «сила инерции» гораздо сложнее, чем всех остальных сил. В то же время это чрезвычайно важно для понимания динамических процессов. Поэтому рассмотрим эту силу более обстоятельно.
3.3. Сила инерции
Согласно 2-му закону Ньютона, ускорение, сообщаемое телу, пропорционально действующей силе, направлено по этой силе и обратно пропорционально массе тела:
a = F/m или F = ma . (3.1)
Этот закон справедлив только в инерциальных системах отсчета, т.е. в системах покоящихся или движущихся равномерно, прямолинейно относительно абсолютной мировой системы отсчета. В качестве таковой принимают систему с началом в центре Солнца и осями, направленными на три звезды. Земля с некоторым приближением также считается инерциальной системой. Иногда удобно изучать движение в неинерциальной системе отсчета, т.е. движущейся относительно Земли с ускорением. Для этого случая механика Ньютона, вообще говоря, непригодна. Однако оказалось возможным ее исправить, введя лишь некоторые поправки. Пусть на тело массой m, находящееся в сложном движении, действует сила F. В неподвижной (инерциальной) системе координат xy справедлив закон Ньютона:
F = ma, где a - ускорение в системе xy. С учетом кинематической теоремы Кориолисаможно записать:
F = m ( aE + aK + aR).
Перепишем полученное выражение следующим образом:
F - m( aE + aK) = m aR . (3.2)
Эта зависимость определяет закон движения в переносной неинерциальной системе ξη. Основываясь на аналогии с формулой (3.1), ее можно рассматривать как закон Ньютона для неинерциальной системы. Для этого следует рассматривать левую часть формулы (3.2) как силу. Выражение
U= - m ( aE + aK)
называют силой инерции. Если тело покоится в системе ξη, то
aK = aR = 0, тогда
F - maE = 0, F + U = 0.
Таким образом, мы приходим к принципу Даламбера: сумма активной силы F и силы инерции U, приложенных к телу, равна нулю. Принцип Даламбера позволяет динамическую задачу свести к задаче на равновесие сил, т.е. к задаче статики.
Более подробно о принципе Даламбера.
Механизм представляет собой систему связанных между собой материальных тел, обычно называемых звеньями. Движение каждого звена происходит под действием приложенных к нему активных сил и реакций связей со стороны соседних звеньев. Реакции связей есть силы более сложной структуры, чем активные силы. Если активные силы полностью определены внешними условиями и от движения звеньев не зависят, то реакции связей зависят как от внешних сил, так и от движения звеньев.
Для механизма на основе второго закона Ньютона можно составить столько дифференциальных уравнений, сколько подвижных звеньев у механизма. Задача получается очень сложной.
Полученная система уравнений в принципе может быть решена только в том случае, если известны зависимости реакций связей от координат точек системы (от конфигурации системы), т.е. упругость связей.
Обойти возникающее затруднение смог Даламбер, предложивший метод, носящий название «принцип Даламбера.» Если нельзя вычислить реакции связей, то их надо исключить, составив специальным образом уравнение движения.
В принципе Даламбера, прежде всего, вводится гипотеза об абсолютно жестких связях. В реальных механизмах эта гипотеза вполне оправдана, так как упругость связей, в связи с малой деформацией звеньев, практически не изменяет движение.
Следующим моментом в принципе Даламбера является сведение задачи о движении к задаче о равновесии . Это уже было рассмотрено выше. Таким образом имеем:
F -ma + R = 0.
Отсюда видно, что вектор (F-ma) уравновешивается силами, действующими со стороны связей. Поэтому к вектору (F-ma) можно применить принцип возможных перемещений, состоящий в том, что в случае равновесия системы сил, сумма работ всех сил, приложенных к телу на возможном перемещении, равна нулю. Это является третьим моментом в принципе Даламбера. Из получившихся уравнений реакции связей исключаются, так как при абсолютно жестких связях, перемещение в направлении сил, действующих со стороны связей, невозможно.
Принцип Даламбера не вводит никаких новых сил. До Даламбера представление об абсолютно жестких связях применялось редко. После Даламбера это представление стало широко использоваться, так как оно очень упрощало задачу и, вместе с тем, позволяло достаточно точно описать движение. В дальнейшем в формулировку принципа Даламбера стали вводить термин «силы инерции», называя этим словом вектор -ma.Однако для неподвижного наблюдателя никаких сил, кроме активной силы F и реакции R, нет, поэтому выражение -ma вообще не сила. Если бы –ma признать силой, то оказалось бы, что сумма всех сил равна нулю, но, несмотря на это, тело обладает ускорением, отличным от нуля, кроме того, неизвестно, откуда эта сила взялась, т.к. нет других тел, которые могли бы ее вызвать.
Однако приведенным разъяснением не исчерпываются все интерпретации принципа Даламбера, в связи с чем и возникают различные понимания авторами этого принципа и споры вокруг термина «силы инерции». Одна из точек зрения состоит в следующем. Поскольку тело М движется с ускорением a, то это означает, что оно находится под действием сил со стороны других тел, равнодействующая которых равна ma. Это означает, что, согласно третьему закону, ускоренное тело М действует на ускоряющее тело с силой –ma. Выражение –ma может быть названо силой инерции, и оно на самом деле является силой. Однако эта сила приложена к ускоряющим телам, а не к ускоряемому телу М. Поэтому принцип Даламбера можно интерпретировать и так: если к ускоряемому телу М приложить активную силу F, силу реакции R и силу инерции –ma, то они в сумме дают нуль, т.е. уравновешивают друг друга. Однако это равновесие является фиктивным, т.к. мы получаем нуль в результате сложения сил, действующих на разные тела. Поэтому часто в формулировку принципа Даламбера к термину «силы инерции» добавляют «фиктивные».
Резюмируя сказанное, сделаем вывод, что можно вкладывать различный смысл в понятие «силы инерции», однако в каждом случае следует пояснять ту точку зрения, с которой это понятие введено. В противном случае — неизбежна путаница.
При решении динамических задач возможны два подхода – с точки зрения наблюдателей, находящихся в инерциальной и неинерциальной системах. Первый наблюдатель для объяснения явления использует 2-ой закон Ньютона, второй наблюдатель – принцип Даламбера, для чего ему нужно дополнительно к активным силам ввести силы инерции. Оба подхода являются справедливыми и дают правильное решение.
Рассмотрим, например, круговое движение тела, закрепленного на нити. С точки зрения неподвижного наблюдателя в системе xyдвижение тела по круговой траектории происходит под действием реакции нити, направленной к центру вращения и действующей в соответствии с законом:
R = ma,
где a = ω2 R- ускорение центра тяжести тела.
R - носит название центростремительной силы.
Для наблюдателя, находящегося в системе ξη, тело m не движется. Это возможно только потому, что на него действуют две силы R и U, находящиеся в равновесии. Сила инерции U называется в этом случае центробежной силой.
Для решения обратных задач динамики более удобным является второй подход, так как он приводит к рассмотрению условия равновесия сил. Это объясняет причину широкого использования в технических расчетах сил инерции.
Пример 1. Тело М совершает вращательное движение вокруг некоторой точки О. Такое движение можно осуществить разными способами, но всегда должна существовать связь, обуславливающая окружную траекторию точек тела. Эту связь можно осуществить, например, с помощью нити (3.2).
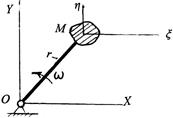
Рис. 3.2. Связь с помощью нити
Предположим, что телу М посредством толчка сообщен начальный импульс в направлении, касательном к окружной траектории. Требуется объяснить равномерное вращательное движение. Существование связи проявляется в виде реакции, т.е. в виде внешней силы, действующей на тело М. Эту силу должен принимать во внимание как инерциальный, так и неинерциальный наблюдатель. Но для неинерциального наблюдателя тело М неподвижно, т.к. его система отсчета xh жестко связана с телом. Это возможно лишь в том случае, если равнодействующая всех сил, приложенных к телу, равна нулю. Значит, кроме реакции, на тело действует еще одна сила, равная реакции связи, но противоположно направленная. Это сила инерции. Поскольку тело М неподвижно в неинерциальной системе отсчета xh, сила инерции представляется только одной составляющей — переносной силой инерции Ue. Для определения ее величины и направления нужно знать величину и направление переносного ускорения aеМ. При любом варианте выбора подвижной системы xh переносное ускорение совпадает с центростремительным ускорением центра тяжести тела М при его равномерном движении по окружной траектории.
На основании вышеизложенного определяются сила инерции
ue = - mw2r
и реакция связи
R = mw2r.
Для наблюдателя, находящегося в неподвижной системе отсчета xy, никаких сил инерции не существует, но зато тело М движется по окружной траектории и, следовательно, обладает ускорением. Единственная сила, приложенная к нему — реакция связи. Она и объясняет наличие ускорения. Действительно, реакция связи, осуществляемой нитью, может быть направлена только по нити к центру, что и обуславливает появление в этом направлении ускорения. Поскольку это ускорение всегда направлено к центру, оно называется центростремительным. Величина его, как известно из кинематики, равна w2r.
В приводимых объяснениях пока не ясна причина возникновения реакции связи. После начального толчка тело, двигаясь в направлении импульса, т.е. касательно к окружной траектории, растягивает нить. Это растяжение продолжается до тех пор, пока возникающая при этом сила упругой деформации нити не сообщит телу ускорение, необходимое для осуществления движения по окружности. Нить при этом, вообще говоря, увеличивает свою длину по сравнению с первоначальной. Но обычно предполагается, что связь достаточно жесткая и этой деформацией пренебрегают. Однако существование этой деформации принципиально важно для объяснения наблюдаемого движения.
Величину реакции связи можно определить исходя из того, что известно центростремительное ускорение центра тяжести тела М:
R = mw2r.
Эту реакцию иногда называют центростремительной силой, т.к. она обуславливает центростремительное ускорение. Природа центростремительной силы в упругой деформации связи. Неинерциальный наблюдатель, имеющий дело с равновесием сил, вторую силу, силу инерции, естественно, может называть центробежной силой, отчего она не перестает быть силой инерции.
Пример 2. Основываясь на вышеизложенном, объясним причины разрушения связей, в частности разрушение быстровращающихся маховиков и шлифовальных кругов.
Всякое вращательное движение связано с деформацией связи, причем, чем больше ускорение тела, тем больше деформация связи. Величина ускорения может быть какой угодно, а величина деформации не может превышать допустимую из условия прочности связи. Если начальный импульс будет слишком велик за счет сообщения очень большой скорости телу, то это приведет к очень большому ускорению в последующем вращательном движении. Это вытекает из того, что величина сообщенной телу скорости должна сохраниться и во вращательном движении, а это в случае достаточно жесткой связи возможно лишь за счет большой угловой скорости. Связь разрушится из-за несоответствия допустимой деформации и ускорения, обусловленного начальным импульсом.
Если большая скорость телу М сообщена путем постепенного увеличения угловой скорости, как это имеет место в случае быстровращающихся маховиков и шлифовальных кругов, разрушение их происходит из-за невозможности обеспечить требуемое ускорение посредством связи, обладающей ограниченной деформационной способностью.
Таким образом, не появление каких-то дополнительных сил является причиной разрушения маховиков и шлифовальных кругов, а, наоборот, отсутствие возможности обеспечить необходимую упругую силу посредством деформируемой связи.
Приведенное объяснение является точкой зрения инерциального наблюдателя, но вывод справедлив и для неинерциального, т.к. и в этом случае сила инерции является не причиной, а следствием возникающего движения с ускорением. Само движение возможно лишь при выполнении тех же условий, что и для инерциального наблюдателя.
Пример 3. Тело М помещено с возможность перемещения на прямолинейном рычаге 1, вращающимся с угловой скоростью w. Траектория движения центра тяжести тела М представляет некоторую кривую (рис. 3.3).
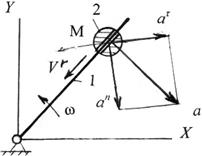
Рис. 3.3. Вращение на прямолинейном рычаге
Инерциальный наблюдатель в системе xy наблюдает движение по кривой с ускорением. Полное ускорение a может быть разложено на нормальное an, направленное внутрь кривой, и касательное at вдоль кривой. Сила, вызывающая ускорение a, есть реакция со стороны рычага 1. Так как в отсутствии сил трения направление реакции перпендикулярно рычагу, всегда можно указать направление полного ускорения a.
Неинерциальный наблюдатель, связанный с подвижной системой координат xh (рис.3.4), также наблюдает движение тела М и объясняет его действием реакцией R и силы инерции U.
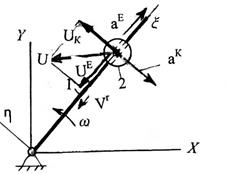
Рис. 3.4. Направление сил инерции
Поскольку наблюдаемое им движение происходит вдоль прямолинейного рычага, также должна быть направлена и результирующая сила. Сила инерции в данном случае представлена переносной и кориолисовой силами инерции. Переносное и кориолисово ускорения, определяемые по известным правилам, указаны на рис. 3.4.
3.4. Силы инерции в поступательном, вращательном
и сложном движении
Пусть тело находится в поступательном движении с ускорением. На каждую точку этого тела действуют равные и одинаково направленные силы инерции. Имеем систему равных и параллельных сил. Как известно из теоретической механики, такую систему сил можно привести к одной силе, приложенной в центре масс и равной
U = - maS .
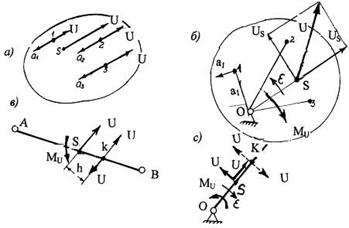
Рис. 3.5. Силы инерции в поступательном, вращательном и сложном движении
Пусть тело вращается вокруг точки О с угловой скоростью ω и угловым ускорением ε. На каждую точку этого тела действует сила инерции, которую можно представить состоящей из касательной и нормальной составляющих силы инерции. В теоретической механике доказывается, что такая система сил приводится к главному вектору и главному моменту сил инерции. Главный вектор сил инерции приложен в центре масс и вычисляется по формуле
U = - maS,
где aS – ускорение центра масс.
Главный момент сил инерции вычисляется по формуле
MU = - JS ε ,
где JS – момент инерции тела относительно оси, проходящей через центр масс перпендикулярно плоскости движения. Момент инерции вычисляется как интеграл вида:
JS = ∫ mi ρi2,
где ρi - расстояние от точек, образующих в совокупности данное тело, до центра масс – точки S. Момент инерции зависит как от массы, так и от формы тела, т.е. он определяет геометрию масс. Моменты инерции тел различной формы приводятся в справочниках. Для тела типа стержня
JS = mL2/ 12,
где L - длина стержня.
Для диска
JS = m R2,
где R - радиус диска.
При вращательном движении возможны следующие частные случаи.
1. Вращение вокруг центра масс. В таком случае OS = 0, следовательно U = 0, Mu = - JS ε.
2. Вращение с постоянной скоростью. В таком случае ε = 0, следовательно Mu = 0, U = - ma.
3. Вращение вокруг центра масс с постоянной скоростью. В таком случае U = 0, Mu = 0.
Сложное движение можно представить состоящим из поступательного вместе с центром масс и вращательного вокруг центра масс. При поступательном движении с ускорением возникает сила инерции U = - m aS, при вращательном движении вокруг центра масс возникает только момент сил инерции Mu = - JS ε. Таким образом, в сложном движении, как и во вращательном, имеются главный вектор сил инерции U и главный момент сил инерции Mu.
Силу и момент можно заменить одной силой. Приложим в точке К силы U и -U (рис.3.5в). Это не изменит состояния равновесия тела. Сила - U и сила U в точке S образует пару сил с моментом M = Uh. Если выбрать h из условия h = Mu / U, то момент M компенсирует момент Mu и останется одна сила U , приложенная в точке К. Для вращающегося тела, имеющего форму стержня длиной L, можно указать простой способ нахождения точки К. Разложим силу U на составляющие Uτ и Un и приложим в точке К две силы Uτ и - Uτ. Для компенсации Muнеобходимо, чтобы Uτ h = M =Mu. После соответствующих подстановок найдем :
H = L / 6, OK = 2 L/ 3 .
Силы инерции звена, совершающего пространственное движение, сводятся к главному вектору, вычисляемому, как и в плоском случае, по формуле U = - m aS, и главному моменту сил инерции, который находится на основании динамических уравнений Эйлера. Проекции главного момента на главные центральные оси инерции звена находятся из уравнений:
Mux = - Jx εx - ( Jz – Jy) ωyωz ;
Muy = - Jy εz - (Jx - Jz) ωzωx ;
Muz = - Jz εz - (Jy - Jx) ωxωy ,
где Jx, Jy, Jz — главные центральные моменты инерции звена;
ωч, ωy, ωz, εx, εy, εz, -проекции вектора угловой скорости и вектора углового ускорения на главные центральные оси инерции.
Для того чтобы перейти от проекций на оси, связанные с телом, к проекциям на оси xyz, можно воспользоваться матрицей перехода от подвижных осей к осям xyz.
3.5. Силовое исследование механизмов методами кинетостатики
В тихоходных механизмах динамические эффекты проявляются незначительно, поэтому усилия можно найти на основании статического расчета, приняв во внимание только движущую силу, силы тяжести, силу трения, силу полезного сопротивления. В быстроходных механизмах следует учитывать динамические эффекты. Проще всего это сделать, если воспользоваться принципом Даламбера. Для этого нужно ко всем внешним силам добавить силы инерции и рассматривать такую систему сил находящейся в равновесии. Такой подход называется методом кинетостатики.
Силы инерции можно рассчитать по приведенным выше формулам. Ускорения центров тяжести звеньев и угловые ускорения находятся на основании кинематического анализа при заданном движении ведущего звена. Кинетостатический расчет обычно выполняется в несколько этапов. На первом этапе силами трения пренебрегают. Определив реакции в кинематических парах, находят силы трения и повторяют расчет с учетом сил трения.
Все многочисленные методы расчета можно разделить на:графические, графоаналитические, аналитические. Графические и графоаналитические методы характеризуются относительной простотой реализации. Достоинство аналитических методов – возможность получения большого объема информации. Вследствие сложности вычислительных процедур расчеты выполняются на ЭВМ.
3.6. Условие статической определимости кинематической цепи
Чтобы решить задачу силового анализа методами статики необходимо, чтобы число уравнений было больше или равнялось числу неизвестных. Это условие носит название условия статической определимости системы.
В качестве неизвестных сил в кинематической цепи выступают силы реакции. Силы, действующие на каждое звено, можно свести к одной силе и моменту, приведя их к центру кинематической пары. Разложим силу и момент на составляющие вдоль выбранных осей пары, Получим три проекции силы и три проекции момента.
Вращательная кинематическая пара (рис. 3.6а) накладывает 5 условий связей, разрешая вращение только вокруг одной оси. Тогда под действием одной составляющей момента происходит движение звена, остальные составляющие момента и силы воспринимаются связями. Таким образом, во вращательной паре имеется 5 реакций связей.
Аналогичным образом можно установить, что в цилиндрической паре 4 реакции, в сферической – 3, в паре цилиндр на плоскости – 2, в паре шар на плоскости – 1.
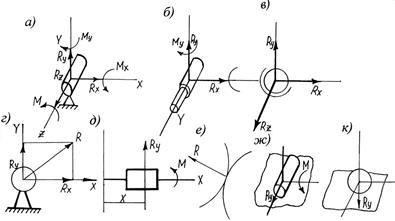
Рис. 3.6. Реакции в кинетических парах
Условие статической определимости пространственной кинематической цепи имеет вид:
6n = 5 p1 + 4 p2 + 3p3 + 2 p4 + p5 .
Это условие соответствует уравнению пространственной ассуровской группы.
Для плоской схемы во вращательной паре действуют момент и составляющие силы по осям x и y. Под действием момента происходит движение звена, силы воспринимаются связями. Таким образом, имеем две неизвестные реакции. В поступательной паре под действием составляющей силы вдоль оси x происходит движение звена, сила по оси y и момент воспринимаются связями, т.е. здесь также две неизвестные. В высшей паре действует только одна сила по нормали к поверхности в точке касания, т.е. имеется одна неизвестная.
Условие статической определимости плоской кинематической цепи
3n = 2 p1 + p2
совпадает с уравнением ассуровской группы. Отсюда можно сделать вывод, что ассуровские группы являются статически определимыми системами. Отдельно взятое звено с вращательными парами статически неопределимо, так как число уравнений меньше числа неизвестных. Два звена дают 6 уравнений при 6 неизвестных благодаря тому, что внутренние кинематические пары вносят в систему только две неизвестные. Из изложенного следует, что для выполнения силового исследования механизм нужно разложить на ассуровские группы и рассматривать их равновесие по отдельности.
3.7. Метод планов силы
Сущность метода планов сил рассмотрим на примере механизма 2-го класса с 2-мя диадами (рис. 3.7). Приложим к механизму все заданные внешние силы: момент силы полезного сопротивления MQ, силы тяжести звеньев Q, главные векторы и главные моменты сил инерции (силы инерции U и моменты сил инерции MU) , движущую силу . Движущую силу примем равной уравновешивающей силе Pур.
Под уравновешивающей силой понимают силу, уравновешивающую заданные внешние силы и силы инерции, определенные из условия равномерного вращения кривошипа. Вообще говоря, поскольку истинное движение отличается от равномерного вращения, постольку движущая сила отличается от уравновешивающей. Обычно уравновешивающую силу прикладывают в конце кривошипа перпендикулярно к нему. Уравновешивающая сила создает уравновешивающий момент относительно точки О.
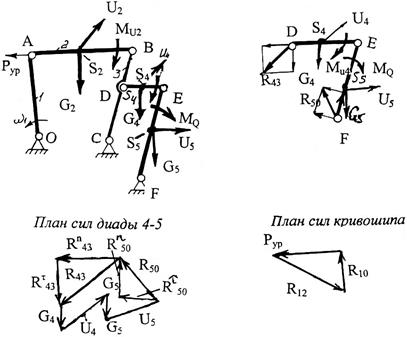
Рис 3.7. План сил шарнирного четырехзвенника
Задачей силового расчета является определение реакций в кинематических парах и уравновешивающей силы.
Выделим из механизма последнюю диаду, заменив отброшенные звенья реакциями. Условимся буквенные обозначения реакций снабжать индексами, руководствуясь правилом: первым пишется индекс, соответствующий номеру звена, на которое действует реакция, а вторым – индекс, соответствующий номеру звена, со стороны которого действует реакция.
Процедура расчета выполняется по шагам в следующем порядке.
1. Запишем уравнение равновесия диады в векторной форме:
R43 + G4 + U4 + U5 + G5 + R50 = 0 .
Это уравнение содержит две неизвестные реакции и пока не может быть решено.
2. Разложим реакции R43 и R50 на нормальные и касательные составляющие.
3. Запишем уравнение моментов всех сил, действующих на звено 4 и звено 5 в отдельности относительно точки Е.
M4E = 0 → R43τ, M5E = 0 → R50τ
В этих уравнениях по одной неизвестной R43τ и R50τ. Найдем эти неизвестные. Если они получаются со знаком минус, то это означает, что принятые направления найденных реакций следует заменить на обратные.
4. Возвратимся к исходному уравнению равновесия диады, переписав его в следующей форме:
R43n + R43τ + G4 + U4 + U5 + G5 + R50τ + R50τ = 0 .
Решим это уравнение графически. Для этого в выбранном масштабе построим многоугольник сил таким образом, чтобы неизвестные R43n и R50n были замыкающими этого многоугольника.
5. Для определения реакций во внутренней кинематической паре запишем уравнение равновесия звена 4
R43 + G4 + U4 + R45 = 0 .
В этом уравнении одно неизвестное - R45. Для его определения можно не строить отдельный векторный многоугольник, а выделить в многоугольнике диады вектора, входящие в это уравнение, и построить замыкающий вектор.
Перейдем к исследованию диады 2-3. Изобразим ее отдельно, заменив действие отброшенных звеньев реакциями. Расчет диады 2-3 выполняется точно также, как и диады 4-5.
Кривошип находится под действием уравновешивающей силы Pур, реакции со стороны 2-го звена R12, реакции со стороны стойки R10. Поскольку Pур и R12 приложены в одной точке, они дают равнодействующую, которая уравновешивается реакцией R10. Отсюда следует, что R10 направлена по звену. Уравнение равновесия кривошипа
P ур + R10 + R12 = 0 .
Из треугольника сил находятся реакции R10 и Pур.
3.8. Метод рычага Жуковского
Метод рычага Жуковского представляет геометрическую интерпретацию принципа возможных перемещений. Он применяется для плоских механизмов и позволяет определить уравновешивающую силу без предварительного определения реакций в кинематических парах. Принцип возможных перемещений (принцип Даламбера – Лагранжа) находит широкое применение в механике. Он формулируется следующим образом: работа всех активных сил и сил инерции на возможном перемещении системы равна нулю. Этот принцип эквивалентен закону сохранения энергии для механических систем. Он записывается в виде
ΣFK • δ rK = 0 , (3.3)
где в левой части стоит сумма скалярных произведений векторов сил FK на векторы возможных перемещений точек приложения этих сил δrK.
Разделим выражение (3.3) на δt:
ΣFK δrK / δt = ΣFk • Vk = Σ|FK | | VK | cos ( Fk • Vk) = 0.
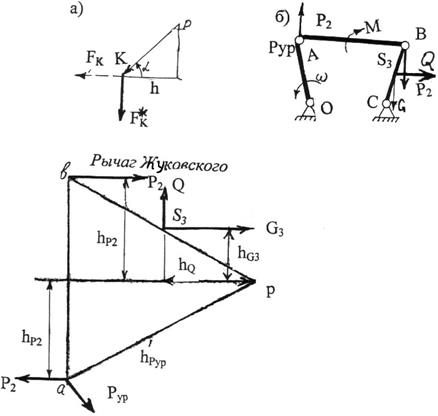
Рис 3.8. Метод рычага Жуковского
Рассмотрим элемент плана скоростей, на котором изображена скорость точки К . Приложим к точке К вектор FK*, изображающий силу FK,, повернутую на 90˚ относительно ее истинного направления. Из построения на рис. 3.8а следует:
h = pk cos α = VK cos α / kv= VK cos (FK , VK) / kv . (3.4)
Если рассматривать отрезок pk как рычаг, закрепленный в точке р, то сила FK* создает момент:
MK = FK* h = |FK* | |VK | cos (FK VK ) / kv . (3.5)
Из сравнения выражений (3.4) и (3.5) следует, что с точностью до множителя kv
ΣFK δrk / δt = ΣMK = 0 .
Полученный результат известен как теорема Жуковского:
Если в соответствующие точки плана скоростей механизма приложить все активные силы и силы инерции, повернутые на 90º в одну сторону, то сумма моментов этих сил относительно полюса плана скоростей, рассматриваемого как жесткий рычаг, равна нулю.
На рис.3.8б представлен пример использования теоремы Жуковского для определения уравновешивающей силы в шарнирном четырехзвеннике.
В этом примере для правильного учета момента М он заменен парой сил (P' = P") так, что M = P2' LAB. Уравновешивающая сила определяется из уравнения
Pур hур + P2'hp2' + P2 hp2" + G3 hG3 + Q hQ = 0 .
При составлении уравнения должно соблюдаться правило знаков: момент, действующий против часовой стрелки, - положительный, по часовой стрелке – отрицательный.
Можно повернуть план скоростей, а силы не поворачивать, результат будет тот же.
3.9. Аналитический метод силового исследования
Известно несколько аналитических методов силового исследования. Познакомимся с методом, в основе которого также лежит принцип возможных перемещений. Для шарнирного четырехзвенника, нагруженного только уравновешивающим моментом Мур и моментом сил полезного сопротивления MQ, уравнение равновесия имеет вид:
Mур δφ1 + MQ δφ3 = 0 ,
откуда следует
Mур = - MQ δφ3 / δφ1 . (3.6)
Задача сводится к чисто кинематической: нужно выразить δφ3 через δφ1 и подставить в уравнение (3.6). Зависимость δφ3 от δφ1 устанавливается при решении задачи о скоростях.
Точно также можно учитывать действие других сил. При одновременном приложении нескольких сил уравновешивающий момент равен сумме моментов, рассчитанных для отдельных сил. В этом проявляется принцип суперпозиции – независимости действия сил.
Аналитический метод, в отличие от графического, можно применять и для пространственных механизмов. Расчет, вследствие сложности расчетов, производится с использованием вычислительных машин.
3.10. Задача уравновешивания ротора
Ротором называется звено механизма, выполненное в виде тела вращения и установленное в опорах на стойке. В связи с ростом рабочих скоростей машин уравновешиванию роторов придается большое значение. Уравновешивание представляет ответственный этап при изготовлении машин. Качество машины во многом определяется ее уравновешенностью. В настоящее время строятся электродвигатели и турбомашины со скоростью вращения 100000 оборотов в минуту, центрифуги для получения биологических эмульсий со скоростью вращения до 600000 оборотов в минуту, отдельные детали в текстильных машинах вращаются со скоростью до 1000000 оборотов в минуту.
Рассмотрим следующий пример: пусть масса ротора 10 кг, угловая скорость ω = 1000 рад/с, эксцентриситет массы 0.0001 м (0.1 мм). При вращении ротора возникает сила инерции U = mω2R = 1000 н, т.е. в 10 раз больше, чем вес ротора.
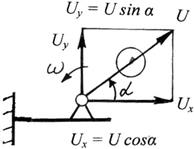
Рис 3.9. Действие неуравновешенного ротора на балку
Сила инерции передается на опоры в виде периодического воздействия. Пусть, например, неуравновешенный ротор закреплен на консольной балке (рис. 3.9). Разложим силу инерции U на составляющие Ux и Uy. Составляющая Ux из-за большой жесткости балки в направлении оси X не опасна, составляющая Uy вызывает колебания балки. Если частота вынужденных колебаний равна частоте свободных колебаний или ей кратна, может возникнуть резонанс. Резонанс характеризуется резким возрастанием амплитуды колебаний, что может привести к поломке или, в лучшем случае, будет проявляться в виде вибраций оборудования, здания и т.д.. Неуравновешенность может появиться также из-за неточности изготовления, пороков в материале и т. д. Задача конструктора – не допустить ошибок при проектировании ротора.
3.11. Статическая неуравновешенность ротора
Статической называется неуравновешенность, возникающая от того, что главная центральная ось инерции ротора проходит параллельно оси вращения. Свое название она получила потому, что она может быть обнаружена проведением статических испытаний. Рассмотрим простейшую схему статически неуравновешенного ротора (рис. 3.10 ). Подсчитаем силу инерции, развиваемую массой m
U = m ω2 e.
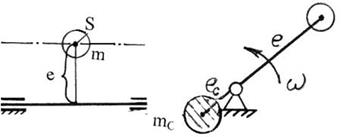
Рис 3.10. Схема статически неуравновешенного ротора
Силу инерции при угловой скорости ω = 1 называют дисбалансом:
D = U = m e .
Дисбаланс – произведение массы на эксцентриситет, его размерность гсм.
Задача уравновешивания – изменить распределение масс с тем, чтобы перевести центр масс на ось вращения. Тогда главная центральная ось инерции и ось вращения совпадут. Этого можно добиться, если использовать корректирующую массу mc, расположить ее на расстоянии ес противоположно массе m так, чтобы она развивала силу инерции Uc = - U или Dc = - D. Отсюда следует, что для статической уравновешенности необходимо, чтобы геометрическая сумма дисбалансов равнялась нулю
(Dc + D = 0).
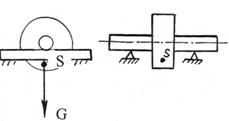
Рис 3.11. Балансировка ротора на параллелях
На практике статическое уравновешивание выполняют на балансировочных станках. Обычно используются балансировочные параллели (рис. 3.11) Установленный на них ротор под действием момента сил тяжести совершает колебания относительно положения устойчивого равновесия, при котор
Дата добавления: 2016-10-18; просмотров: 6456;











