Общее уравнение динамики
Общее уравнение динамики для системы с любыми связями (объединенный принцип Даламбера-Лагранжа или общее уравнение механики):
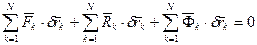 , (229)
, (229)
где 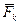 – активная сила, приложенная к
– активная сила, приложенная к 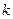 -ой точке системы;
-ой точке системы; 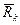 – сила реакции связей;
– сила реакции связей; 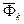 – сила инерции точки;
– сила инерции точки; 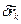 – возможное перемещение.
– возможное перемещение.
Оно в случае равновесия системы при обращении в нуль всех сил инерции точек системы переходит в принцип возможных перемещений. Обычно его применяют для систем с идеальными связями, для которых выполняется условие
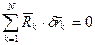
В этом случае (229) принимает одну из форм:
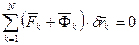 ,
,
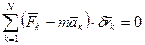 ,
,
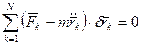 . (230)
. (230)
Таким образом, согласно общему уравнению динамики, в любой момент движения системы с идеальными связями сумма элементарных работ всех активных сил и сил инерции точек системы равна нулю на любом возможном перемещении системы, допускаемом связями.
Общему уравнению динамики можно придать другие, эквивалентные формы. Раскрывая скалярное произведение векторов, его можно выразить в виде
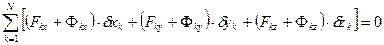 ,
,
где 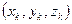 – координаты
– координаты 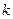 -ой точки системы. Учитывая, что проекции сил инерции на оси координат через проекции ускорений на эти оси выражаются соотношениями
-ой точки системы. Учитывая, что проекции сил инерции на оси координат через проекции ускорений на эти оси выражаются соотношениями
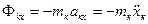 ,
,
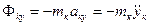 ,
,
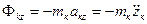 ,
,
общему уравнению динамики можно придать форму
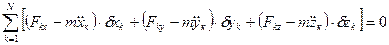 .
.
В этом виде его называют общим уравнением динамики в аналитической форме.
При использовании общего уравнения динамики необходимо уметь вычислять элементарную работу сил инерции системы на возможных перемещениях. Для этого применяются соответствующие формулы для элементарной работы, полученные для обычных сил. Рассмотрим их применение для сил инерции твердого тела в частных случаях его движения.
При поступательном движении.В этом случае тело имеет три степени свободы и вследствие наложенных связей может совершать только поступательное движение. Возможные перемещения тела, которые допускают связи, тоже являются поступательными.
Силы инерции при поступательном движении приводятся к равнодействующей 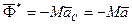 . Для суммы элементарных работ сил инерции на поступательном возможном перемещении тела получим
. Для суммы элементарных работ сил инерции на поступательном возможном перемещении тела получим
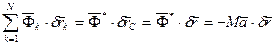 ,
,
где 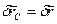 – возможное перемещение центра масс и любой точки тела, так как поступательное возможное перемещение у всех точек тела одинаково: одинаковы и ускорения, т. е.
– возможное перемещение центра масс и любой точки тела, так как поступательное возможное перемещение у всех точек тела одинаково: одинаковы и ускорения, т. е. 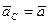 .
.
При вращении твердого тела вокруг неподвижной оси. Тело в этом случае имеет одну степень свободы. Оно может вращаться вокруг неподвижной оси 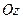 . Возможное перемещение, которое допускается наложенными связями, является тоже поворотом тела на элементарный угол
. Возможное перемещение, которое допускается наложенными связями, является тоже поворотом тела на элементарный угол 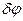 вокруг неподвижной оси.
вокруг неподвижной оси.
Силы инерции, приведенные к точке 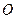 на оси вращения, сводятся к главному вектору
на оси вращения, сводятся к главному вектору 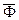 и главному моменту
и главному моменту 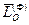 . Главный вектор сил инерции приложен к неподвижной точке, и его элементарная работа на возможном перемещении равна нулю. У главного момента сил инерции не равную нулю элементарную работу совершит только его проекция на ось вращения
. Главный вектор сил инерции приложен к неподвижной точке, и его элементарная работа на возможном перемещении равна нулю. У главного момента сил инерции не равную нулю элементарную работу совершит только его проекция на ось вращения 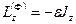 . Таким образом, для суммы работ сил инерции на рассматриваемом возможном перемещении имеем
. Таким образом, для суммы работ сил инерции на рассматриваемом возможном перемещении имеем
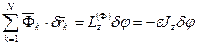 ,
,
если угол 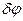 сообщить в направлении дуговой стрелки углового ускорения
сообщить в направлении дуговой стрелки углового ускорения 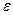 .
.
При плоском движении. Связи, наложенные на твердое тело, допускают в этом случае только плоское возможное перемещение. В общем случае оно состоит из поступательного возможного перемещения вместе с полюсом, за который выберем центр масс, и поворота на элементарный угол 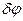 вокруг оси
вокруг оси 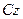 , проходящей через центр масс и перпендикулярной плоскости, параллельно которой может совершать тело плоское движение.
, проходящей через центр масс и перпендикулярной плоскости, параллельно которой может совершать тело плоское движение.
Так как силы инерции при плоском движении твердого тела можно привести к главному вектору 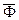 и главному моменту
и главному моменту 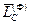 (если за центр приведения выбрать центр масс), то сумма элементарных работ сил инерции на плоском возможном перемещении сведется к элементарной работе отавною вектора сил инерции
(если за центр приведения выбрать центр масс), то сумма элементарных работ сил инерции на плоском возможном перемещении сведется к элементарной работе отавною вектора сил инерции 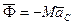 на возможном перемещении центра масс и элементарной работе главного момента сил инерции на элементарном поворотном перемещении вокруг оси
на возможном перемещении центра масс и элементарной работе главного момента сил инерции на элементарном поворотном перемещении вокруг оси 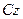 , проходящей через центр масс. При этом не равную нулю элементарную работу может совершить только проекция главного момента сил инерции на ось
, проходящей через центр масс. При этом не равную нулю элементарную работу может совершить только проекция главного момента сил инерции на ось 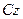 , т.е.
, т.е. 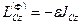 . Таким образом, в рассматриваемом случае имеем
. Таким образом, в рассматриваемом случае имеем
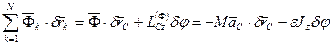 ,
,
если поворот на элементарный угол 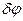 направить по дуговой стрелке для
направить по дуговой стрелке для 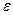 .
.
ЛЕКЦИЯ № 10
Дата добавления: 2017-09-01; просмотров: 1971;











