Уравнения Лагранжа второго рода

Уравнения Лагранжа можно рассматривать как алгоритм получения дифференциальных уравнений движения системы, т.е. дифференциальных уравнений относительно обобщенных координат.

Уравнения Лагранжа первого рода для голономной механической системы с 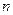степенями свободы, на которую наложены идеальные связи имеют вид:

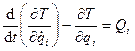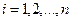, , (231)

где 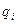– обобщенные координаты; величина 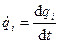– обобщенная скорость; 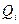–обобщенная сила, отнесенная к обобщенной координате 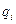; 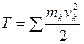– кинетическая энергия системы.

Число уравнений Лагранжа равно числу степеней свободы системы.

При составлении уравнений Лагранжа можно рекомендовать следующий порядок операций.

1. Вычислить кинетическую энергию системы в ее движении относительно инерциальной системы отсчета.

2. Выбрав обобщенные координаты, число которых равно числу степеней свободы системы, преобразовать кинетическую энергию к обобщенным координатам.

3. Выполнить операции дифференцирования кинетической энергии, предусмотренные уравнениями Лагранжа.

4. Вычислить одним из способов, указанных в пункте 3.5.6. обобщенные силы системы.

5. Приравнять величины левой и правой частей, входящих в уравнения Лагранжа.