Возможные перемещения

Для одной точки возможным (виртуальным) перемещением называется такое бесконечно милое (элементарное) мысленное перемещение, которое допускается в рассматриваемый момент времени наложенными на точку связями. Для возможного перемещения не требуется времени на его совершение. Это мысленное перемещение, которое могла бы совершить точка при наложенных на нее связях в рассматриваемый момент времени. В отличие от элементарного (бесконечно малого) действительного перемещения точки 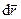, которое совершает точка за время 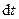под действием приложенных сил при заданных начальных условиях и наложенных связях, возможное перемещение 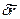определяется только связями в данный момент. 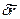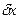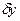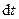Проекции возможного перемещения на оси координат, или вариации координат, обозначают , , , а проекции элементарного действительного перемещения на оси координат, или дифференциалы координат при изменении времени на обозначают , , .

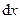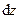Возможных перемещений у точки в момент времени 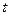бесконечно много. Если, например, точка движется по поверхности, все допускаемые связью (поверхностью) возможные перемещения как отрезки бесконечно малой длины расположатся в касательной плоскости к поверхности в точке, в которой находится рассматриваемая материальная точка в данный момент времени.

Возможное перемещение 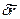, как и действительное 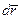, является вектором и потому всегда изображается направленным прямолинейным отрезком.

Возможным перемещением системы называют любую совокупность возможных перемещений точек системы. В общем случае система может иметь несколько и даже бесконечно много возможных перемещений. Вследствие уравнений связей, наложенных на систему, не все возможные перемещения являются независимыми. Число независимых возможных перемещений называют числом степеней свободы системы.

Свободная точка имеет три степени свободы. В этом случае возможные перемещения (вариации) 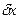, , 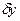(или выраженные через вариации каких-либо других координат) являются независимыми.