Решение задач динамики
Пример 7.  На вертикальном участке
На вертикальном участке 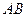 трубы (рис. 55) на груз
трубы (рис. 55) на груз 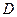 массой
массой 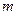 действуют сила тяжести и сила сопротивления
действуют сила тяжести и сила сопротивления 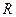 ; расстояние от точки
; расстояние от точки 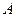 , где
, где 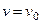 , до точки
, до точки 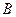 равно
равно 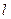 . На наклонном участке
. На наклонном участке 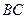 на груз действуют сила тяжести, сила трения скольжения
на груз действуют сила тяжести, сила трения скольжения 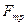 с коэффициентом трения
с коэффициентом трения 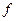 переменная сила
переменная сила 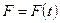 , заданная в ньютонах.
, заданная в ньютонах.
 Дано:
Дано: 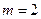 кг,
кг, 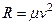 , где
, где 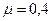 кг/м,
кг/м, 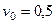 м/с,
м/с, 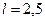 м,
м, 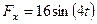 ,
, 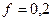 .
.
Определить: 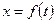 на участке
на участке 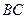 .
.
Решение:
1. Рассмотрим движение груза на участке 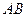 , считая груз материальной точкой. Изображаем груз (в произвольном положении) и действующие на него силы
, считая груз материальной точкой. Изображаем груз (в произвольном положении) и действующие на него силы 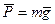 и
и 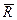 . Проводим ось
. Проводим ось 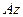 и составляем дифференциальное уравнение движения груза в проекции на эту ось:
и составляем дифференциальное уравнение движения груза в проекции на эту ось:
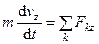 , или,
, или, 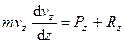 . (232)
. (232)
Далее находим 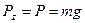 ,
, 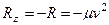 . Подчеркиваем, что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что
. Подчеркиваем, что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что 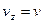 , получим
, получим
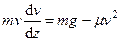 , или
, или 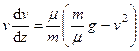 . (233)
. (233)
Введем для сокращения записей обозначения:
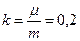 м–1,
м–1, 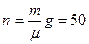 м2/с2, (234)
м2/с2, (234)
где при подсчете принято  м2/с2. Тогда уравнение (233) можно представить в виде:
м2/с2. Тогда уравнение (233) можно представить в виде:
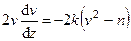 . (235)
. (235)
Разделяя в уравнении (235) переменные, а затем беря от обеих частей интегралы, получим
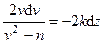 и
и 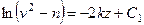 . (236)
. (236)
По начальным условиям при 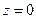
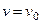 , что дает
, что дает 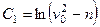 и из равенства (236) находим
и из равенства (236) находим 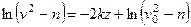 или
или  . Отсюда
. Отсюда
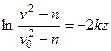 и
и 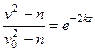 .
.
В результате находим:
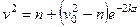 . (237)
. (237)
Полагая в равенстве (237) 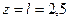 м, и заменяя
м, и заменяя 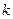 и
и 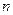 их значениями (234), определим скорость ив груза в точке
их значениями (234), определим скорость ив груза в точке 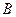 (
( 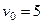 м/с, число
м/с, число 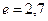 ):
):
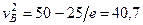 и
и 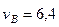 м/с. (238)
м/с. (238)
2. Рассмотрим теперь движение груза на участке 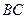 . Найденная скорость
. Найденная скорость 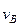 будет для движения на этом участке начальной скоростью (
будет для движения на этом участке начальной скоростью ( 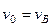 ). Изображаем груз (в произвольном положении) и действующие на него силы
). Изображаем груз (в произвольном положении) и действующие на него силы 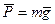 ,
, 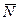 ,
, 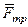 и
и 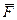 . Проведем из точки
. Проведем из точки 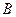 оси
оси 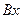 и
и 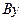 и составим дифференциальное уравнение движения груза в проекции на ось
и составим дифференциальное уравнение движения груза в проекции на ось 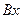 :
:
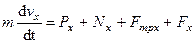 ,
,
или
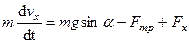 , (239)
, (239)
где 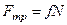 . Для определения
. Для определения 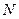 составим уравнение в проекции на ось
составим уравнение в проекции на ось 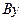 . Так как
. Так как 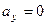 , получим
, получим 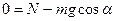 , откуда
, откуда 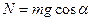 . Следовательно,
. Следовательно, 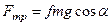 . Кроме того,
. Кроме того, 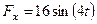 и уравнение (239) примет вид:
и уравнение (239) примет вид:
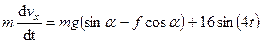 . (240)
. (240)
Разделив обе части равенства на 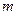 , вычислив
, вычислив 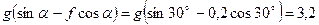 и
и  , подставим эти значения в (9). Тогда получим:
, подставим эти значения в (9). Тогда получим:
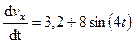 . (241)
. (241)
Умножая обе части уравнения (241) на 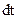 и интегрируя, найдем:
и интегрируя, найдем:
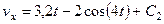 . (242)
. (242)
Будем теперь отсчитывать время от момента, когда груз находится в точке 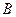 , считая в этот момент
, считая в этот момент 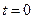 . Тогда при
. Тогда при 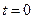
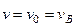 , где
, где 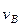 дается равенством (238). Подставляя эти величины в (242), получим
дается равенством (238). Подставляя эти величины в (242), получим
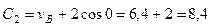 .
.
При найденном значении 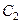 уравнение (242) дает:
уравнение (242) дает:
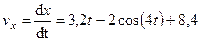 . (243)
. (243)
Умножая здесь обе части на 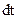 и снова интегрируя, найдем
и снова интегрируя, найдем
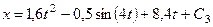 . (244)
. (244)
Так как при 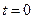
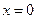 , то
, то 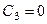 и окончательно искомый закон движения груза будет
и окончательно искомый закон движения груза будет
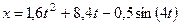 . (245)
. (245)
где 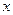 – в метрах,
– в метрах, 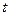 – в секундах.
– в секундах.
Ответ: 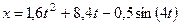 ,
, 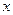 – в метрах,
– в метрах, 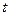 – в секундах.
– в секундах.

 Пример 8. В центре тяжести
Пример 8. В центре тяжести 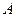 тележки массой
тележки массой 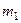 , движущейся по гладкой горизонтальной плоскости, укреплен невесомый стержень
, движущейся по гладкой горизонтальной плоскости, укреплен невесомый стержень 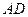 длиной
длиной 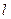 с грузом
с грузом 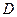 массой
массой 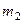 на конце (рис. 56). В момент времени
на конце (рис. 56). В момент времени 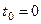 , когда скорость тележки
, когда скорость тележки 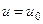 , стержень
, стержень 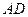 начинает вращаться вокруг оси
начинает вращаться вокруг оси 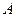 по закону
по закону 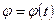 .
.
Дано: 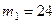 кг,
кг, 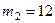 кг,
кг, 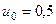 м/с,
м/с, 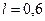 м,
м, 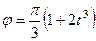 рад, где
рад, где 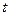 – в секундах.
– в секундах.
Определить: закон изменения скорости тележки 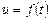 .
.
Решение:
1. Рассмотрим механическую систему, состоящую из тележки и груза 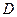 , в произвольном положении (рис. 56). Изобразим действующие на систему внешние силы: силы тяжести
, в произвольном положении (рис. 56). Изобразим действующие на систему внешние силы: силы тяжести 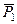 ,
, 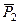 и реакции плоскости
и реакции плоскости 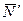 ,
, 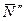 . Проведем координатные оси
. Проведем координатные оси 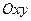 так, чтобы ось
так, чтобы ось 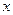 была горизонтальна.
была горизонтальна.
Чтобы определить 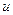 , воспользуемся теоремой об изменении количества движения системы
, воспользуемся теоремой об изменении количества движения системы 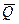 в проекции на ось
в проекции на ось 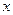 . Так как все действующие на систему внешние силы вертикальны (рис. 56), то
. Так как все действующие на систему внешние силы вертикальны (рис. 56), то 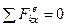 и теорема дает
и теорема дает
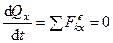 , откуда
, откуда 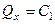 . (246)
. (246)
Для рассматриваемой механической системы 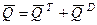 , где
, где 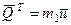 и
и 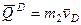 – количества движения тележки и груза
– количества движения тележки и груза 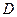 соответственно (
соответственно ( 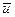 – скорость тележки,
– скорость тележки, 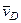 – скорость груза по отношению к осям
– скорость груза по отношению к осям 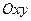 ). Тогда из равенства (246) следует, что
). Тогда из равенства (246) следует, что
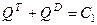 или
или 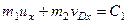 . (247)
. (247)
2. Определение 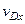 . Рассмотрим движение груза
. Рассмотрим движение груза 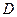 как сложное, считая его движение по отношению к тележке относительным (это движение, совершаемое при вращении стержня
как сложное, считая его движение по отношению к тележке относительным (это движение, совершаемое при вращении стержня 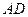 вокруг оси
вокруг оси 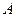 ), а движение самой тележки – переносным. Тогда
), а движение самой тележки – переносным. Тогда 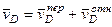 и
и
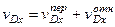 . (248)
. (248)
Но 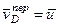 и, следовательно,
и, следовательно, 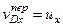 . Вектор
. Вектор 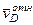 направлен перпендикулярно стержню и численно
направлен перпендикулярно стержню и численно 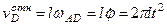 .
.
Изобразив этот вектор на рис. 56 с учетом знака 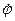 , найдем, что
, найдем, что 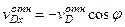 . Окончательно из равенства (248) получим
. Окончательно из равенства (248) получим
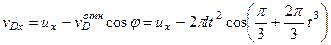 . (249)
. (249)
(В данной задаче величину 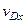 можно еще найти другим путем, определив абсциссу
можно еще найти другим путем, определив абсциссу 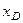 груза
груза 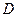 , для которой, как видно из рис. 56, получим
, для которой, как видно из рис. 56, получим 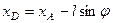 , тогда
, тогда 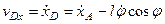 , где
, где 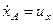 ,
, 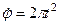 .)
.)
3. При найденном значении 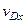 равенство (247), если учесть, что
равенство (247), если учесть, что 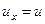 , примет вид
, примет вид
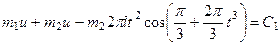 . (250)
. (250)
Постоянную интегрирования 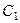 определим по начальным условиям: при
определим по начальным условиям: при 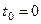 ,
, 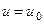 . Подстановка этих величин в уравнение (250) дает
. Подстановка этих величин в уравнение (250) дает 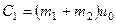 и тогда из (250) получим:
и тогда из (250) получим:
 .
.
Отсюда находим следующую зависимость скорости и тележки от времени
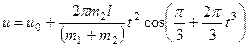 . (251)
. (251)
Подставив сюда значения соответствующих величин, находим искомую зависимость и от 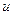 от
от 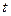 :
:
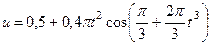 . (252)
. (252)
Ответ: 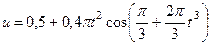
Пример 9. Однородная горизонтальная платформа (прямоугольная со сторонами 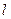 и
и 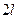 ), имеющая массу
), имеющая массу 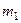 , жестко скреплена с вертикальным валом и вращается вместе с ним вокруг оси
, жестко скреплена с вертикальным валом и вращается вместе с ним вокруг оси 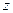 с угловой скоростью
с угловой скоростью 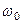 (рис. 57,а). В момент времени
(рис. 57,а). В момент времени 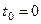 на вал начинает действовать вращающий момент
на вал начинает действовать вращающий момент 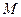 , направленный противоположно
, направленный противоположно 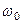 ; одновременно груз
; одновременно груз 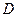 массой
массой 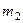 , находящийся в желобе
, находящийся в желобе 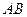 в точке
в точке 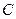 , начинает двигаться по желобу (под действием внутренних сил) по закону
, начинает двигаться по желобу (под действием внутренних сил) по закону 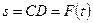 .
.
Дано: 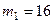 кг,
кг,  кг,
кг, 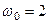 с–1,
с–1, 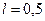 м,
м, 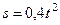 (где
(где 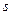 в метрах,
в метрах, 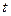 – в секундах),
– в секундах), 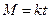 , где
, где 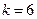
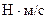 .
.
Определить: закон изменения угловой скорости платформы 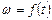 .
.
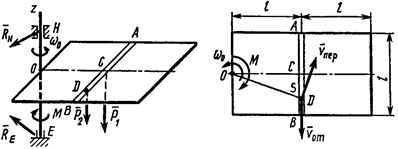
а) б)
Рис. 57
Решение:
1. Рассмотрим механическую систему, состоящую из платформы и груза 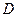 . Для определения
. Для определения 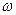 применим теорему об изменении кинетического момента системы относительно оси
применим теорему об изменении кинетического момента системы относительно оси 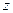 :
:
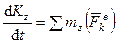 . (253)
. (253)
Изобразим действующие на систему внешние силы: силы тяжести 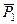 ,
, 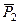 и реакции
и реакции 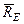 ,
, 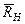 и вращающий момент
и вращающий момент 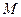 . Так как силы
. Так как силы 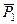 и
и 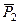 параллельны оси
параллельны оси 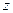 , а реакции
, а реакции 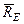 и
и 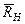 эту ось пересекают, то их моменты относительно оси
эту ось пересекают, то их моменты относительно оси 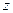 равны нулю. Тогда, считая для момента положительным направление против хода часовой стрелки, получим
равны нулю. Тогда, считая для момента положительным направление против хода часовой стрелки, получим 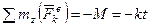 и уравнение (253) примет такой вид:
и уравнение (253) примет такой вид:
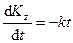 . (254)
. (254)
Умножая обе части этого уравнения на 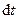 и интегрируя, получим
и интегрируя, получим
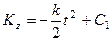 . (255)
. (255)
Для рассматриваемой механической системы
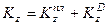 , (256)
, (256)
где 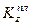 и
и 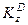 – кинетические моменты платформы и груза
– кинетические моменты платформы и груза 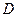 соответственно.
соответственно.
2. Определение 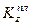 . Так как платформа вращается вокруг оси
. Так как платформа вращается вокруг оси 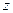 , то
, то 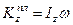 . Значение
. Значение 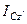 найдем по теореме Гюйгенса:
найдем по теореме Гюйгенса: 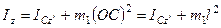 (
( 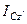 – момент инерции относительно оси
– момент инерции относительно оси 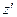 , параллельной оси
, параллельной оси 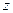 и проходящей через центр
и проходящей через центр 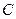 платформы).
платформы).
Но, как известно,
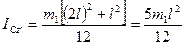 .
.
Тогда
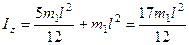 .
.
Следовательно,
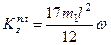 . (257)
. (257)
3. Для определения 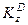 обратимся к рис. 57,б и рассмотрим движение груза
обратимся к рис. 57,б и рассмотрим движение груза 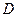 как сложное, считая его движение по платформе относительным, а вращение самой платформы вокруг оси
как сложное, считая его движение по платформе относительным, а вращение самой платформы вокруг оси 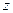 переносным движением. Тогда абсолютная скорость груза
переносным движением. Тогда абсолютная скорость груза 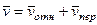 . Так как груз
. Так как груз 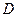 движется по закону
движется по закону 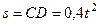 , то
, то 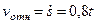 ; изображаем вектор
; изображаем вектор 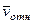 на рис. 57,б с учетом знака
на рис. 57,б с учетом знака 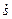 (при
(при 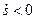 направление
направление 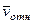 было бы противоположным). Затем, учитывая направление
было бы противоположным). Затем, учитывая направление 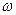 , изображаем вектор
, изображаем вектор 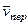 (
( 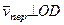 ); численно
); численно 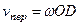 . Тогда, по теореме Вариньона,
. Тогда, по теореме Вариньона,
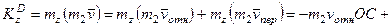
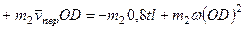 . (258)
. (258)
Из рис. 57,б видно, что 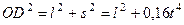 . Подставляя эту величину в равенство (6), находим
. Подставляя эту величину в равенство (6), находим 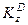 .
.
4. Подставив значения 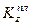 и
и 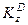 из (257) и (258) в равенство (256), получим с учетом данных задачи:
из (257) и (258) в равенство (256), получим с учетом данных задачи:
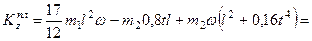
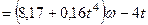 . (259)
. (259)
Тогда уравнение (255), где 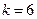 , примет вид
, примет вид
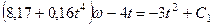 . (260)
. (260)
Постоянную интегрирования определяем по начальным условиям: при 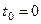 ,
, 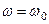 . Получим
. Получим 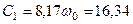 . При этом значении
. При этом значении 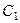 из уравнения (260) находим искомую зависимость
из уравнения (260) находим искомую зависимость 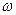 от
от 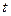 :
:
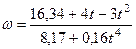 . (261)
. (261)
Ответ: 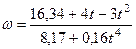 с–1, где
с–1, где 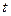 – в секундах.
– в секундах.
Пример 10. Механическая система (рис. 58) состоит из сплошного однородного цилиндрического катка 1, подвижного блока 2, ступенчатого шкива 3 с радиусами ступеней 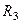 и
и 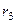 и
и  радиусом инерции относительно оси вращения
радиусом инерции относительно оси вращения  , блока 4 и груза 5 (коэффициент трения груза о плоскость равен
, блока 4 и груза 5 (коэффициент трения груза о плоскость равен 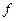 ). Тела системы соединены нитями, намотанными на шкив 3. К центру
). Тела системы соединены нитями, намотанными на шкив 3. К центру 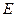 блока 2 прикреплена пружина с коэффициентом жесткости
блока 2 прикреплена пружина с коэффициентом жесткости 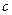 ; ее начальная деформация равна нулю. Система приходит в движение из состояния покоя под действием силы
; ее начальная деформация равна нулю. Система приходит в движение из состояния покоя под действием силы 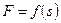 , зависящей от перемещения
, зависящей от перемещения 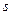 точки ее приложения. На шкив 3 при движении действует постоянный момент
точки ее приложения. На шкив 3 при движении действует постоянный момент 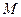 сил сопротивления.
сил сопротивления.
 Дано:
Дано:  кг,
кг, 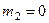 кг,
кг, 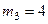 кг,
кг, 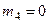 кг,
кг, 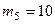 кг,
кг, 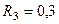 м,
м, 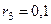 м,
м, 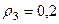 м,
м, 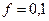 ,
, 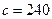 Н/м,
Н/м, 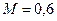
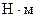 ,
, 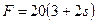 Н,
Н, 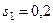 м.
м.
Определить: 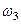 в тот момент времени, когда
в тот момент времени, когда 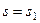 .
.
Решение:
1. Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 1, 3, 5 и невесомых тел 2, 4, соединенных нитями. Изобразим действующие на систему внешние силы: активные 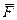 ,
, 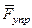 ,
, 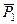 ,
, 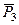 ,
,  , реакции
, реакции 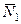 ,
, 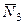 ,
, 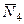 ,
, 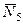 , натяжение нити
, натяжение нити 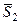 , силы трения
, силы трения 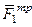 ,
, 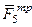 и момент
и момент 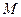 .
.
Для определения 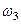 воспользуемся теоремой об изменении кинетической энергии:
воспользуемся теоремой об изменении кинетической энергии:
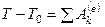 . (262)
. (262)
2. Определяем 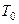 и
и 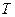 . Так как в начальный момент система находилась в покое, то
. Так как в начальный момент система находилась в покое, то 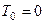 . Величина
. Величина 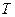 равна сумме энергий всех тел системы:
равна сумме энергий всех тел системы:
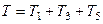 . (263)
. (263)
Учитывая, что тело 1 движется плоскопараллельно, тело 5 – поступательно, а тело 3 вращается вокруг неподвижной оси, получим
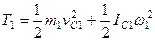 ,
,
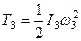 ,
,
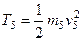 , (264)
, (264)
Все входящие сюда скорости надо выразить через искомую 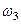 . Для этого предварительно заметим, что
. Для этого предварительно заметим, что  , где
, где 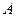 – любая точка обода радиуса
– любая точка обода радиуса 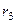 шкива 3 и что точка
шкива 3 и что точка  – мгновенный центр скоростей катка 1, радиус которого обозначим
– мгновенный центр скоростей катка 1, радиус которого обозначим 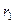 . Тогда
. Тогда
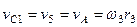 ,
, 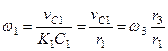 . (265)
. (265)
Кроме того, входящие в (3) моменты инерции имеют значения
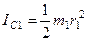 ,
, 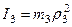 . (266)
. (266)
Подставив все величины (265) и (266) в равенства (264), а затем, используя равенство (263), получим окончательно
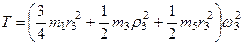 . (267)
. (267)
3. Найдем сумму работ всех действующих внешних сил при перемещении, которое будет иметь система, когда центр катка 1 пройдет путь 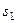 . Введя обозначения:
. Введя обозначения: 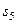 – перемещение груза 5 (
– перемещение груза 5 ( 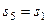 ),
), 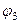 – угол поворота шкива 3,
– угол поворота шкива 3, 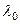 и
и  – начальное и конечное удлинения пружины, получим
– начальное и конечное удлинения пружины, получим
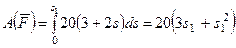 ,
,
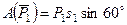 ,
,
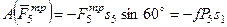 ,
,
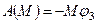 ,
,
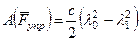 .
.
Работы остальных сил равны нулю, т.к. точки  и
и 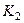 , где приложены силы
, где приложены силы 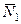 ,
, 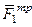 и
и 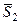 – мгновенные центры скоростей; точки, где приложены силы
– мгновенные центры скоростей; точки, где приложены силы 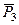 ,
,  и
и 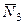 – неподвижны; а сила
– неподвижны; а сила 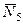 – перпендикулярна перемещению груза.
– перпендикулярна перемещению груза.
 По условиям задачи,
По условиям задачи, 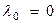 . Тогда
. Тогда 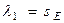 , где
, где 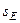 – перемещение точки
– перемещение точки 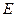 (конца пружины). Величины
(конца пружины). Величины 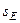 и
и 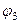 надо выразить через заданное перемещение
надо выразить через заданное перемещение 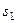 . Для этого учтем, что зависимость между перемещениями здесь такая же, как и между соответствующими скоростями. Тогда, так как
. Для этого учтем, что зависимость между перемещениями здесь такая же, как и между соответствующими скоростями. Тогда, так как 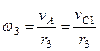 (равенство
(равенство 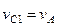 уже отмечалось), то и
уже отмечалось), то и  .
.
 Из рис. 59 видно, что
Из рис. 59 видно, что 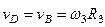 , а так как точка
, а так как точка 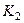 является мгновенным центром скоростей для блока 2 (он как бы «катится» по участку нити
является мгновенным центром скоростей для блока 2 (он как бы «катится» по участку нити 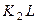 ), то
), то 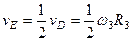 ; следовательно, и
; следовательно, и 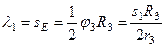 . При найденных значениях
. При найденных значениях 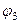 и
и  для суммы вычисленных работ получим
для суммы вычисленных работ получим
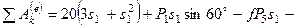
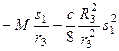 . (268)
. (268)
Подставляя выражения (267) и (268) в уравнение (262) и учитывая, что 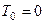 , придем к равенству
, придем к равенству
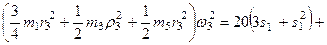
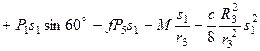 . (269)
. (269)
Из равенства (269), подставив в него числовые значения заданных величин, найдем искомую угловую скорость 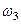 .
.
Ответ: 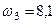 с–1.
с–1.
Пример 11. Механическая система (рис. 60) состоит из обмотанных нитями блока 1 радиуса 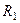 и ступенчатого шкива 2 (радиусы ступеней
и ступенчатого шкива 2 (радиусы ступеней 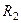 и
и  , радиус инерции относительно оси вращения
, радиус инерции относительно оси вращения 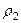 ), и из грузов 3 и 4, прикрепленных к этим нитям. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом
), и из грузов 3 и 4, прикрепленных к этим нитям. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом 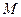 , приложенной к блоку 1.
, приложенной к блоку 1.
Дано: 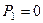 Н,
Н, 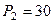 Н,
Н, 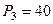 Н,
Н, 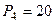 Н,
Н, 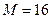
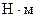 ,
, 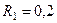 м,
м, 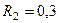 м,
м, 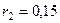 м;
м; 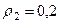 м.
м.
Определить: ускорение груза 3, пренебрегая трением.
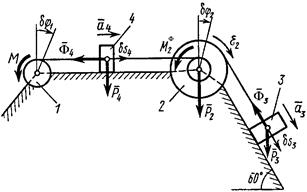
Рис. 60
Решение:
1. Рассмотрим движение механической системы, состоящей из тел 1, 2, 3, 4, соединенных нитями. Система имеет одну степень свободы. Связи, наложенные на эту систему, – идеальные.
Для определения 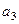 применим общее уравнение динамики:
применим общее уравнение динамики:
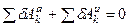 , (270)
, (270)
где 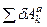 – сумма элементарных работ активных сил;
– сумма элементарных работ активных сил; 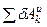 – сумма элементарных работ сил инерции.
– сумма элементарных работ сил инерции.
2. Изображаем на чертеже активные силы 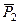 ,
, 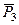 ,
, 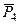 и пару сил с моментом
и пару сил с моментом 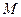 . Сообщим системе возможное перемещение
. Сообщим системе возможное перемещение 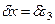 и составим выражение для суммы работ:
и составим выражение для суммы работ:
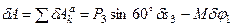 .
.
Выразим 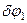 через
через 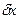 :
:
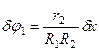 .
.
В результате получим
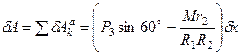 . (271)
. (271)
3. Задавшись направлением ускорения 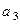 , изображаем на чертеже силы инерции
, изображаем на чертеже силы инерции 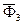 ,
, 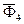 и пару сил инерции с моментом
и пару сил инерции с моментом 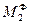 , величины которых равны:
, величины которых равны:
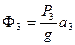 ,
, 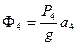 ,
,  . (272)
. (272)
Сообщая системе возможное перемещение 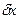 , получим:
, получим:
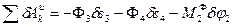 . (273)
. (273)
Выразим все ускорения, входящие в (272) через искомую величину 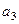
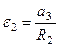 ,
, 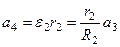 ,
,
а перемещения через 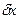 :
:
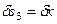 ,
, 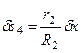 ,
,  .
.
В результате получим:
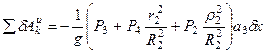 . (274)
. (274)
Подставив величины 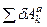 и
и 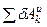 (формулы (271) и (274)) в уравнение (270), и сократив на
(формулы (271) и (274)) в уравнение (270), и сократив на 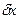 , найдем:
, найдем:
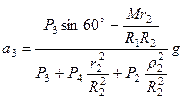 . (275)
. (275)
Вычисления дают 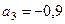 м/с2. Знак указывает, что ускорение груза 3 и ускорения других тел направлены противоположно показанным на рис. 60.
м/с2. Знак указывает, что ускорение груза 3 и ускорения других тел направлены противоположно показанным на рис. 60.
Ответ: 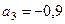 м/с2, ускорение груза 3 и ускорения других тел направлены противоположно показанным на рисунке.
м/с2, ускорение груза 3 и ускорения других тел направлены противоположно показанным на рисунке.
Пример 12.
Механическая система (рис. 60) состоит из обмотанных нитями блока 1 радиуса 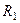 и ступенчатого шкива 2 (радиусы ступеней
и ступенчатого шкива 2 (радиусы ступеней 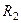 и
и  , радиус инерции относительно оси вращения
, радиус инерции относительно оси вращения 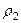 ), и из грузов 3 и 4, прикрепленных к этим нитям. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом
), и из грузов 3 и 4, прикрепленных к этим нитям. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом 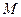 , приложенной к блоку 1.
, приложенной к блоку 1.
Дано: 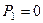 Н,
Н, 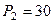 Н,
Н, 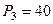 Н,
Н, 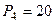 Н,
Н, 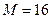
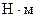 ,
, 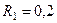 м,
м, 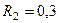 м,
м, 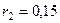 м;
м; 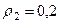 м.
м.
Определить: ускорение груза 3, пренебрегая трением.
Решение:
1. Система имеет одну степень свободы. Выберем в качестве обобщенной координаты перемещение 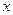 груза 3, полагая, что он движется вниз и отсчитывая
груза 3, полагая, что он движется вниз и отсчитывая 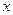 в сторону движения (рис. 60). Составим уравнение Лагранжа:
в сторону движения (рис. 60). Составим уравнение Лагранжа:
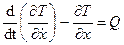 . (276)
. (276)
2. Определим кинетическую энергию всей системы, равную сумме кинетических энергий всех тел:
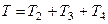 . (277)
. (277)
Грузы 3 и 4 движутся поступательно, поэтому шкив 2 вращается вокруг неподвижной оси, следовательно
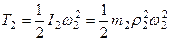 ,
, 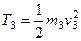 ,
, 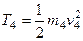 . (278)
. (278)
Скорости 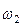 ,
, 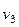 и
и 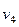 выразим через обобщенную скорость
выразим через обобщенную скорость 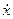 :
:
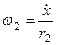 ,
, 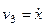 ,
, 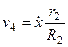 . (279)
. (279)
Подставляя значения величин (279) в равенства (278), а затем значения 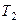 ,
, 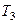 и
и 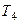 в соотношение (277), получим:
в соотношение (277), получим:
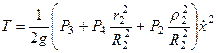 . (280)
. (280)
Так как кинетическая энергия зависит только от 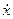 , производные левой части уравнения (276) примут вид:
, производные левой части уравнения (276) примут вид:
 ,
,
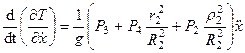 ,
, 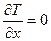 . (281)
. (281)
3. Найдем обобщенную силу 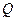 . Для этого составим уравнение работ активных сил на перемещении
. Для этого составим уравнение работ активных сил на перемещении 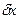 . Воспользуемся соотношением (271) примера 11:
. Воспользуемся соотношением (271) примера 11:
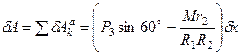 . (282)
. (282)
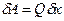 .
.
Коэффициент при 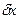 в (282) и будет обобщенной силой:
в (282) и будет обобщенной силой:
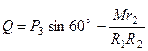 . (283)
. (283)
Подставляя (281) и (283) в уравнение (276), получим
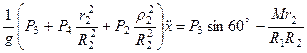 .
.
Отсюда находим
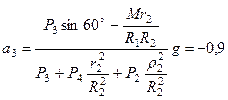 м/с2,
м/с2,
что совпадает с ответом примера 11.
Ответ: 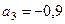 м/с2, что ускорение груза 3 и ускорения других тел направлены противоположно показанным на рисунке.
м/с2, что ускорение груза 3 и ускорения других тел направлены противоположно показанным на рисунке.
Контрольные Вопросы
1. Основные понятия статики.
2. Алгебраический и векторный момент силы относительно точки.
3. Момент силы относительно оси.
4. Пара сил и момент пары сил.
5. Аксиомы статики.
6. Простейшие теоремы статики.
7. Система сходящихся сил.
8. Эквивалентность пар сил.
9. Условия равновесия пар сил.
10. Приведение произвольной системы сил к простейшему виду.
11. Формы условия равновесия пространственной системы сил.
12. Условия равновесия пространственной системы параллельных сил.
13. Теорема Вариньона.
14. Формы условий равновесия плоской системы сил.
15. Распределенные силы.
16. Типы реакций связей.
17. Сила трения скольжения.
18. Трение качения.
19. Определения и формулы для вычисления центров тяжести
20. Методы определения центров тяжести
21. Центры тяжести простейших тел.
22. Кинематика точки: скорость и ускорение точки.
23. Векторный способ изучения движения точки.
24. Координатный способ изучения движения точки.
25. Естественный способ изучения движения точки.
26. Теорема о проекциях скоростей.
27. Поступательное движение твердого тела.
28. Вращение твердого тела вокруг неподвижной оси.
29. Плоское движение твердого тела.
30. Мгновенный центр скоростей.
31. Мгновенный центр ускорений.
32. Сложение скоростей (общий случай переносного движения).
33. Сложение ускорений (общий случай переносного движения).
34. Ускорение Кориолиса.
35. Аксиомы динамики.
36. Дифференциальные уравнения движения материальной точки.
37. Основные задачи динамики точки.
38. Дифференциальные уравнения относительного движения материальной точки.
39. Дифференциальные уравнения движения точки в неинерциальной системе отсчета.
40. Основное свойство внутренних сил.
41. Геометрия центра масс.
42. Моменты инерции относительно точки и оси.
43. Моменты инерции относительно осей координат
44. Теорема Штейнера.
45. Моменты инерции однородных простейших тел.
46. Количество движения точки и системы, элементарный и полный импульсы силы.
47. Теорема о движении центра масс системы.
48. Теорема об изменении количества движения точки.
49. Теорема об изменении количества движения системы.
50. Законы сохранения количества движения.
51. Кинетический момент точки и системы.
52. Кинетический момент относительно оси вращения при вращательном движении твердого тела.
53. Теорема об изменении кинетического момента точки.
54. Теорема об изменении кинетического момента системы.
55. Законы сохранения кинетических моментов.
56. Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.
57. Теорема об изменении кинетического момента системы в относительном движении по отношению к центру масс.
58. Дифференциальные уравнения плоского движ
Дата добавления: 2017-09-01; просмотров: 2067;











