Уравнение неразрывности (сплошности) потока

Представляет собой зависимость между скоростями в потоке жидкости, для которого соблюдается условие сплошности, или неразрывности течения, т.е. не образуется пустот, не заполненных жидкостью.

Уравнение выражает фундаментальный закон сохранения массы (расхода).

Дифференциальное уравнение неразрывности для неустановившегося течения имеет вид

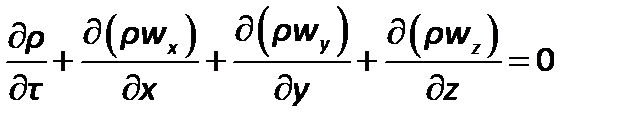
(2.35)

В установившемся потоке плотность не меняется во времени 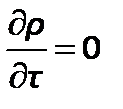, поэтому уравнение неразрывности выглядит так:

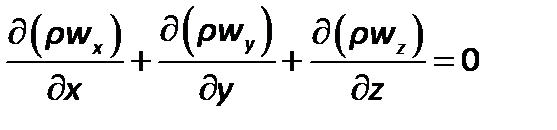
(2.36)

Для капельных жидкостей, которые практически несжимаемы, а также для газов в условиях изотермического потока, при скоростях меньших скорости звука, , следовательно, уравнение неразрывности примет вид:

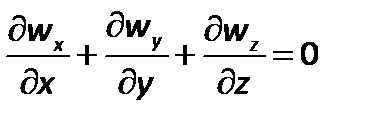
(2.37)

Для трубопровода постоянного сечения в результате интегрированиядифференциального уравнения неразрывности для установившегося однонаправленного движения жидкости (в направлении оси 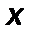) получается зависимость

.

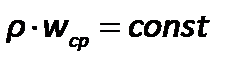Если же площадь сечения трубопровода переменна, тоинтегрирование по площади приводит к зависимости

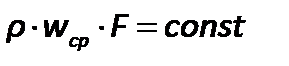
(2.38)

Для трех сечений трубопровода одного и того же потока жидкости (рис.2.6).

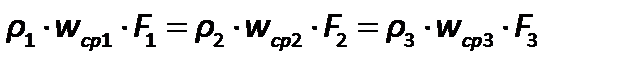
(2.39)

или для массового расхода жидкости в трубопроводе переменного сечения

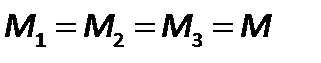
(2.40)

Согласно уравнению постоянства расхода, при установившемся течении жидкости, полностью заполняющей трубопровод, через каждое его поперечное сечение проходит в единицу времени одно и то же количество жидкости.

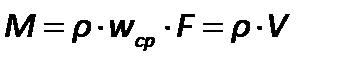
(2.41)

при

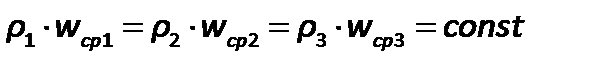
(2.42)

или для объемного расхода жидкости в трубопроводе переменного сечения

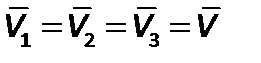
(2.43)

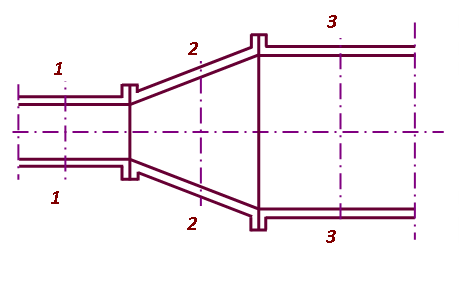
Рис. 2.6. К выводу уравнения постоянства расхода

Из уравнения (2.42) следует, что скорости капельной жидкости в различных поперечных сечениях трубопровода обратно пропорциональны площадям этих сечений.

В соответствии с уравнением (2.38), массовый расход жидкости через начальное сечение трубопровода равен ее расходу через конечное сечение трубопровода. Таким образом, уравнение неразрывности является частным случаем закона сохранения массы и выражает материальный баланс потока.