Статистический характер II начала термодинамики. Теорема Нернста. Недостижимость абсолютного нуля температуры.
II начало термодинамики, как физическая закономерность отличается от первого начала термодинамики. Закон сохранения энергии выполняется одинаково, как для макроскопических тел, так и для отдельных атомов и молекул. Опыты показывают, что II начало термодинамики применимо к системам, которые содержат большое количество молекул (частиц).
При применении II начала термодинамики к объектам, которые содержат малое число молекул (частиц) наблюдаются отклонения от этого закона.
Например, броуновское движение не подчиняется II началу термодинамики, оно противоречит II началу термодинамики. Броуновская частица получает энергию от молекул окружающей среды (жидкости), температура которой равна температуре броуновской частички. При этом нарушается II начало термодинамики: теплота переходит в работу без каких-либо изменений в окружающей среде.
Это объясняется тем, что II начало термодинамики – статистический закон. Явления, которые происходят в макроскопической системе, складывающейся из большого числа микрочастиц, носят статистический характер.
Статистический подход ко II началу термодинамики основан на применении для оценки того или иного состояния системы понятия вероятности.
Состояние системы, которое характеризуется ее термодинамическими параметрами, называется макроскопическим состоянием.
Состояние системы, которое характеризуется состоянием каждой ее молекулы (частицы), называется микроскопическим состоянием.
Каждое микроскопическое состояние системы характеризуется определенной вероятностью. Молекулы газа двигаются хаотично, поэтому существует много возможных микроскопических состояний, соответствующих определенному макроскопическому состоянию системы. Если считать, что все микроскопические состояния равновероятны, то можно найти вероятность данного макроскопического состояния.
Однако такой способ оценки вероятности того или иного макроскопического состояния достаточно сложный.
Поэтому в статистической физике используют термодинамическую вероятность, или статистический вес макроскопического состояния.
Термодинамическая вероятность W макроскопического состояния – это число способов (число микроскопических состояний), которыми может быть осуществлено данное макроскопическое состояние.
В отличие от математической вероятности, которая не может быть больше единицы, термодинамическая вероятность всегда много больше, либо равна единице.
Рассмотрим газ, который состоит из четырех молекул с номерами 1,2,3,4. Пусть этот газ находится в половине A сосуда с перегородкой. Другая половина сосуда B – пустая (рис.1).
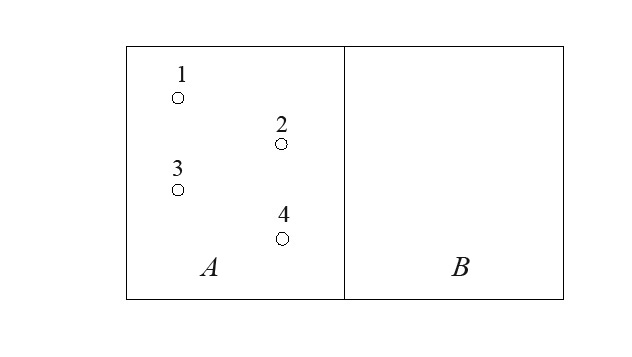
Рис.1. Распределение молекул между двумя половинами сосуда
Если удалить перегородку, то молекулы, двигаясь хаотично, могут оказаться в разные моменты времени как в половине A, так и в половине B данного сосуда. Поэтому в разные моменты времени будут возникать различные распределения молекул между половинами A и B сосуда: поровну, три слева одна справа, и т.д.
Подсчитаем число способов распределения молекул между двумя половинами сосуда (табл.1)
Таблица 1:
| Состояние | Способ реализации состояния | Число способов реализации данного состояния (термодинамическая вероятность W) | ||
| Число молекул, A | Число молекул, B | №,№ молекул A | №,№ молекул B | |
| - | 1,2,3,4 | |||
| 2,3,4 | ||||
| 1,3,4 | ||||
| 1,2,4 | ||||
| 1,2,3 | ||||
| 1,2 | 3,4 | |||
| 1,3 | 2,4 | |||
| 1,4 | 2,3 | |||
| 2,3 | 1,4 | |||
| 2,4 | 1,3 | |||
| 3,4 | 1,2 | |||
| 1,2,3 | ||||
| 1,2,4 | ||||
| 1,3,4 | ||||
| 2,3,4 | ||||
| 1,2,3,4 | - | |||
| Всего способов: | 24 = 16 |
Каждая молекула с равной вероятностью может оказаться, как в половине A, так и в половине B сосуда. Следовательно, каждое из 16 распределений молекул между половинками сосуда может осуществляться одинаково часто.
Поэтому число способов реализации данного состояния определяет вероятность данного состояния. Как видно из таблицы наибольшее число способов распределения осуществляет такое состояние, при котором и слева и справа будет по две молекулы, т.е. равномерное распределение молекул между двумя половинами сосуда: число способов размещения – 6, математическая вероятность 1/6.
Может случиться, что все 4 молекулы опять окажутся в половине A сосуда. Это значит, что газ, который расширился, самопроизвольно сжался. Расширение газа в пустоту оказывается обратимым процессом, что противоречит II началу термодинамики. Однако только одно распределение молекул из 16 создает такое состояние, при котором все молекулы соберутся в половине A сосуда.
Математическая вероятность такого события 1/16 – мала по сравнению с вероятностями других размещений, но не очень, при небольшом общем числе молекул.
Как видно из таблицы общее число способов распределения n молекул жду двумя половинами сосуда – 2n. В реальных системах число молекул очень велико. В 1см3 воздуха при нормальных условиях, находится ~ 1020 молекул. Общее число способов распределения молекул между двумя половинами сосуда (V = 1см3) равно:
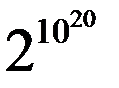
И, только один из этих способов будет соответствовать тому, что все молекулы соберутся в половине A этого сосуда.
Такое событие возможно, однако его математическая вероятность будет равна:
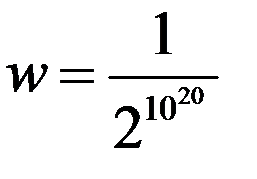
Эта вероятность настолько мала, что практически осуществиться не может. И наоборот, число способов, которыми осуществляется равномерное распределение молекул в объеме сосуда значительно больше по сравнению с любым другим распределением.
Состояние равномерного распределения молекул по объему сосуда наиболее вероятное и является равновесным.
Отсюда следует, что процесс самопроизвольного сжатия газа очень маловероятный. Иначе говоря, процесс расширения сжатого газа на весь сосуд необратимый, потому что обратный процесс самопроизвольного сжатия газа очень маловероятный.
Обобщая вышеизложенное можно сделать вывод: всякий необратимый процесс – это такой процесс, обратный которому очень маловероятный.
Статистический характер II начала термодинамики хорошо выявляется в формулировке Больцмана:
Природа стремится от менее вероятных состояний к более вероятным.
Из всех видов движения наиболее вероятным является хаотическое (тепловое) движение молекул. Поэтому любое упорядоченное движение молекул всегда стремится перейти в неупорядоченное.
При выполнении работы происходит переход макроскопического, упорядоченного движения тела, под действием внешних сил в неупорядоченное, хаотическое движение молекул (нагревание тел из-за сил трения). Этот переход более вероятен. Получение работы за счет теплоты означает переход хаотичного движения молекул в упорядоченное движение макроскопического тела. Такой переход менее вероятен.
II начало термодинамики показывает необратимость перехода работы в теплоту. Это значит, что обратный переход теплоты в работу соответствует переходу от более вероятного состояния к менее вероятному.
Если изолированная система находится в состоянии с максимальной энтропией, которая соответствует состоянию с максимальной вероятностью, то в ней не могут самопроизвольно протекать какие-либо процессы. Максимальная энтропия системы соответствует состоянию равновесия. Когда такое состояние достигается, то любые изменения в системе без внешних воздействий прекращаются. Любой самопроизвольный процесс в таком состоянии приводил бы к уменьшению энтропии, а, следовательно, к уменьшению вероятности такого состояния, что невозможно.
Поэтому состояние с максимальной энтропией – наиболее устойчивое состояние системы.
Энтропия может быть связана с величиной термодинамической вероятности, поскольку и та и другая величина имеет максимальное значение в состоянии равновесия и переход всякой системы в состояние равновесия сопровождается как возрастанием энтропии, так и термодинамической вероятности.
Статистическая причина увеличения энтропии при протекании необратимых процессов заключается в том, что при этом увеличивается термодинамическая вероятность состояния системы. Поэтому энтропия S должна быть некоторой функцией термодинамической вероятности W. Больцман показал, что:
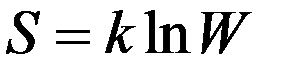 (1)
(1)
где k – постоянная Больцмана, W – термодинамическая вероятность состояния, для которого подсчитывается энтропия.
Как было показано выше, состояние с большим беспорядком характеризуется большей термодинамической вероятностью, чем более упорядоченное состояние. Следовательно, чем больший беспорядок в системе, тем больше энтропия системы. Любой естественный процесс всегда протекает так, что система переходит в состояние с большим беспорядком: температуры разных тел выравниваются, газы перемешиваются и т.д. Поэтому энтропию можно считать мерой беспорядка системы.
С беспорядком связана и необратимость тепловых процессов: тепловые процессы всегда протекают так, что беспорядок в системе увеличивается. С этим связан и тот факт, что любой вид энергии, в конце концов, переходит в теплоту, потому что тепловая энергия это энергия беспорядочного, хаотичного движения молекул, а все другие виды энергии связаны с более упорядоченным движением.
Связь между энтропией и вероятностью позволяет несколько иначе трактовать II начало термодинамики. II начало термодинамики утрачивает свою категоричность: если система находится в каком-либо состоянии с данным значением энтропии, то с очень большой вероятностью она перейдет в состояние с большей энтропией.
Это означает, что более вероятным изменением энтропии является ее рост. Однако, принципиально возможны и процессы, сопровождающиеся и уменьшением энтропии. Например, флуктуации давления газа, его плотности это такие изменения состояния, которые сопровождаются уменьшением энтропии и, следовательно, вероятности данного состояния. Но эти малые отклонения от равновесного состояния не противоречат II началу термодинамики, они являются следствием именно вероятностного характера энтропии.
Уравнение:
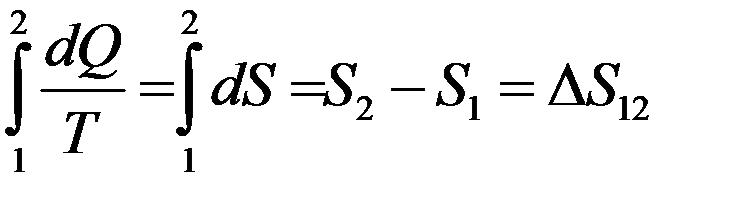 (2)
(2)
позволяет определить не абсолютное значение энтропии, а только разность ее значений в двух состояниях. Определить значение энтропии в любом состоянии дает возможность теорема Нернста:
При абсолютном нуле температуры любые изменения состояния происходят без изменения энтропии.
Либо:
При стремлении температуры к абсолютному нулю энтропия любого тела (системы) также стремится к нулю.
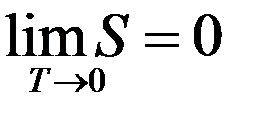 (3)
(3)
Согласно этой теореме энтропия любого тела (системы) равна нулю, если T = 0, т.е.:
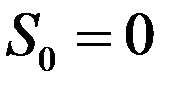
Следовательно, энтропия тела (системы) в состоянии с температурой T может быть рассчитана следующим образом:
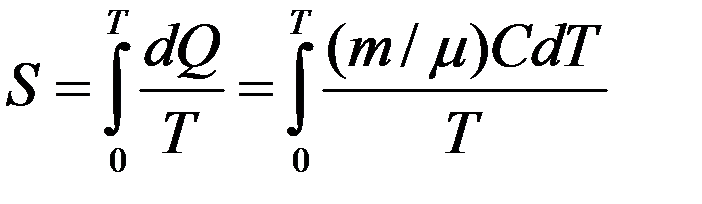 (4)
(4)
Для определения S из (6) необходимо знать молярную теплоемкость C, т.к. ее значение зависит от вида процесса и температуры.
Из теоремы Нернста следует, что абсолютный нуль температуры принципиально не достижим, т.к. при стремлении температуры к нулю, согласно (4) изменение энтропии должно стремиться к бесконечности, что противоречит теореме Нернста. Теорема Нернста применима только для систем, находящихся в состоянии термодинамического равновесия и не справедлива для неравновесных систем.
Сформулируем основные свойства энтропии:
1. Энтропия является функцией состояния системы;
2. Для подсчета изменения энтропии при переходе системы из состояния 1 в состояние 2 необходимо подсчитать значение интеграла (4) для любого обратимого процесса, приводящего систему из состояния 1 в состояние 2;
3. Энтропия замкнутой системы остается постоянной, если в системе протекают обратимые процессы и возрастает, если в системе протекают необратимые процессы;
4. Максимальное значение энтропии соответствует состоянию термодинамического равновесия системы;
5. Энтропия непосредственно связана с термодинамической вероятностью состояния системы;
6. Возрастание энтропии при необратимых процессах означает, что энергия, которой обладает система, становится менее доступной для преобразования в механическую работу;
7. В состоянии равновесия, когда энтропия максимальна, энергия системы вообще не может быть преобразована в работу.
Дата добавления: 2017-09-01; просмотров: 2244;











