Теоремы Карно. Реальные циклы. Приведенная теплота. Энтропия. Закон возрастания энтропии в изолированной системе.
Цикл Карно проводится таким образом, что тела с разной температурой не соприкасаются. Следовательно, из этого цикла исключены необратимые процессы теплопроводности. Отсюда следует, что цикл Карно обеспечивает наилучшие условия для преобразования теплоты в работу. Поэтому получить более высокий КПД, чем в цикле Карно практически невозможно.
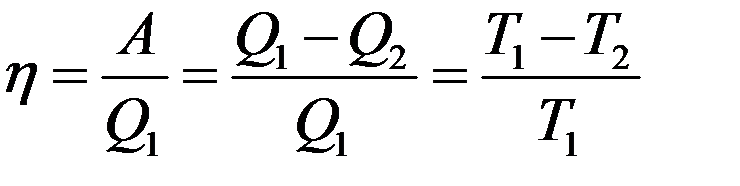 (1)
(1)
В этом утверждении и состоит суть теорем Карно:
1. КПД тепловой машины, работающей при данных значениях температур нагревателя и холодильника, не может быть больше, чем КПД машины, работающей по обратимому циклу Карно при тех же значениях температур нагревателя и холодильника.
2. КПД цикла Карно не зависит от рода рабочего тела и определяется только температурами нагревателя и холодильника.
Докажем эти теоремы. Рассмотрим работу двух тепловых машин с единым нагревателем и с единым холодильником (рис.1).
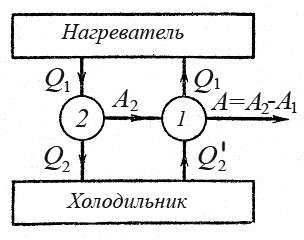
Рис.1. Работа сопряженных тепловой и холодильной машин
Пусть машина 1 работает по обратимому циклу Карно, а машина 2 отличается от машины 1 необратимостью процессов в ней. Предположим, что η2 > η1. Соединим машины так, чтобы одна из них приводила в движение другую. Пусть машина 2 работает по прямому циклу. Она получает от нагревателя теплоту Q1, выполняет работу A2 и отдает холодильнику теплоту:
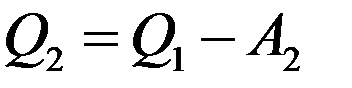 (2)
(2)
При этом машина 2 приводит в движение машину 1, которая работает по обратному циклу Карно, т.е. как холодильная машина. Машина 1 передает теплоту от холодильника нагревателю за счет работы выполненной над ней машиной 2. Пусть машина 1 передает нагревателю за один цикл теплоту Q1, такую же, как машина 2 получает от нагревателя за один цикл. Для этого над машиной 1 необходимо выполнить работу A1. Тогда теплота, отнятая машиной 1 от холодильника:
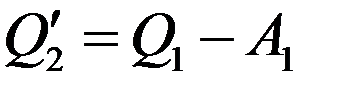 (3)
(3)
За один цикл работы двух машин получим:
1. состояние нагревателя не изменилось, так как машина 1 передала ему столько же тепла, сколько получила машина 2;
2. рабочее тело в каждой из машин вернулось в исходное состояние, совершив круговой процесс, т.е. состояние рабочих тел так же не изменилось;
3. холодильник получил от машины 2 теплоту Q2, а машина 1 отняла у него теплоту Q'2.
Поскольку η2 > η1, то согласно (1) A2 > A1 и из (2) и (3) следует:
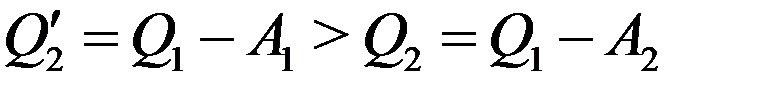 (4)
(4)
Согласно (4) единственным результатом цикла явилось извлечение из холодильника теплоты Q'2 - Q2 и превращение его в работу:
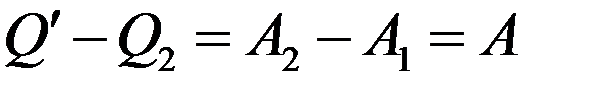
Однако это противоречит II началу термодинамики (принцип Томсона). Следовательно, η2 не может быть больше чем КПД η1 обратимой машины Карно.
Вторая теорема Карно. Рассмотрим еще раз соединенные вместе тепловые машины 1 и 2 с общим для них нагревателем и холодильником, но с разными рабочими телами (рис.1). Пусть машина 2 совершает прямой цикл Карно, а машина 1 обратный и, например, η2 > η1. Совершая прямой цикл, машина 2 получает от нагревателя теплоту Q1, отдает холодильнику теплоту Q2 и совершает работу A2 = Q1 - Q2.
Машина 1, совершая обратный цикл, забирает у холодильника теплоту Q'2 и отдает нагревателю теплоту Q1, такую же, как получает от нагревателя машина 2. Для этого над машиной 1 надо выполнить работу A1 = Q1 - Q'2. Если η2 > η1, то A2 > A1, следовательно, Q1 - Q2 > Q1 - Q'2, или Q'2 > Q2. Это значит, что разность Q'2 - Q2 преобразовывается в работу.
В результате цикла состояние нагревателя и рабочего тела не изменилось. Следовательно, единственный результат цикла - извлечение из холодильника теплоты Q'2 - Q2 и преобразование его в работу, что противоречит II началу термодинамики. Поэтому η2 не может быть больше η1.
Изменяя порядок работы машин, т.е. предположив, что машина 1 совершает прямой цикл, а машина 2 – обратный и аналогично рассуждая, получим, что η1 не может быть больше η2. Остается только одна возможность: η1 = η2.
Так как в одной из машин рабочим телом может быть идеальный газ, а для этого случая:
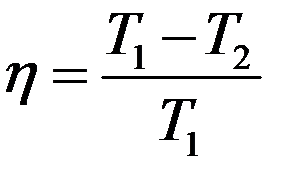
где T1 – температура нагревателя, а T2 – температура холодильника, то отсюда следует, что для любой обратимой машины Карно КПД будет таким же.
Для необратимого цикла:
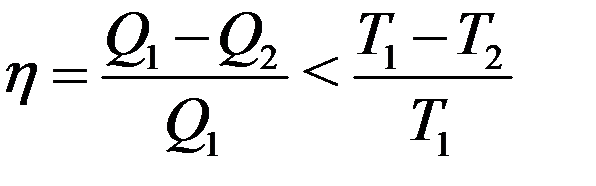 (5)
(5)
В технике широко используются тепловые машины, среди них двигатели внутреннего сгорания, использующие энергию сгорания топлива для выполнения полезной работы. В современных двигателях внутреннего сгорания наиболее распространены следующие циклы:
1. Цикл с подводом теплоты при постоянном объеме – цикл Отто;
2. Цикл с подводом теплоты при постоянном давлении – цикл Дизеля.
Рассмотрим цикл Отто. По такому циклу работают карбюраторные двигатели. В них используются высококачественные виды топлива с низкой температурой воспламенения – бензины (рис.2 (1)).
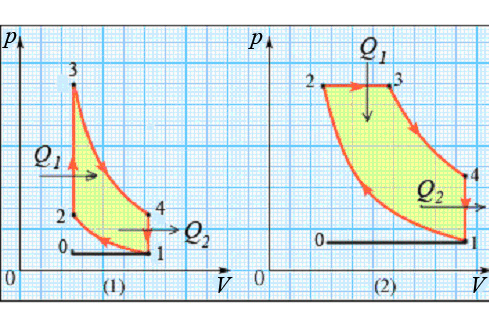
Рис.2. Циклы карбюраторного двигателя внутреннего сгорания (1) и дизельного двигателя (2)
Горючая смесь, подготовленная карбюратором, засасывается в цилиндр 0→1. Затем смесь адиабатно сжимается 1→2. В состоянии 2 смесь поджигается электрической искрой. Процесс сгорания происходит быстро и поршень практически не успевает прийти в движение, поэтому процесс сгорания топлива 2→3 можно считать изохорическим. При этом процессе рабочее тело получает количество теплоты Q1, выделившееся при сгорании топлива (V = const, A23 = 0):
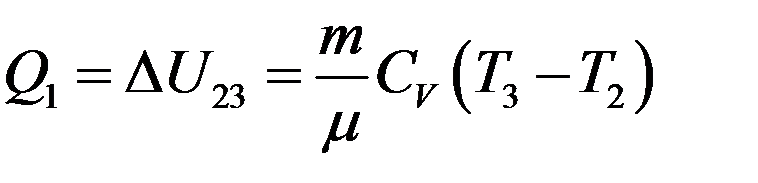 (6)
(6)
После этого продукты сгорания расширяются адиабатно 3→4 – рабочий ход поршня. В конце рабочего хода (точка 4) открывается выпускной клапан, и давление изохорически уменьшается до первоначального 4→1. При этом холодильнику (атмосфере) отдается теплота Q2 (V = const, A41 = 0):
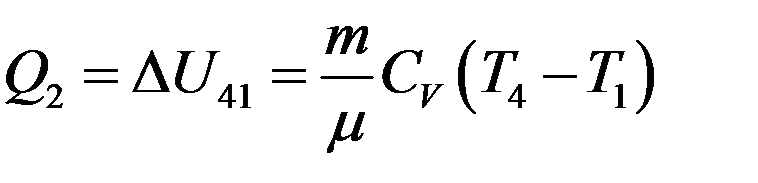 (7)
(7)
Затем продукты сгорания выталкиваются в атмосферу 1→0, и начинается новый цикл.
Определим КПД цикла Отто:
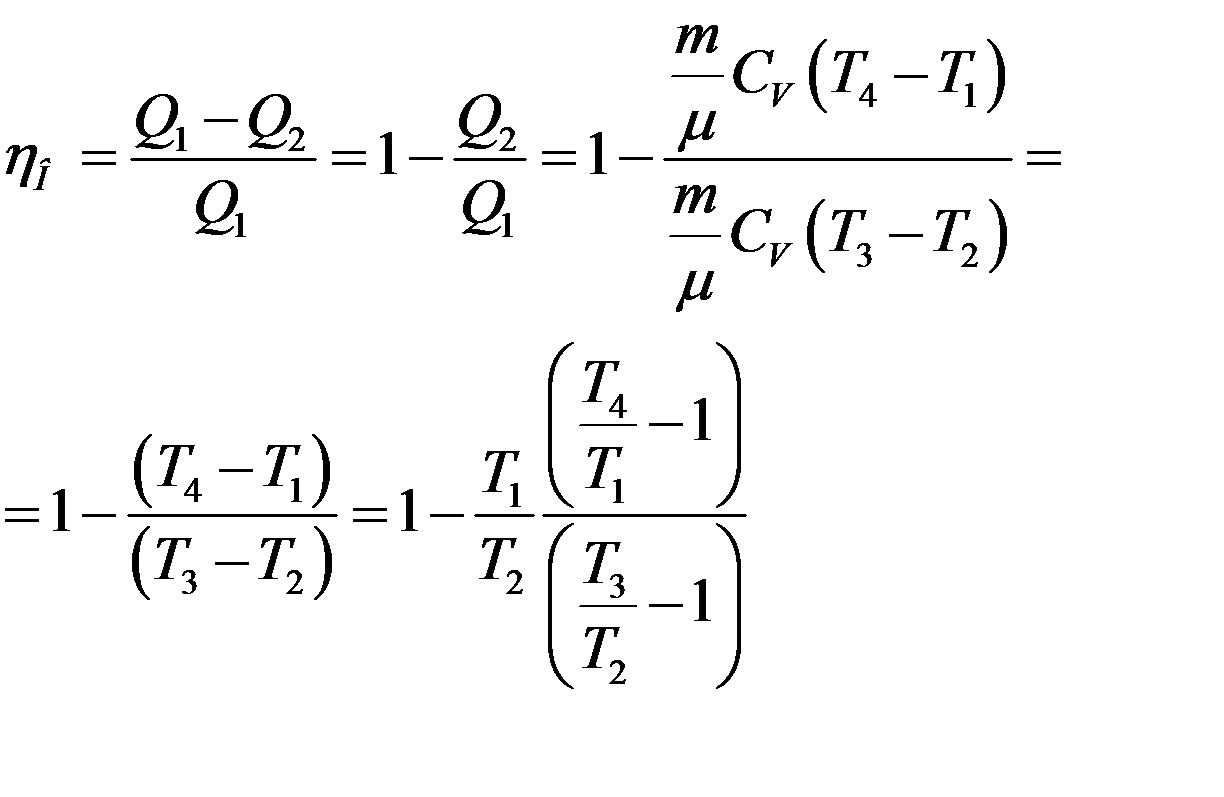 (8)
(8)
Запишем уравнения Пуассона для адиабат 1→2 и 3→4:
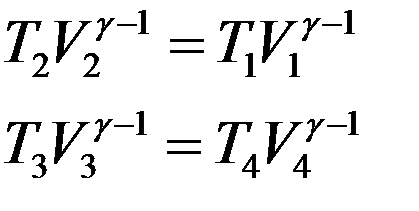 (9)
(9)
Разделим в (9) первое уравнение на второе:
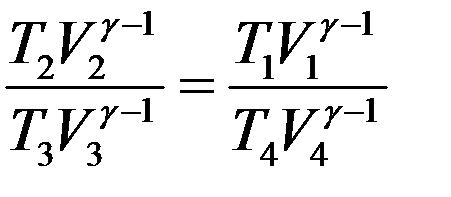
Учтем, что V2 = V3 и V1 = V4, тогда из последнего уравнения получим:
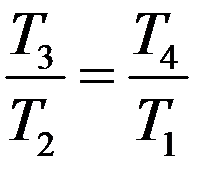 (10)
(10)
С учетом (10) из (8) получим:
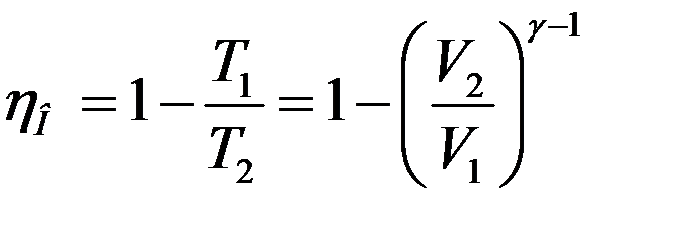 (11)
(11)
Минимальная температура цикла T1 максимальная - T3 и T2 < T3 поэтому:
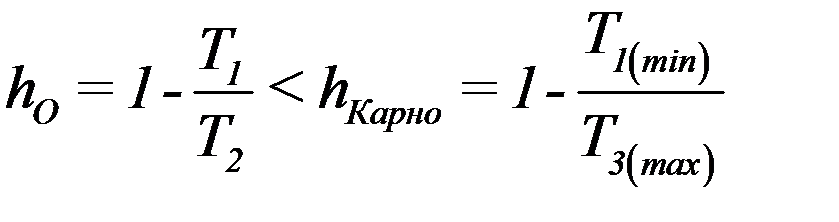
Как видно из (11) КПД цикла Отто возрастает при увеличении степени сжатия V1/V2. В современных двигателях степень сжатия достигает 10 – 12. При более высоких степенях сжатия температура смеси может стать большей, чем температура ее воспламенения. КПД лучших бензиновых двигателей достигает (25 – 30) %.
Рассмотрим цикл Дизеля (рис.2 (2)). В дизельных двигателях в цилиндр засасывается чистый воздух 0→1, затем он адиабатно сжимается 1→2 (степень сжатия ~30). При сжатии температура воздуха повышается до 900 – 1000 оС и становится выше температуры воспламенения топлива (солярка). Топливо впрыскивается в цилиндр форсункой (точка 2) и сгорает относительно медленно при постоянном давлении 2→3, при этом поршень двигается. В результате сгорания топлива рабочее тело получает теплоту Q1:
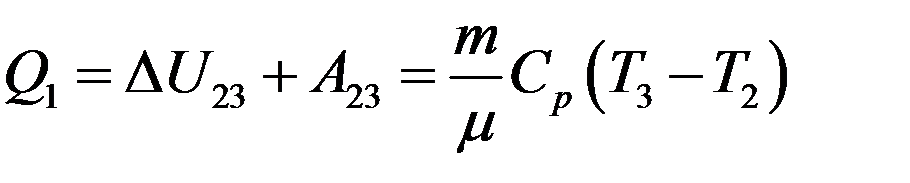 (12)
(12)
После этого продукты сгорания расширяются адиабатно 3→4. В точке 4 открывается выпускной клапан, продукты сгорания изохорно охлаждаются 4→1 и отдают холодильнику (атмосфере) теплоту Q2 (V = const, A41 = 0):
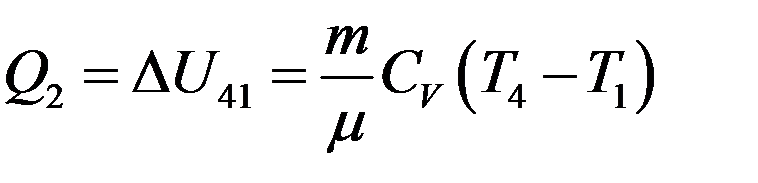 (13)
(13)
Затем продукты сгорания выталкиваются в атмосферу 1→0, и начинается новый цикл.
Определим КПД цикла Дизеля:
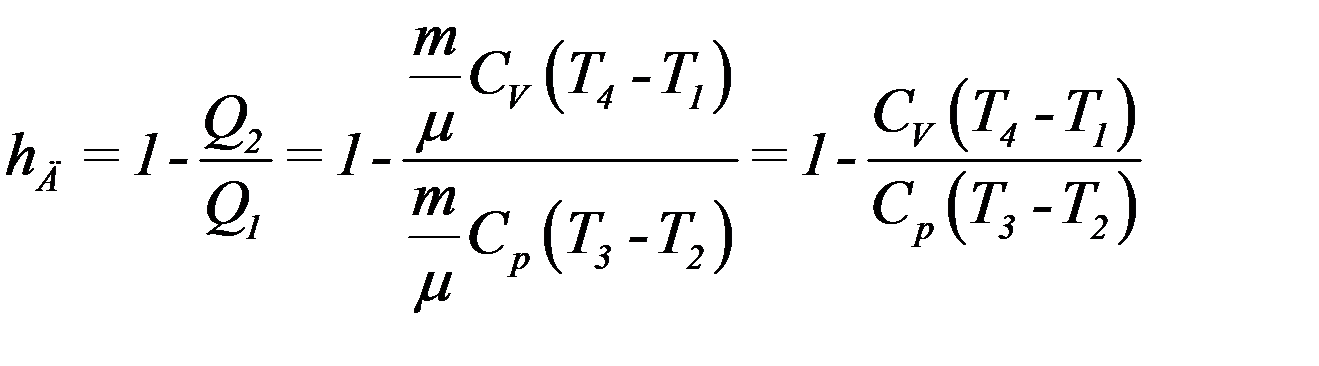
Учтем, что CV/Cp = 1/γ, тогда:
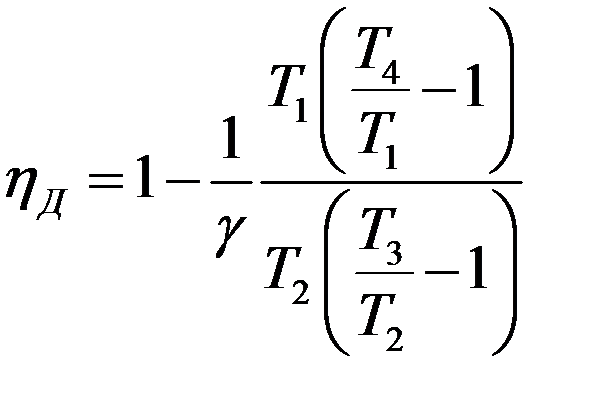
Умножим и разделим второе слагаемое в последнем уравнении на T3:
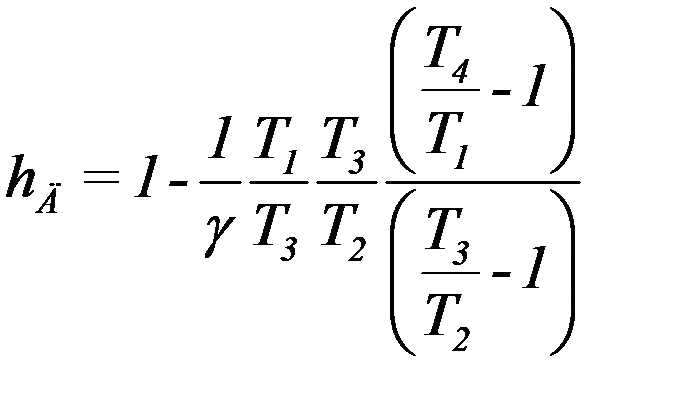 (14)
(14)
Запишем уравнение Пуассона для адиабат 1→2 и 3→4:
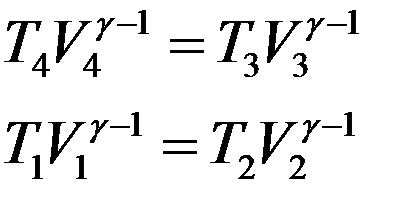
Разделим первое уравнение на второе с учетом того, что V4 = V1:
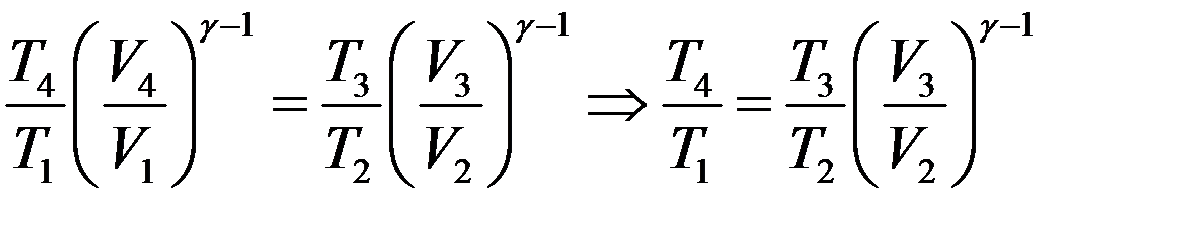 (15)
(15)
Для изобарического процесса 2→3:
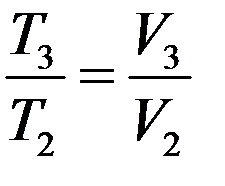
С учетом этого из (15) получим:
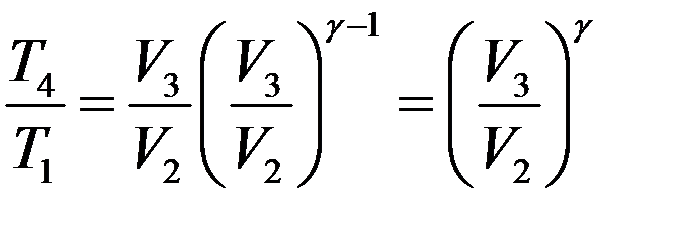 (16)
(16)
С учетом (16) из (14) получим:
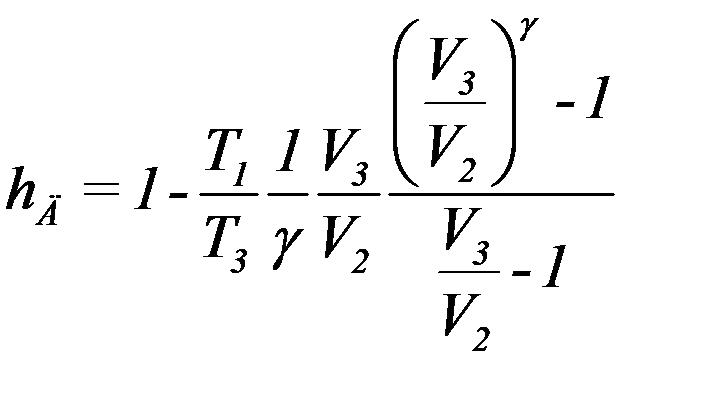 (17)
(17)
Обозначим в (17):
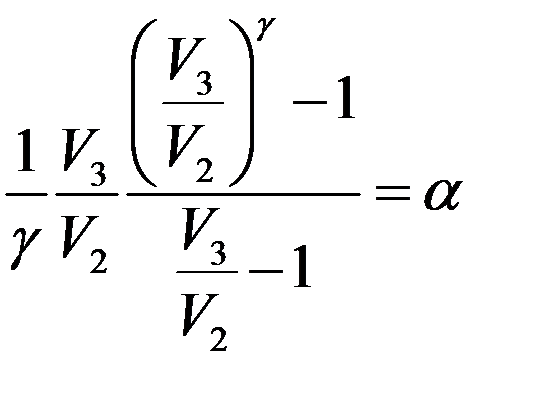
Очевидно, что α > 1, потому что V3 > V2 и γ > 1. С учетом этого:
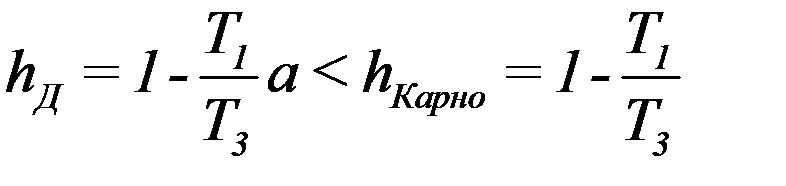
T1 – минимальная температура цикла, T3 – максимальная температура цикла. КПД цикла Дизеля достигает ~ 40%.
Согласно теореме Карно КПД всех обратимых машин не зависит от рода рабочего тела и определяется только температурой нагревателя T1 и холодильника T2.
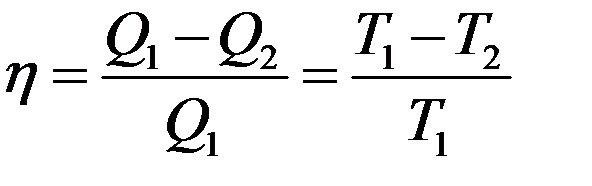 (18)
(18)
Преобразуем (18):
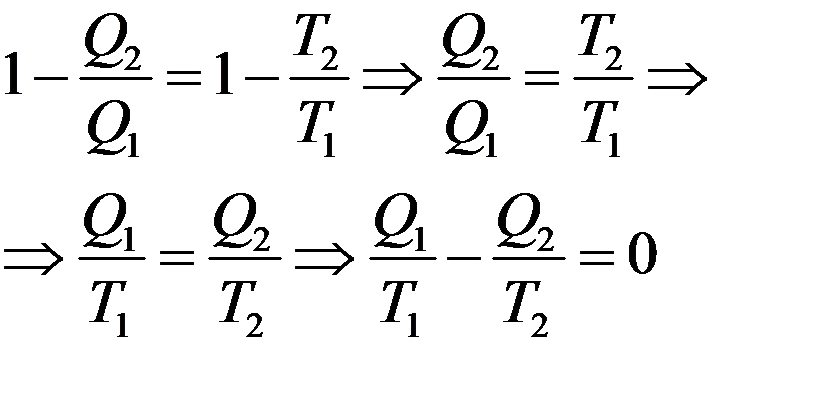 (19)
(19)
Если рассматривать работу тепловой машины с точки зрения изменений, которые происходят в рабочем теле, то Q1 – теплота, полученная рабочим телом, Q2 – теплота отданная им. Очевидно, этим величинам необходимо приписать противоположные знаки. Будем считать Q1 положительным, тогда Q2 – отрицательное. С учетом этого перепишем (19) в виде:
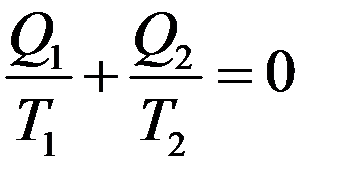 (20)
(20)
Отношение количества теплоты к температуре, при которой оно было получено или отдано называется приведенной теплотой.
Из (20) следует, что для обратимого цикла Карно алгебраическая сумма приведенных теплот равна нулю. Этот вывод справедлив для любого обратимого цикла.
Рассмотрим некоторый обратимый цикл 1a2b1 (рис.3):
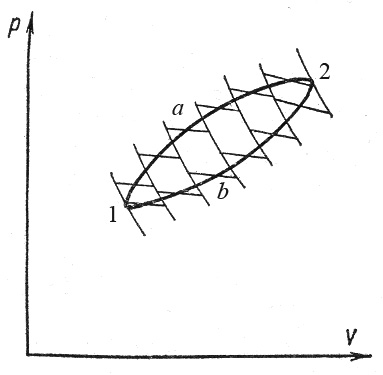
Рис. 3. К выводу неравенства Клаузиуса
Проведем ряд адиабат на бесконечно малом расстоянии одна от другой. Очевидно, что любой обратимый цикл можно разбить на ряд обратимых элементарных циклов, каждый из которых складывается из двух адиабат и двух элементарных отрезков, которые можно считать изотермами. Следовательно, в результате такого разбиения получится ряд элементарных, обратимых циклов Карно, для каждого из которых выполняется уравнение (20). Записав такие уравнения для каждого цикла, и просуммировав их, получим:
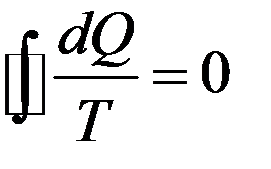 (21)
(21)
Представим этот интеграл для произвольного обратимого цикла 1a2b1 в виде суммы двух интегралов:
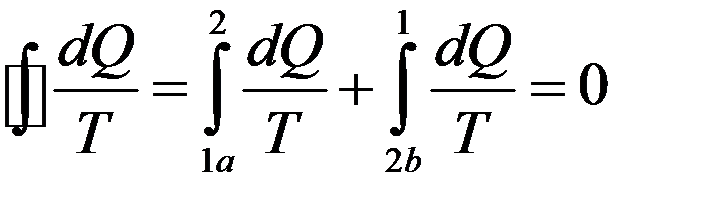 (22)
(22)
Очевидно, что если процесс обратимый, то:
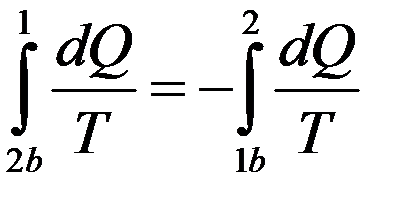 (23)
(23)
Это следует из того, что если при переходе 2b1 система, например, отдавала тепло, то при обратном переходе 1b2 она должна получать такое же количество теплоты (т.к. процесс перехода обратимый) и эти теплоты имеют разные знаки. С учетом (23) из (22) получим:
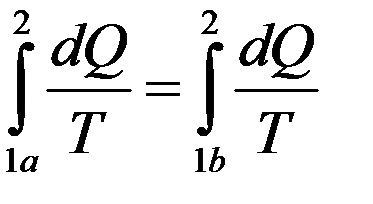 (24)
(24)
Из (24) видно, что интеграл, который выражает сумму приведенных теплот, не зависит от пути перехода между состояниями 1 и 2, а зависит только от начального и конечного состояния системы.
Независимость интеграла (24) от пути перехода означает, что этот интеграл выражает изменение некоторой функции параметров состояния системы. Эту функцию Клаузиус назвал энтропией – S (в переводе с греческого – превращать, преобразовывать).
Изменение энтропии системы, которая получила бесконечно малое количество теплоты δQ очевидно равно:
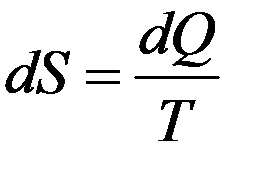 (25)
(25)
где dS – полный дифференциал функции параметров состояния. δQ – элементарное, бесконечно малое количество теплоты. Количество теплоты – функция процесса, следовательно, величина 1/T является интегрирующим множителем.
При обратимом процессе 1→2:
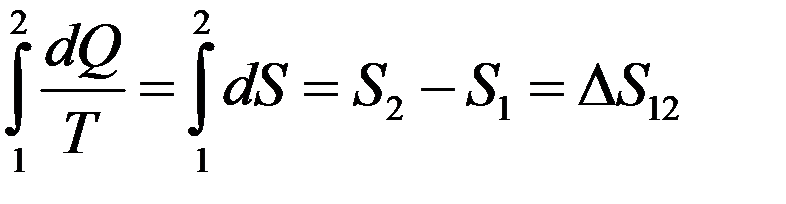 (26)
(26)
Формула (26) позволяет определить не абсолютное значение энтропии, а ее изменение при переходе системы из одного состояния в другое. Принято считать, что энтропия равна нулю при абсолютном нуле температур.
Пусть система выполняет круговой процесс по циклу Карно, получая теплоту от нагревателя и выполняя работу. При этом:
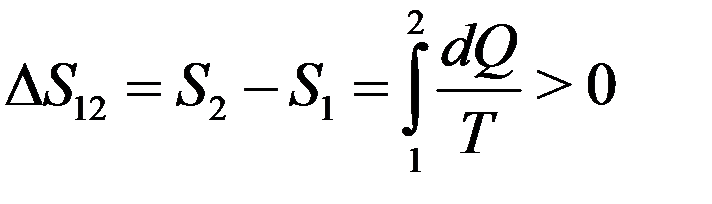 (27)
(27)
Полученная теплота считается положительной, поэтому энтропия системы возрастает. КПД цикла равен:
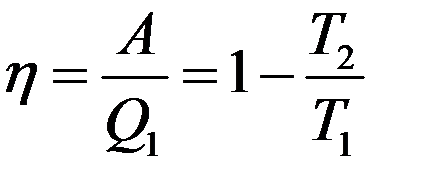 (28)
(28)
Если нагреватель будет иметь температуру меньшую, чем T1, то согласно (28) и (27) КПД цикла будет уменьшаться, а изменение энтропии системы будет возрастать. Если T1 увеличивать, то КПД процесса увеличивается, а изменение энтропии уменьшается.
Таким образом, возрастанию энтропии соответствует уменьшение КПД. Это значит, что уменьшается ценность нагревателя как источника энергии, которая преобразуется в работу. Рост энтропии приводит к обесцениванию тепловой энергии, к сокращению возможности получить за счет ее работу.
Пусть часть цикла, например 1a2 необратимая. КПД необратимой тепловой машины всегда меньше, чем обратимой (теорема Карно):
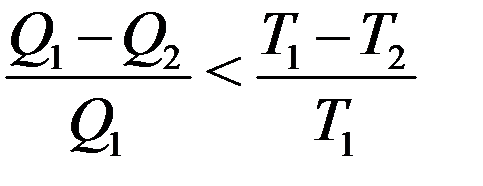
Преобразуем это неравенство с учетом того, что Q2 величина отрицательная:
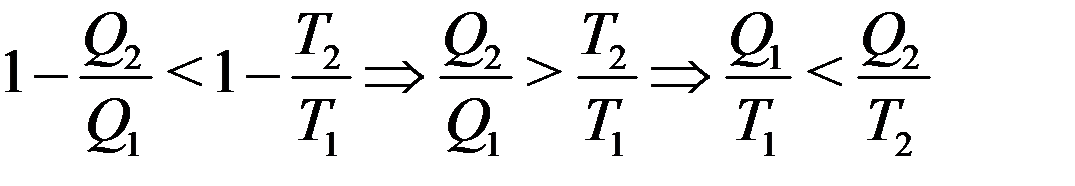
С учетом того, что Q2 < 0 из последнего уравнения получим:
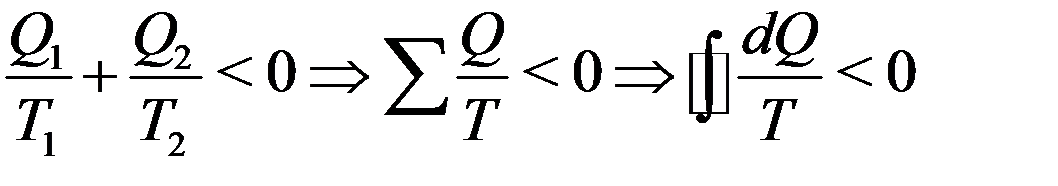 (29)
(29)
Из (29) следует, что для любого необратимого цикла сумма приведенных теплот меньше нуля. Формула (29) называется неравенством Клаузиуса. Интеграл (29) можно представить в виде:
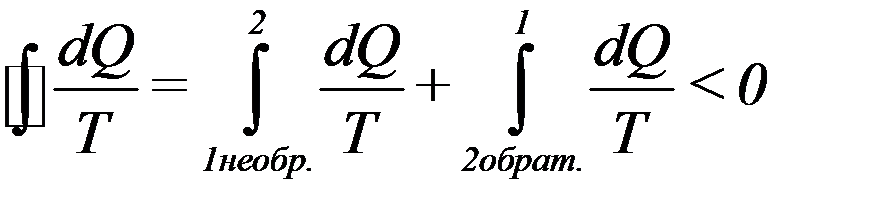
Или:
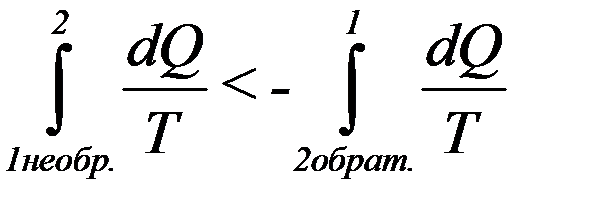 (30)
(30)
Учтем, что:
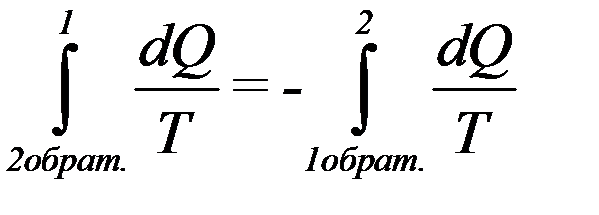 (31)
(31)
С учетом (31) из (30) получим:
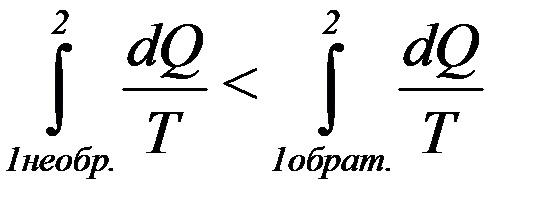 (32)
(32)
Согласно (26):
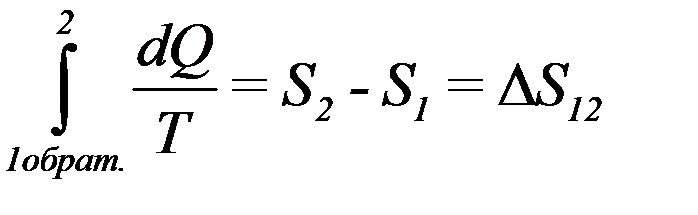 (33)
(33)
С учетом (33) перепишем (32) в виде:
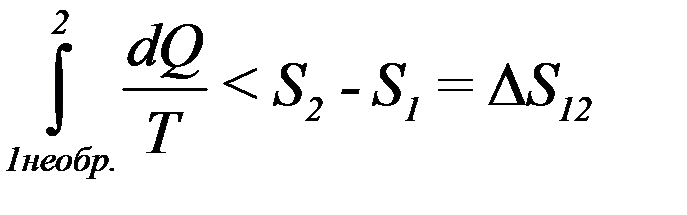 (34)
(34)
Из (34) следует, что при необратимом процессе интеграл от δQ/T всегда меньше изменения энтропии в этом процессе. Объединяя (34) и (26) получим:
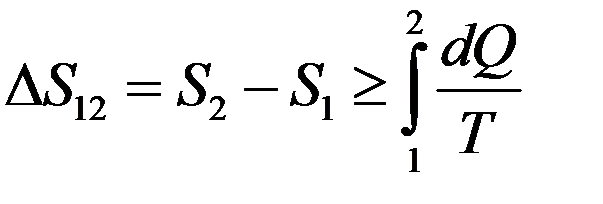 (35)
(35)
Если система изолирована и нет теплообмена с окружающей средой, то δQ = 0 и:
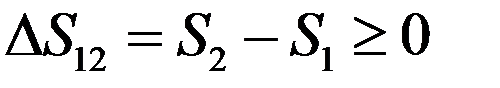
Из последнего уравнения следует, что энтропия изолированной системы может только возрастать, если в системе протекают необратимые процессы, или оставаться постоянной, если в системе протекают обратимые процессы. Энтропия изолированной системы уменьшаться не может. Это утверждение является одной из формулировок II начала термодинамики.
В любой изолированной системе, любой необратимый процесс протекает так, что количество энергии способной к преобразованию в работу, уменьшается, стремясь к нулю при равновесии, когда энтропия системы достигает максимального значения («тепловая смерть» вселенной).
В неизолированной системе энтропия может и уменьшаться (за счет работы внешних сил), но при этом в окружающей среде произойдут такие изменения, что суммарная энтропия системы и среды увеличится.
Лекция 15
Дата добавления: 2017-09-01; просмотров: 2862;











