Обратная задача теории погрешностей

На практике очень часто необходимо уметь решать обратную задачу: каковы должны быть абсолютные погрешности аргументов функции, чтобы абсолютная погрешность функции не превышала заданной величины.

Пусть величина предельной абсолютной погрешности Δ_u задана.

Тогда

Δ_u = .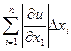

Предполагая, что все слагаемые равны между собой, будем иметь:

.

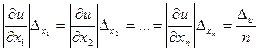Отсюда

Δ .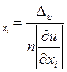

В случае, когда предельная абсолютная погрешность всех аргументов x_i одна и та же, то

;

.

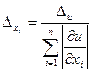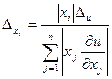Пример 1.20.

Радиус основания цилиндра R ≈ 2 м; высота цилиндра H ≈ 3 м. С какими абсолютными погрешностями нужно определить R и H, чтобы объем цилиндра V можно было вычислить с точностью до 0,1 м³?

Решение.

Объем вычисляется по формуле V = πR²H и Δ_V = 0.1 м³. Подставляя все исходные данные, приближенно получим:

;

;

.

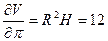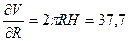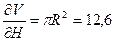Отсюда, т. к. n = 3, то, воспользовавшись формулой для вычисления погрешности функции, зависящей от трех переменных

,

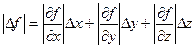будем иметь:

;

;

.

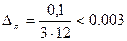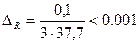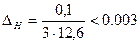Таблица 1.2. Погрешности значений элементарных функций

Функция Абсолютная погрешность Относительная погрешность

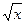
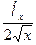
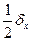
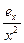
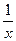
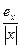
sin(x)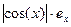

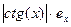
cos(x)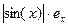

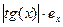
tg(x)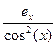

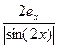
ln(x)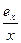

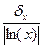
lg(x)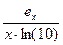

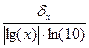
e_x e^x ∙ e_x x ∙ δ_x

10^x 10^x ∙ ln(10) ∙ e_x ln(10) ∙ e_x

x^y x^y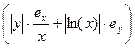

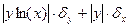
arcsin(x)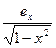

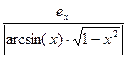
arcos(x)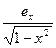

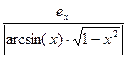
arctg(x)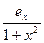

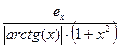
Вопросы по теме

1.Что такое абсолютная и относительная погрешности?

2.Как классифицируются виды ошибок?

3.Что значит цифра, верная в строгом, широком смыслах?

4.Как находится погрешность округленного числа?

5.Как определить количество верных цифр по относительной погрешности приближенного числа?

6.Как распространяются абсолютная и относительная погрешности в арифметических действиях?

7.Как осуществить оценку погрешности значений элементарных функций?

8.Как формулируется обратная задача теории погрешности?

9.Каковы должны быть абсолютные погрешности аргументов функции, чтобы абсолютная погрешность функции не превышала заданной величины?

10.В каких случаях используется метод границ?