Аксиоматика Цермело-Френкеля теории множеств

В § 1 приложения были даны основные понятия теории множеств. Однако развиваемая на этом основании Г. Кантором наивная теория множеств столкнулась в конце XIX в. с трудностями. Вот – лишь один пример парадокса наивной теории множеств.

Парадокс Рассела: Пусть U – множество всех множеств. Рассмотрим множество M = {A Î U | A Ï A} и попробуем ответить на вопрос: верно ли, что M Î M ? Если это утверждение истинно, т.е. M Î M, то получаем противоречие с определением множества M – оно образовано только из тех множеств, которые не являются элементами самих себя. Однако и предположение M Ï M тоже ведёт к противоречию, т.к. в этом случае (по определению множества M) должно быть выполнено M Î M. Итак, получено противоречие.

Выход из создавшейся ситуации только один – нельзя считать “множество всех множеств” U множеством: если U – не множество, то не является множеством и образованное из U с помощью конструкции выделения “множество” M, а значит, к нему не применимы дальнейшие рассуждения о множествах, и противоречие исчезает. Однако наивное изложение теории множеств не позволяет строго определить, является ли та или иная совокупность объектов множеством. Таким образом, требуется более строгий подход при определении операций над множествами.

Ниже неформально излагается система аксиом Цермело-Френкеля для формальной теории множеств, предложенная в 1908 г. Э. Цермело и усовершенствованная к 1922 г. А. Фре­н­келем. Хотя за всё время пользования этой аксиоматикой не выявлено ни одного парадокса, её непротиворечивость невозможно доказать внутренними средствами теории множеств (теорема К. Гёделя). Поэтому математики и в настоящее время не могут спать спокойно, ибо почва под их ногами постоянно колышется и даже не видно средств хоть как-то её укрепить.

Неопределяемыми понятиями теории множеств будут “множество”, “элемент”, двухместный предикат принадлежности Î и двухместный предикат равенства элементов =. Как и при построении всякой математической теории, зафиксируем алфавит теории множеств, состоящий из объектных переменных, обозначаемых большими и малыми буквами латинского алфавита, двухместных предикатных символов Î и = , логических связок Ù , Ú , ® , « , 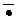, кванторов " , $ и служебных символов ( , ) –скобок. На этом этапе совокупность всех этих символов не рассматривается как множество, чтобы не возникало замкнутого круга, порочащего создаваемую теорию.

Хотя большие буквы, как правило, обозначают множества, а малые – элементы множеств, строгого разделения в обозначениях на элементы и множества не будет, ибо a’priori невозможно сказать, является ли элемент некоторого множества множеством: большие буквы будут использованы для обозначения множеств лишь в случаях, не вызывающих сомнения.

Как и в любой специальной математической теории, вводится понятие формулы теории множеств – подмножество “осмысленных” предложений в алфавите. Кроме того, введём следующие общеупотребительные сокращения: x Ï A будет обозначать 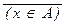, A ¹ B будет употребляться вместо 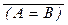, формулы (" x Î A Ф(x)) и (" x Ï A Ф(x)) – вместо (" x ((x Î A) ® Ф(х))) и (" x (x Ï A ® Ф(х))) соответственно, а ($ x Î A Ф(x)) и ($ x Ï A Ф(x)) – вместо ($ x ((x Î A) Ù Ф(х))) и ($ x (x Ï A Ù Ф(х))). Запись ($ ! x Î A P(x)) является синонимом более длинного выражения (($ x Î A P(x)) Ù (" y Î A (P(y) ® (y = x)))). В формулах теории множеств будем для краткости опускать внешние скобки, которые не несут информации.

Теперь рассмотрим аксиомы теории множеств.

1⁰. аксиома объёмности: " А, В ((А = В) « (" x (x Î A « x Î B)))

Эта аксиома говорит о том, что два множества равны тогда и только тогда, когда они имеют одинаковые элементы. В наивной теории множеств именно так определялось равенство двух множеств.

2⁰. аксиома равенства: " а, А, b ((a = b Ù a Î A) ® b Î A)

Эта аксиома согласовывает понятия равенства элементов с предикатом принадлежности: было бы странным, если бы равные элементы отличались бы принадлежностью к какому-нибудь множеству. Наивная теория множеств на такие “мелочи” внимания не обращает.

Назовём множество В подмножеством множества А, если " x (x Î В ® x Î A). В этом случае будем говорить также, что А содержит В (А включает В или А – надмножество В) и писать В Í А. Ясно, что " A, B ((А = В) « ((A Í B) Ù (B Í A)) . Для двух множеств X, Y будем писать коротко X Ì Y , если (X Í Y Ù X ¹ Y).

3⁰. аксиома выделения: " А ($ B (" x (x Î B « (x Î A Ù Р(х))))), где Р(х) – произвольная формула теории множеств со свободной переменной х, в которую не входят предметные переменные А и В.

Заметим, что при фиксированных значениях свободных переменных в формуле P(x) множество В определено однозначно: если C – другое множество, удовлетворяющее 3⁰, то " х (х Î В « (x Î A Ù P(x))) и " x (x Î C « (x Î A Ù P(x))), так что " x ((x Î В) « (x Î C)), т.е. B = C по аксиоме объёмности. Множество В будет в дальнейшем обозначаться через {x Î A | P(x)}. Ограничение, накладываемое на формулу P(x) существенно ограничивает возможности принципа выделения.

Из аксиомы выделения следует, в частности, существование множества, не имеющего элементов, которое называется пустым множеством, и будет обозначаться символом Æ .Его можно задать, например, так: Æ = {x Î A | x ¹ x}, где А – любое множество. Легко понять, что пустое множество определено однозначно: если Е – любое множество без элементов, то " х (х Î Е « x Î Æ) и, по аксиоме объёмности, Е = Æ .

Кроме того, аксиома выделения позволяет построить пересечениеи разность двух множеств: А Ç B = {x Î A | x Î B} , A \ B = {x Î A | x Ï B}. Следует отметить, что эти множества корректно определены, если A и B – разные буквы. Если же A = B, то дополнительно нужно положить А Ç A = A, A \ A = Æ. Аксиома выделения не позволяет образовать объединение двух множеств A È B = {x Î ? | x Î A Ú x Î B}, т.к. не известно, из какого множества нужно брать элементы объединения. В то же время, если A Í C, B Í C для некоторого множества C, то по аксиоме выделения уже можно создать объединение A È B = {x Î С | x Î A Ú x Î B}.

4⁰. аксиома существования булеана(множества всех подмножеств) :

" A ($ B (" X (X Î B « X Í A)))

Введённое множество В будем в дальнейшем обозначать через В(А) и называться булеаном множества А или множеством всех подмножеств множества А. Проверьте самостоятельно, что булеан определён однозначно.

5⁰. аксиома (неупорядоченной) пары:

" а, b ($ A (" x (x Î A « (x = a Ú x = b))))

Содержательно здесь говорится о возможности образовывать множество А = {a, b}, состоящее излюбых объектов а, b. Построенное множество тоже определено однозначно (?!). Оно не обязательно двухэлементно: если а = b, то {a, b} содержит один элемент, и в этом случае будет обозначаться просто через {a}.

Эта аксиома позволяет ввести понятие упорядоченной пары– математического объекта (a; b), удовлетворяющего следующему свойству упорядоченной пары " а, b, c, d (((a; b) = (c; d)) ® ((a = b) Ù (c = d))). Именно, назовём упорядоченной парой объектов а и b множество (a; b) = {{a}, {a, b}}, существование которого гарантируется аксиомой (неупорядоченной) пары. Проверим, что при этом выполняется свойство упорядоченной пары. В самом деле, согласно аксиомам объёмности и неупорядоченной пары, если {{a}, {a, b}} = {{c}, {c, d}} , то возможны следующие случаи:

1) {a} = {c}. Тогда а = с. Если при этом {a, b} = {c, d} , то {a, b} = {а, d} и b = d (возможно, b = a = d).Если же {a, b} = {с}, то a = c = b и {a} = {a, b} = {с, d}, т.е. {a, d} = {a}, и последнее равенство опять даёт b = a = d , что и требовалось.

2) {a} ¹ {c}, т.е. a ¹ c. Тогда {a} = {c, d}, что невозможно, т.к. с Ï {a} .

Итак, определено понятие упорядоченной пары, которое не задаёт объект “упорядоченная пара” однозначно: например, множество {{{a}, {a, b}}} тоже удовлетворяет свойству упорядоченной пары. Проверьте это и придумайте другие упорядоченные пары. Всюду далее обозначение (a; b) будет означать, что (а, b) = {{a}, {a, b}}.

6⁰. аксиома объединения: " А ($ U (" х (х Î U « ($ C (C Î A Ù x Î C)))))

Множество U состоит из всех элементов, принадлежащих хотя бы одному множеству, являющемуся элементом множества А.

Эта аксиома значительно сильнее, чем утверждение о существовании объединения двух множеств: она постулирует существование объединения U всех множеств, входящих в качестве элементов в заданное множество А. Построенное множество U определено однозначно (?!), называется объединением по Аи обозначается через È {C Î A} или .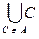

Теперь с помощью аксиомы выделения можно определить для множества А и пересечение по А, полагая Ç {C Î A} = {x Î È {C Î A} | " C Î A x Î C}. Это множество состоит из всех элементов, принадлежащих одновременно всем множествам, являющимся элементами множества А и обозначается также через .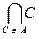

Упражнение.Чему равно объединение и пересечение по пустому множеству ?

Как теперь построить объединение двух множеств А и В ? Рассмотрим неупорядоченную пару P = {A, B} и применим к ней аксиому объединения. Тогда множество È {C Î P} и будет объединением множеств А и В, которое в дальнейшем будет обозначаться просто через А È В : по аксиоме объединения " x ((x Î È {C Î {A, B}}) « « (x Î A Ú x Î B)), что и требовалось.

С помощью конструкций пересечения и объединения двух множеств можно построить пересечение и объединение любого конечного числа множеств:

A₁ Ç ... Ç A_n = ((...(A₁ Ç A₂) Ç ... ) Ç A_n–1) Ç A_n ,

A₁ È ... È A_n = ((...(A₁ È A₂) È ... ) È A_n–1) È A_n .

Если теперь а₁ , ... , а_n – произвольные элементы, то по аксиоме пары, существуют множества {a₁}, ... , {a_n}, объединение которых, даёт конечное множество {a₁ , ... , a_n } .

Если А и В – множества, а Î А, b Î B, то можно спросить – какому множеству принадлежит упорядоченная пара (а; b) = {{a}, {a, b}} ? Ясно, что {a} Î B(A È B) , {a, b} Î B(A È B), поэтому (а; b) Î B(B(А È В)). Теперь можно применить аксиому выделения, чтобы построить декартово произведение

A´В = {x Î B(B(A È B)) | ($ a ($ b (a Î A Ù b Î B Ù x = (a; b))))} .

Так как упорядоченная пара существует для любых объектов, то А´В = Æ тогда и только тогда, когда А = Æ или В = Æ .

Упражнение.Докажите следующие свойства декартова произведения:

1) А´В Í С´D тогда и только тогда, когда А Í С и В Í D ,

2) А´В = С´D тогда и только тогда, когда А = С и В = D ,

3) А´(В´С) = (А´В)´С тогда и только тогда, когда А = С = Æ .

7⁰. аксиома регулярности: " А ¹ Æ ($ В Î А (" а Î А а Ï В))

Содержательно эта аксиома говорит о том, в любом непустом множестве A существует элемент В Î А, не содержащий никаких элементов из А.

Важное следствие этой аксиомы заключается в том, что не существует множеств А, В со свойством А Î В Î А : если бы нашлись такие множества, то множество-пара {A, В} не удовлетворяла бы аксиоме регулярности, т.к. любой из его элементов содержит хотя бы один элемент множества {A, В}, т.к. А содержит В, а В содержит А.

В частности, не существует множества, содержащего себя в качестве элемента, ибо если А Î А, то А Î А Î А, вопреки доказанному. Это ставит вне закона “множество всех множеств”, ибо такой объект должен содержать как элемент сам себя.

Кроме того, аксиома регулярности позволяет решать и некоторые другие вопросы. Например, с её помощью можно доказать, что равенство а = (а; b) невозможно: если допустить, что а = (а; b) = {{a}, {a, b}}, то а Î {a} Î a , что невозможно.

Упражнения: 1.Докажите, что объект {a, {a, b}} также удовлетворяет свойству упорядоченной пары.

2.Докажите, что не существует множеств А, В, С со свойством А Î В Î С Î А.

3.Обобщите предыдущее упражнение на случай произвольного числа множеств.

Введём теперь понятие функции f : ? ® ? с неопределёнными областями определения и значений, понимая под этим любое множество f, удовлетворяющее следующему обобщённому условию функциональности:

(" х Î f ($ u, v x = (u; v))) Ù (" u, v, w ((u; v) Î f Ù (u; w) Î f) ® v = w).

При этом если (u; v) Î f, то будем кратко писать f(u) = v и называть v значением функции f на элементе u .

Следует отметить, что для функции f с неопределёнными областями определения и значений нельзя применить аксиому выделения для построения области её определения и множества значений. Например, пытаясь задать Im(f) = { b Î ? | $ a (a; b) Î f}, невозможно указать из какого множества выбирать значения b. Поэтому необходима специальная аксиома, присваивающая статус множества этому объекту.

8⁰. аксиома существования области значений: для любой формулы Ф(х, у) со свободными переменными х, у справедливо свойство

" А (" х Î A (" у, z (Ф(х, у) Ù Ф(х, z) ® y = z))) ® ($ B(" y (y Î B « ($ x Î A Ф(х, у)))))

Эта аксиома имеет дело с более широким классом зависимостей, чем обычные функции: она утверждает существование “области значений” В = Im_А (Ф) для любого функционального на Азакона, выражаемого с помощью формулы Ф(х, у), даже в том случае, если a’priori неизвестно, определяет ли Ф функцию на А (ведь пока не ясно, будет ли множеством объект {(x; y) Î ? | x Î A Ù Ф(х, у)}).

Теперь можно с полным основанием ввести области значений и определения функции f с неопределёнными областями определения и значений на заданном множестве А: нужно только заметить, что формула Ф(х, у) = ((х; у) Î f) функциональна на А, т.е. удовлетворяет посылке аксиомы существования области значений. Значит, определено множество Im_А (f) = Im_А (Ф), состоящее из всех тех у,для которых найдётся х Î А со свойством (х; у) Î f . Поэтому по аксиоме выделения можно ввести область определения функции f на множестве А – множество D_А (f) = {a Î A | $ b Î Im_А (f) (a; b) Î f}. Если D_А (f) = A, то будем называть функцию f отображением на А.

Узаконив функции, можно определить индексированные элементами одного множества последовательности: если I – множество, то говорят, что задана последовательность объектов а_i , где i Î I, если задана функция а : I ® ?, где а_i = a(i). Ясно, что можно рассматривать множество всех членов последовательности, поскольку оно является областью значений функции а: {a_i}_iÎI = Im_I (a).

Возникает вопрос, зачем нужны функции с неопределёнными областями определения и значений ? Дело в том, что если A и B – два множества, то можно было бы определить понятие функции из A в B как любое множество f (обычно обозначаемое через f : A ® B), удовлетворяющее свойству функциональности:

(" х Î f ($ u Î A ($ v Î B x = (u; v)))) Ù (" u Î A " v, w Î B ((u; v) Î f Ù (u; w) Î f)) ® v = w).

Для таких функций области значений и определения существуют просто по аксиоме выделения: Im(f) = {b Î B | $ a Î A (a; b) Î f}, D(f) = { a Î A | $ b Î B (a; b) Î f}.

Значение аксиомы существования области значений состоит в том, что она даёт средство с помощью формул теории множеств, обладающих свойствами функциональности получать универсальные задания “функций”, определённых на всех мыслимых множествах сразу. Действительно, для любой формулы Ф(х, у) со свойством функциональности можно рассмотреть объект f = {(a; b) Î A´Im_А (Ф) | Ф(a, b)} являющийся множеством согласно аксиоме выделения. (Это описание не слишком формально. Вставьте в него определение декартова произведения А´Im_А (Ф) и сформулируйте строго условие, которому должна удовлетворять формула Ф(x, y)). Таким образом, на каждом множестве А рассматриваемая формула определяет функцию, но задана эта функция сразу для любого мыслимого множества.

Например, можно определить ординальные числаили ординалы как множества из “область истинности” следующего универсального “предиката”-формулы:

Ord(X) = (" Y, Z ((Z Î Y Ù Y Î X) ® Z Î X))) Ù (" Y, Z Î X (Z Î Y Ú Y = Z Ú Y Î Z)).

“Предикат” Ord является конъюнкцией двух условий: транзитивности относительно Î и линейной упорядоченности относительно Î .

На самом деле, конечно, говорить о предикате Ord и о его области истинности можно, только ограничив действие Ord на некотором фиксированном множестве А, т.е. для соблюдения формальностей нужно ввести формулу Ф(х, у) = (у Î х Ù Ord(y)) и воспользоваться аксиомой существования области значений для получения множества Im_А (Ф) всех ординальных чисел из множества А. Это соответствует описанной выше общей схеме использования аксиомы существования области значений.

9⁰. аксиома бесконечности: $N (Æ Î N) Ù (" X Î N X È {X} Î N)

Эта аксиома впервые утверждает существование некоторого множества. До сих пор все конструкции множеств “повисали в воздухе”, поскольку не было ясно, существует ли хотя бы одно множество. Интуитивно ясно, что множество N должно быть бесконечным, т.к. оно содержит попарно различные элементы n₀ = Æ , n₁ = Æ È {Æ}, n₂ = Æ È {Æ} È {Æ È {Æ}},и.т.д.

Упражнение.Упростите вид элементов n₁ , n₂ , n₃ , … , n_i , … и докажите, что все они попарно различны.

Говорят, что два множества X и Y равномощны, если существует биективное отображение (биекция) Х на Y, т.е. такая функция f: X ® Y, для которой D(f) = X, Im(f) = Y и выполнено условие инъективности " a, b Î X (f(a) = f(b) ® a = b). В этом случае пишут кратко X » Y.

Примеры: 1. Z » 2·Z » N.

Здесь, как обычно, 2·Z = {x Î Z | $ z Î Z x = 2·z}. Можно взять следующие отображения f : Z ® 2·Z, где f(z) = 2·z, j : N ® Z, где j(n) = .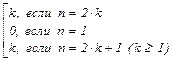

Легко понять, что f и j – биекции, и воспользоваться следующим примером.

2.А » А ; если А » В, то В » А; если А » В и В » С, то А » С. Эти три свойства – рефлексивность, симметричность и транзитивность отношения равномощности.

Достаточно рассмотреть биекции id_A : A ® A – тождественное отображение множества А, f ^–1 : B ® A, где f : A ® B – биекция, и g o f : A ® C, где f : A ® B и g : B ® C – биекции.

Эти примеры неформальны, т.к. множества натуральных чисел N, как и множества Z целых чисел и Q рациональных чисел ещё не построены.

Формализуем теперь понятия конечного и бесконечного множеств. Множество А называется бесконечным, если оно равномощно некоторому своему собственному подмножеству, и конечным, если оно не является бесконечным. Эти определения можно записать формально в несколько этапов:

(A – бесконечно) º ($ B Æ ¹ B ¹ A) Ù ($ f : A ® B – би),

($ B Æ ¹ B ¹ A) º ($ B ($ b Î B) Ù ($ a Î A a Ï B)),

($ f : A ® B – би) º ($ f : A ® B – функция) Ù (D(f) = A) Ù (Im(f) = B) Ù (f – инъ),

($ f : A ® B – функция) º ($ f (" u Î f ($ a Î A ($ b Î B u = (a; b))))) Ù (f – функционально),

(f – функционально) º (" a Î A (" b, c Î B (((a; b) Î f Ù (a; c) Î f) ® b = c))),

(D(f) = A) º (" a Î A ($ b Î B (a; b) Î f)),

(Im(f) = B) º (" b Î B ($ a Î A (a; b) Î f)),

(f – инъ) º (" x, y Î A ($ z Î B ((x; z) Î f Ù (y; z) Î f) ® x = y)).

Условие бесконечности множества А можно теперь записать в виде формулы, последовательно подставив все приведённые фрагменты в самую первую из квазиформул. Взяв отрицание этой формулы, получим в виде формулы условие конечности множества А.

Упражнение. Совпадает ли введённое новое понятие конечного множества с прежним понятием конечного множества {a₁ , … , a_n} ?

Теперь можно выделить “натуральные числа” из бесконечного множества N . Для этого запишем квазиформулу, задающую “натуральные числа”:

Nat(y) = (Ord(y) Ù (" zÎ y (z = Æ Ú ($ t z = t È {t}))) Ù (y – конечно))

и снова воспользуемся аксиомой существования области значений для формулы Ф(х, у) = (у Î х Ù Nat(у)), чтобы получить множество N всех “натуральных чисел”, принадлежащих бесконечному множеству N. При этом элементы Æ , Æ È {Æ}, Æ È {Æ} È {Æ È {Æ}} , … множества N в дальнейшем обозначаем через 1, 2, 3, … , отождествляя их с “обычными” натуральными числами.

Упражнения. 1.Докажите, что для любого конечного множества А и произвольного объекта b множество A È {b} конечно. Выведите отсюда, что для любого n Î N множество {a₁ , … , a_n } конечно.

3.Докажите бесконечность построенного множества N.

4.Докажите, что множество, содержащее бесконечное подмножество, само бесконечно.

5.Докажите, что N, Z и Q равномощны, как равномощны R и R´R.

6.Проверьте условие функциональности для Ф(х,у) = у Î х Ù Nat(у) .

7.Докажите, что множество N = {n Î N | Nat(n)} является ординалом и что это – первый бесконечный ординал (обозначаемый обычно через w), в котором содержатся все конечные ординалы Æ , Æ È {Æ}, Æ È {Æ} È {Æ È {Æ}} , … .

Может возникнуть резонный вопрос: откуда такие определения конечных и бесконечных множеств ? Докажем неформально следующую теорему:

Теорема (об эквивалентных понятиях конечности (бесконечности) множеств).Следующие условия эквивалентны:

(1) либо А = Æ , либо A = {a₁ , … , a_n },

(2) A не содержит последовательности {x_i}_{i Î N} со свойством x_i ¹ x_j при i ¹ j,

(3) A конечно.

Эквивалентны и следующие условия:

(1¢) А ¹ Æ и не представимо в виде А = {a₁ , … , a_n },

(2¢) A содержит последовательность {x_i}_{i Î N} со свойством x_i ¹ x_j при i ¹ j,

(3¢) А бесконечно.

Доказательство. Прежде всего, отметим, что если множество A бесконечно, т.е. существует биекция f : A ® B на собственное подмножество Æ ¹ B ¹ A, то множество B тоже бесконечно. Действительно, отображение f можно рассматривать как отображение на свой образ: f : B ® f(B) = {c Î B | $ b Î B c = f(b)}. Проверим, что f(B) – собственное подмножество в B. Ясно, что Æ ¹ f(B) Í B. Если f(B) = B и a Î A \ B, то f(a) Î B и найдётся b Î B со свойством f(b) = f(a), откуда ввиду инъективности f получим a = b Î B, что невозможно.

(1) Þ (2) Для А = Æ утверждение (2) очевидно. Если A = {a₁ , … , a_n }, то " x Î A (x = a₁) Ú (x = a₂ ) Ú … Ú (x = a_n). Поэтому существование последовательности {x_i}_{i Î N} со свойством x_i ¹ x_j при i ¹ j приводит к противоречию: среди первых её n членов содержатся все элементы множества A.

(2) Þ (3) Пусть A не содержит последовательности элементов {x_i}_{i Î N} со свойством x_i ¹ x_j при i ¹ j. Если А не конечно, то оно бесконечно, т.е. равномощно своему собственному подмножеству B. Приведём это предположение к противоречию. В частности, A ¹ Æ, т.к. Æ ¹ A \ B Í A. Выберем элемент x₁ Î A. Предположим, что уже построено множество {x₁ , … , x_k } попарно различных элементов множества А.

Если А ¹ {x₁ , … , x_k }, то в непустом множестве A \ {x₁ , … , x_k } можно выбрать элемент x_k+1 , который не совпадает ни с одним из элементов x₁ , … , x_k , и получить новое множество {x₁ , … , x_k , x_k+1 } попарно различных элементов. Если эта процедура продолжится сколь угодно долго, то будет построена последовательность {x_i}_{i Î N} попарно различных элементов, вопреки (2).

Значит, на некотором шаге, получим А = {x₁ , … , x_k }. Проверим, что это множество конечно, вопреки допущению о бесконечности множества А. Если существует биекция f : {x₁ , … , x_k } ® B на некоторое собственное подмножество B Ì {x₁ , … , x_k }, то B бесконечно, т.е. f(B) Ì B. Поэтому получим убывающую цепь бесконечных множеств: {x₁ , … , x_k } = A É B É B₁ = f(B) É … É B_k–1 = f(B_k–2) É … , что невозможно, ибо множество B_k–1 уже будет пустым (на каждом шаге включения строгие).

(3) Þ (1) Пусть A ¹ Æ и А конечно. Рассуждая аналогично доказательству (2) Þ (3), во множестве А построим последовательностьэлементов X = {x_i}_{i Î N} со свойством x_i ¹ x_j при i ¹ j . Зададим функцию f : A ® A \ {x₁} следующим образом: f(a) = 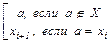. Нетрудно проверить, что это отображение биективно, вопреки конечности множества A.

Эквивалентности (1¢) Û (2¢) Û (3¢) доказываются аналогично. Теорема доказана.

10⁰. аксиома выбора: " Х ((" Y Î X Y ¹ Æ )® ($ M (" YÎ X ($ ! m Î M Ç Y)))))

Посылка этой аксиомы говорит о том, что множество Х состоит из непустых множеств, а заключение утверждает, что в каждом из этих множеств можно выбрать по одному представителю и образовать из них некоторое множество М.

Центр тяжести здесь не в утверждении о возможности выбора в каждом множестве Y Î X одного элемента (это очевидно, т.к. Y ¹ Æ), а в том, что выбранные элементы образуют множество. Таким образом, аксиома выбора является ещё одним средством конструирования множеств.

Эта аксиома эквивалентна (при выполнении предыдущих аксиом теории множеств) следующему утверждению: для любого множества Х, состоящего из непустых множеств, существует функция f : X ® È {Y Î X} со свойством " Y Î X f(Y) Î Y, называемая функцией выбора. В са­мом деле, если верна аксиома выбора, то для построения искомой функции достаточно положить f = {(Y; m) Î X´M | m Î M Ç Y} поаксиоме выделения и убедиться в выполнении условия функциональности для f . Обратное утверждение тоже доказывается просто: если есть функция выбора, то в качестве M достаточно взять её образ Im(f).

Отметим ещё, что условие (" Y Î X Y ¹ Æ ) аксиомы выбора выполнены для множества X = B(A) \ Æ для любого непустого множества A. Таким образом, из аксиомы выбора следует утверждение " A ¹ Æ ($ M (" Y Î B(A) \ Æ ($ ! m Î M Ç Y))), обеспечивающее существование множества представителей непустых элементов булеана. Оказывается, что это утверждение эквивалентно аксиоме выбора. Действительно, если задано множество X из непустых подмножеств, то его элементы будут элементами множества B(È{Y Î X}) \ Æ, так что существует такое множество представителей M, что " Y Î B(È{Y Î X}) \ Æ ($ ! m Î M Ç Y). В частности, это условие выполнено и для любого Y Î X.

Рассматриваемая аксиома очевидна, когда все, участвующие в ней множества конечны, она может быть доказана для любого конечного множества Х,но в общем случае высказанное в ней утверждение далеко неочевидно. Чтобы прояснить ситуацию (а может быть, окончательно запутать ?), представим, что Дед Мороз решил пересчитать подарки в своём мешке. Как он должен поступить ? Вытаскивать кульки по одному из мешка и, считая, отдавать их Снегурочке, пока мешок не опустеет. Предположим теперь, что Снегурочка, не желая ненароком рассыпать кульки, возвращает каждый кулёк обратно Деду Морозу, привязывая к нему бантик. Тогда Дед Мороз тоже сможет пересчитать подарки, ощупывая каждый вытаскиваемый кулёк, чтобы дважды не вытащить один и тот же, до тех пор, пока в мешке не останутся только кульки с бантиками. Наконец, предположим, что выключился свет, а Снегурочка не умеет завязывать бантики в темноте. Тогда Дед Мороз не сможет пересчитать свои подарки. Аналогичная ситуация и в теории множеств: мешок Деда Мороза – это множество Х, подарки – его элементы Y Î X, а роль Снегурочки исполняет функция выбора, которая “привязывает” к каждому подарку Y бантик f(Y) = m Î M Ç Y. Отличие только в том, что аксиома выбора позволяет математикам и в полной темноте пересчитать подарки Деда Мороза. В этом и её неочевидность, ибо Деду Морозу невозможно объяснить – как же всё-таки осуществлять выбор подарков в темноте… Этот пример показывает также тесную связь между процессами выбора и упорядочивания: пересчёт ведёт к упорядочиванию. Как покажет приведённая ниже теорема, связь эта глубока и далеко не случайна.

Аксиома выбора многократно использовалась математиками неявно, пока Э. Цермело не придал ей точную формулировку. Кстати, доказательство предыдущей теоремы тоже опирается на аксиому выбора: выделенная жирным фраза в её доказательстве не может быть обоснована без аксиомы выбора. В ней говорится, что если для каждого натурального n построены функции f_i : {1, … , n} ® A, определяющие члены последовательности x₁ , … , x_i (и поэтому удовлетворяющие свойствам f_i(k) = x_k (1 £ k £ i) при любом i Î N), то существует и функция f : N ® A, определяющая сразу всю последовательность {x_i}_{i Î N} , т.е. f(n) = x_n при любом n Î N. Строгое доказательство этого факта требует использования аксиомы выбора.

Обсуждение последовавших вслед за явлением миру аксиомы выбора жарких математических дискуссий оставим без комментариев, а пока для иллюстрации приведём несколько эквивалентных формулировок этой аксиомы, напомнив предварительно некоторые понятия, связанные с отношениями порядка на множествах.

Пусть А – непустое множество. Говорят, что ρ – бинарное отношение на А, если ρ – непустое подмножество в А´А . При этом для упорядоченной пары (а; b) вместо (а; b) Î ρ пишут просто a ρ b .

Бинарное отношение £ на множестве А называется частичным порядком на А, если это отношение удовлетворяет трём условиям: 1) рефлексивность " а Î А а £ а , 2) антисимметричность " а, b Î A a £ b Ù b £ a ® a = bи 3) транзитивность " a, b, c Î A a £ b Ù b £ c ® a £ c. Частичный порядок £ называется линейным, если " а, b Î A (a £ b) Ú (b £ a). Частично упорядоченное множество (ч.у.м.)– это упорядоченная пара (А, £), где А – непустое множество, а £ – некоторый фиксированный частичный порядок на А. Для произвольного элемента а Î А назовём начальными отрезками множества А множества вида А_а = {x Î A | x £ a Ù x ¹ a}. Если (А, £) – частично упорядоченное множество, то любое его собственное подмножество Æ ¹ М Í А можно рассматривать как ч.у.м. (М, £) с тем же отношением порядка £ , что и в А . Произвольное линейно упорядоченное подмножество (M, £) частично упорядоченного множества (А, £) называется цепью.

Если M – подмножество ч.у.м. A, то любой элемент а Î А со свойством " m Î M m £ a называется верхней гранью множества М. Элемент m Î M называется минимальным (соответственно максимальным) элементом множества М, если " x Î M 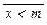(соответственно " x Î M 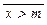). Если " x Î M m £ x (или " x Î M x £ m), то элемент m Î M называется наименьшим (соответственно наибольшим) элементом множества М. В случае линейного порядка понятия минимального и наименьшего (соответственно максимального и наибольшего) элементов совпадают, но в частично упорядоченном множестве условия 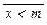и x ³ m (как 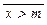и x £ m) не эквивалентны (?!).

Говорят, что линейный порядок £ на ч.у.м. (А, £) является полным порядком, если любое непустое подмножество М Í А имеет наименьший элемент. Само множество (А, £) при этомназывают вполне упорядоченным (в.у.м.). Если на множестве Х можно определить некоторое отношение линейного (полного) порядка, то говорят, что множество Х можно линейно (соответственно вполне) упорядочить. Отметим, что любое подмножество В вполне упорядоченного множества (А, £) само вполне упорядочено: действительно, если М – непустое подмножество в В, то оно обладает наименьшим элементом как подмножество в А. Кроме того, для каждого элемента а вполне упорядоченного множества (А, £) однозначно определён непосредственно следующий за ним (по порядку £) элемент а₊ = min{xÎ A | x > a}. В противоположность этому, непосредственно предшествующий элемент определён не всегда: например, во вполне упорядоченном множестве (N È {+ 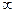}, £) с естественным порядком £ у элемента +∞ нет непосредственно предшествующего.

Примеры: 1.Множества N, Z, Q, R линейно упорядочены обычным отношением порядка £ . При этом на множестве N этот порядок является полным, а на остальных множествах – нет, т.к. их общее подмножество Z Í Q Í R не обладает минимальным элементом.

2.Для любого множества А бинарное отношение Х Í Y является отношением частичного порядка на булеане В(А). Этот порядок будет линейным только для одноэлементного или пустого множества А. При этом каждая цепь С – это элемент из В (В(А)), состоящий из элементов X Î В(А), линейно упорядоченных по включению Í . Каждая цепь С имеет верхнюю грань È{c Î C} в В(А): " с Î С с Í È{c Î C}.

3.Функция f : A ® B является подмножеством булеана B(A´B). При этом для функции g : A ® B выполняется включение f Í g тогда и только тогда, когда g – продолжение функции f , т.е. D(f) Í D(g) и " а Î D(f) g(a) = f(a). Поэтому каждая цепь С функций из А в В имеет функцию È{c Î C} в качестве верхней грани (проверьте, что È{c Î C} будет функцией, если функцией является каждый элемент c Î C).

4. Подмножество М = {{1, 3}, {1, 2}, {2, 3}} булеана (B({1, 2, 3}), Í) не содержит цепей, имеет три минимальных и три максимальных элемента, но ни одного наименьшего и наибольшего. Всё множество {1, 2, 3} (и только оно) является верхней гранью М в B({1, 2, 3}).

Доказательство следующей теоремы при первом чтении можно опустить, хотя нужно учесть, что оно богато идеями и стандартными техническими приёмами, част