А теперь рассмотрим критерии исключения грубых погрешностей или промахов.
При однократных измерениях обнаружить промах не представляется возможным. Для уменьшения вероятности появления промахов измерения необходимо повторять достаточное число раз, а за результат принять среднее арифметическое этих измерений. Для обнаружения промахов используют статистически критерии, предварительно определив, какому распределению вероятности соответствуют результаты выполняемых измерений.
Вопрос о том, содержит ли результат наблюдения грубую погрешность, решается общими методами про верки статистических гипотез. Проверяемая гипотеза состоит в утверждении, что результат наблюдения не содержит грубой погрешности, т.е. является одним из значений измеряемой величины. Пользуясь определенными статистическими критериями, пытаются опровергнуть выдвинутую гипотезу. Если это удается, то результат наблюдений рассматривают как содержащий грубую погрешность и его исключают. Эта общая схема действий, которую далее мы дополним конкретными алгоритмами действий.
Для выявления грубых погрешностей задаются вероятностью q, которая определяет уровень значимости того, что сомнительный результат действительно мог иметь место в данной совокупности результатов измерений.
Критерий «трех сигм»применяется для результатов измерений, распределенных по нормальному закону. Поэтому критерию считается, что результат, возникающий с вероятностью q ≤0,003, маловероятен, и его можно считать промахом. При этом величины математического ожидания физической и среднеквадратичного отклонения вычисляют без учета экстремальных значений. Данный критерий надежен при числе измерений больших 20.
Критерий Романовского применяется в случае, если число измерений меньше 20. При этом вычисляется отношение 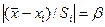 и сравнивается с критерием βт, (табличным значением) выбранным по таблице 1. Если β ≥ βт то результат хi считают промахом и отбрасывают.
и сравнивается с критерием βт, (табличным значением) выбранным по таблице 1. Если β ≥ βт то результат хi считают промахом и отбрасывают.
Таблица 1
Уровень значимости βт = f(n)
| Вероят-ность q | Число измерений | ||||||
| n=4 | n=6 | n=8 | n=10 | n=12 | n=15 | n=20 | |
| 0,01 0,02 0,05 0,10 | 1,73 1,72 1,71 1,69 | 2,16 2,13 2,10 2,00 | 2,43 2,37 2,27 2,17 | 2,62 2,54 2,41 2,29 | 2,75 2,66 2,52 2,39 | 2,90 2,80 2,64 2,49 | 3.08 2,96 2,78 2,62 |
Вариационный критерий Диксона — удобный и достаточно мощный с малыми вероятностями ошибок. При его применении полученные результаты наблюдений записывают в вариационный возрастающий ряд х1, х2,..., хn (х1<х2<... <хn).Критерий Диксона определяется как
Кд =(хn –хn-1)/(хn –x1).
Критическая область для этого критерия Р (Кд > Zq) = q. Значения Zq помещены в табл.2
Таблица 2
Дата добавления: 2020-03-17; просмотров: 1075;











