Погрешность округленного числа

Пример 1.9.

Округляя число х = 1,1426 до четырех значащих цифр, определить абсолютную и относительную погрешности полученных приближений. Цифры верны в широком смысле.

Решение.

Округлим число х до четырех значащих цифр: х₁ = 1,143.

По определению верной цифры в широком смысле абсолютная погрешность е_х = 0,0001.

Погрешность округленного числа равна сумме погрешности исходного числа и погрешности округления.

Δ_окр = │1,143 – 1,1426│ = 0,0004;

е_х 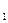= 0,0004 + 0,0001 = 0,0005;

δ_х = 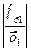= = 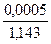0,000437 < 0,04 %.

Пример 1.10.

Число х, все цифры которого верны в строгом смысле, округлить до трех значащих цифр. Для полученного результата х₁ вычислить границы абсолютной и относительной погрешностей. В записи числа х₁ указать количество верных цифр по абсолютной и относительной погрешностям х = 1,1426.

Решение примера 1.10. представлено на рис. 1.2.

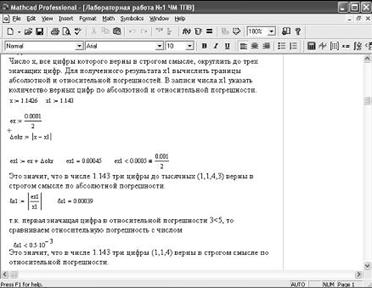
Рис. 1.2. Фрагмент рабочего документа к выполнению примера 1.10

Пример 1.11.

Со сколькими верными в строгом смысле десятичными знаками после запятой нужно взять:

а) ;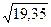

б) sin(0.9);

в) ;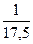

г) ln(1.25), чтобы относительная погрешность не превышала 0,1%.

Решение.

а) 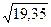= 4,3931765.

Относительная погрешность δ_х ≤ 0,001 = 10^-3. Значит, число 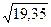, по крайней мере, имеет две верные в строгом смысле цифры.

Δх = 4,3931765 ∙ 10^-3 = 0,00439 < 0,005. Следовательно, цифры 4 и 3 действительно верны в строгом смысле, поэтому правильный ответ 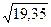≈ 4,39.

б) sin(0.9) = 0.7833269.

Относительная погрешность δ_х ≤ 0,001 = 10^-3. Значит, число sin(0.9), по крайней мере, имеет две верные в строгом смысле цифры.

Δх = 0,7833269 ∙ 10^-3 = 0,000733 >0,0005. Следовательно, цифры 5, 7 и 3 действительно верны в строгом смысле, поэтому правильный ответ sin(0,9) = 0,783

в) 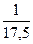= 0,0571429.

Относительная погрешность δ_х ≤ 0,001 = 10^-3. Значит, число 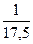, по крайней мере, имеет две верные в строгом смысле цифры.

Δх = 0,0571429 ∙ 10^-3 = 0,000057 > 0,00005. Следовательно, цифры 5 и 7 действительно верны в строгом смысле, поэтому правильный ответ 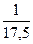= 0,057.

г) ln(1.25) = 0,223144.

Относительная погрешность δ_х ≤ 0,001 = 10^-3. Значит, число ) ln(1.25), по крайней мере, имеет две верные в строгом смысле цифры.

Δх = 0,223144 ∙ 10^-3 = 0,00022 < 0,0005. Следовательно, цифры 2, 2, 3, 1 действительно верны в строгом смысле, поэтому правильный ответ ln(1.25) = 0,2231.