Погрешности арифметических действий

Пример 1.12.

Найти сумму приближенных чисел, абсолютные погрешности которых даны. В ответе сохранить верные цифры и одну сомнительную.

х = 7,12 ± 0,01, у = 8,27 ± 0,01.

Решение.

Найдем сумму данных чисел х + у = 7,12 + 8,27 = 15,39.

Для определения количества верных цифр найдем абсолютную погрешность суммы е_х+у = 0,01 + 0,01 = 0,02. Данное число показывает, что в числе 15,39 верными будут цифры до разряда десятых, т. е. цифры 1, 5 и 3. И т. к. мы отбрасываем число 9, большее пяти, то результат сложения будет 15,4.

По относительной погрешности можно получить более строгую оценку количества верных цифр:

δ_х+у = 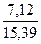∙ 0,0014 + 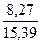∙ 0,0012 = 0,0012 < 0,5 ∙ 10^-2.

То есть в числе 15,39 цифры 1, 5 верны в строгом смысле.

Ответ: 15.

Пример 1.13.

Найти разность чисел, цифры которых верны в строгом смысле. В ответе сохранить верные цифры и одну сомнительную.

х = 13,876, у = 11,82.

Решение.

Так как цифры данных чисел верны в строгом смысле, то их абсолютные погрешности не превосходят единицы разряда, в котором записана последняя верная цифра. Поэтому е_х = 0,0005, е_у = 0,005.

Относительная погрешность чисел х и у соответственно равна:

δ_х = 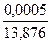= 0,00004;

δ_у = = 0,0004.

Найдем разность чисел х – у = 13,876 – 11,82 = 2,056.

Найдем абсолютную погрешность полученной разности. Она будет равна

е_х-у = 0,0005 + 0,005 = 0,0055 < 0,05.

То есть в числе 2,056 цифры 2 и 0 верны в строгом смысле.

Найдем относительную погрешность разности. Она будет равна

δ_х-у = 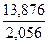∙ 0,00004 + 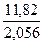∙ 0,0004 = 0,0025 ≤ 0,5 ∙ 10^-2.

Действительно, две первые цифры верны в числе 2,056.

Ответ: 2,06.