Погрешности элементарных функций

Пример 1.14.

Исходные числовые значения аргумента заданы цифрами, верными в строгом смысле. Найти абсолютную и относительную погрешности функции. Определить количество верных цифр в строгом смысле по относительной погрешности в следующих элементарных функциях:

а) cos(0,47);

б) у = е^-3,1;

в) у = ;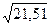

г) у = ln(68,214).

Решение.

а) Находим значение величины х. Оно будет равно 0,891568.

Абсолютная погрешность аргумента е_0,47 = 0,005.

Тогда абсолютная и относительная погрешности величины х равны:

е_cos(0,47) = │sin(0.47)│ ∙ 0.005 = 0,00226443;

δ_cos(0,47) = │tan(0.47)│ ∙ 0.005 = 0,00253983 ≤ 0.005 = 0,5 ∙ 10^-2.

Это означает, что в числе 0,891568 две цифры после запятой верны в строгом смысле.

Ответ: 0,892.

б) Находим значение величины у. Оно будет равно 0,0450492.

Абсолютная погрешность аргумента е_у = 0,05. Тогда абсолютные и относительные погрешности величины у равны:

е_х = │е^-3,1│ ∙ 0,05 = 0,0225246;

δ_у = 0,05 = 0,5 ∙ 10^-1.

Это означает, что в числе 0,0450492 одна цифра после запятой верна в строгом смысле.

Ответ: 0,04.

в) Находим значение величины у. Оно будет равно 4,6378875.

Абсолютная погрешность аргумента е_у = 0,005. Тогда абсолютные и относительные погрешности величины у равны:

е_у = 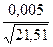= 1,078077 ∙ 10^-3;

δ_у = 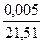= 2,3245002 ∙ 10^-4 < 0.5 ∙ 10^-3;

Это означает, что в числе 4,6378845 три цифры после запятой верны в строгом смысле.

Ответ: 4,6378.

г) Находим значение величины у. Оно будет равно 4,2226498.

Абсолютная погрешность аргумента е_у = 0,0005. Тогда абсолютные и относительные погрешности величины у равны:

е_у = 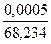= 7,3298736 ∙ 10^-6;

δ_у = 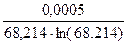= 1,7358469 ∙ 10^-6 < 0,5 ∙ 10^-5.

Это означает, что в числе 4,2226498 пять цифр после запятой верны в строгом смысле.

Ответ: 4,222649.

Пример 1.15.

Вычислить значение величины с помощью метода строгого учета границ абсолютных погрешностей после каждой операции.

А = 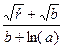, если а = 12,34, b = 14,3.

Решение.

При пооперационном строгом учете ошибок промежуточные результаты после округления до одной запасной (с учетом вычисленной параллельно величины погрешности) и их погрешности заносят в табл. 1.1.

Таблица 1.1. Расчетная таблица для вычисления

погрешности выражения А =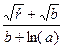

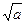
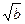
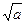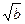а b + ln(a) b + ln(a) A

12,34 14.3 3.513 3.78 7.30 2.5129 16.81 0.434

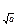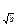e_a e_b e e 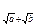e e 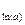e_{b + ln(a)} e_A

0.005 0.05 0.00071 0.0066 0.0073 0.0004 0.05041 0.0017

Значения погрешностей для удобства округлим до двух значащих цифр по избытку и тоже занесем в таблицу.

Цифры даны верными в строгом смысле, значит, е_а = 0,005, е_b = 0,05.

Найдем 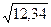= 3,51283. Абсолютная погрешность равна (воспользуемся табл. 1.1):

е_а = 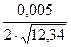= 0,0007117 ≈ 0,00071.

Из полученного значения погрешности видно, что в результате верны две значащие цифры после запятой, т. е.

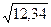= 3,51283 ≈ 3,513.

Это число внесем в таблицу.

Найдем абсолютную погрешность 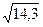= 3,781534.

Она будет равна е_b = 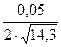= 0,0066107 ≈ 0,0066.

Значит, в числе b будет одна верная цифра после запятой.

Аналогично находим значения всех остальных действий и функций:

е 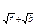= 0,00071 + 0,0066 = 0,00731 ≈ 0,0073;

е_ln(а) = 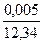= 0,000405 ≤ 0,0005;

е_{b + ln(a)} = 0.05 + 0.000405 = 0.050405 ≤ 0.5;

е_А = 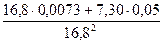= = 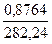0,0017.

Округляя результат А до верной цифры, получаем окончательный ответ.

Ответ: А = 0,434 ± 0,002.

Способ границ

Способ границ используется для точного определения границ искомого значения функции, если известны границы измерения ее аргументов.

Пример 1.16.

Алюминиевый цилиндр с диаметром основания d = (3 ± 0,001) см и высотой h = (10 ± 0,002) см весит p = (95,5 ± 0,001) г. Определить удельный вес γ алюминия и оценить предельную абсолютную погрешность найденного удельного веса.

Решение.

1 способ.

Объем цилиндра равен:

V = 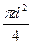h,

отсюда

γ = .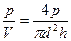

Из полученной формулы вытекает, что в области p > 0, d > 0, h > 0 функция γ – возрастающая по аргументу p и убывающая по аргументам d и h.

Имеем:

2,999 < d < 3,001;

9,998 < h < 10,002;

95,499 < p < 95,501;

3,14159 < π < 3,1416.

Тогда для значения γ получим:

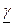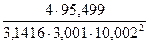= = 1,350 г/см³ (нижняя граница);

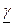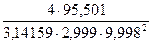= = 1,352 г/см³ (верхняя граница).

Взяв среднее арифметическое, получим значение γ, равное

γ = (1,351 ± 0,002) г/см³.

Ответ: γ = (1,351 ± 0,002) г/см³.

2 способ.

Используя средние значения аргументов, получим

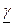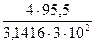= = 1,351 г/см³.

Логарифмируя формулу для вычисления объема цилиндра, имеем

ln γ = ln 4 + ln p – ln π – 2 ln d – ln h.

Взяв полный дифференциал, получим:

;

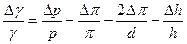δ_γ = δ_p + δ_π + 2δ_d + δ_h = 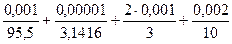= 8.803 ∙ 10^-4

Далее находим:

Δ_γ = δ_γ ∙ γ = 8,803 ∙ 10^-4 ∙ 1,351 = 1,2 ∙ 10^-3.

Таким образом, имеем:

γ = (1,351 ± 0,001) г/см³,

что очень близко совпадает с точной оценкой, найденной по способу границ.

Ответ: γ = (1,351 ± 0,001) г/см³.

Пример 1.17.

Найти предельные абсолютную и относительную погрешности вычисления объема шара по выражению V = 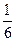πd³, если d = 3,7 ± 0,05 см, а π = 3,14.

Решение.

Рассматривая d и π как переменные величины, вычисляем частные производные

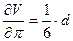³ = 8,44;

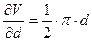² = 21,5.

Используя формулу для вычисления погрешности функции, зависящей от двух переменных

│Δf│ = ,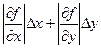

находим предельную абсолютную погрешность объема

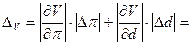8,44 ∙ 0,0016 + 21,5 ∙ 0,05 = 0,013 + 1,075 = 1,088 см³ ≈ 1,1 см³.

Поэтому

V = 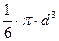≈ (26.5 ± 1.1) см³.

Отсюда предельная относительная погрешность определения объема

δ_V = 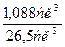= 0,041 ≈ 4%.

Ответ: ΔV = 1,1 см³, δ_V = 4%.

Пример 1.18.

Для определения модуля Юнга Е по прогибу стержня прямоугольного сечения применяется формула Е = 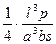, где l – длина стержня; a и b – измерения поперечного сечения стержня; s – стрела прогиба; p – нагрузка. Вычислить предельную относительную погрешность при определении модуля Юнга Е, если p = 20 кг; δ_p = 0,1%; а = 3 мм; δ_а = 1%; b = 44 мм; δ_b = 1%; l = 50 см; δ_l = 1%; s = 2,5 см; δ_s = 1%.

Решение.

Ln E = 3ln l + ln p – 3ln a – ln b – ln s – ln 4.

Отсюда, заменяя приращения дифференциалами, будем иметь:

.

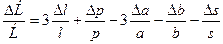Следовательно,

δ_Е = 3δ_l + δ_p + 3 δ_а + δ_b + δ_s = 3 ∙ 0,01 + 0,001 + 3 ∙ 0,01 + 0,01 + 0,01 ≈0,081. Таким образом, относительная погрешность составит не более 0,081, т. е. примерно 8% от измеряемой величины.

Ответ: δ_Е ≈ 8%.

Пример 1.19.

Вычислить значение величины z с помощью Mathcad при заданных значениях а, b и c с систематическим учетом абсолютных погрешностей после каждой операции, если цифры верны в строгом смысле.

z = 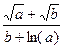, a:= 12,34 b:= 14,3.

Решение.

Алгоритм решения представлен на рис. 1.3 – 1.5

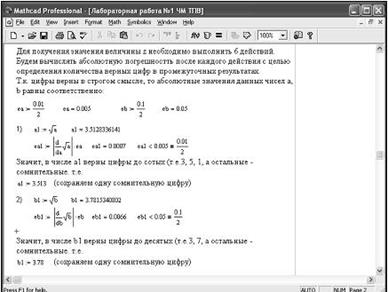
Рис. 1.3.Первый этап решения задачи примера 1.19

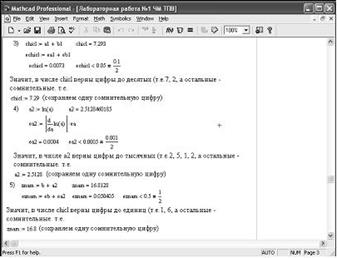
Рис. 1.4. Второй этап решения задачи примера 1.19

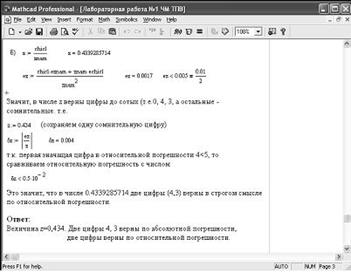
Рис. 1.5. Третий этап решения задачи примера 1.19