Метод простой итерации
Пример 2.3.
Решить уравнение 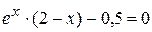 методом простой итерации с точностью ɛ = 0,001.
методом простой итерации с точностью ɛ = 0,001.
Решение.
Схема решения уравнения методом простой итерации следующая.
1. Отделяем корни.
2. Приводим исходное уравнение к виду х = f(х).
Заменим уравнение 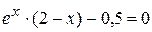 уравнением вида
уравнением вида 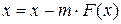 .
.
Здесь величина m должна быть подобрана так, чтобы для функции f(x) выполнились условия 2 и 3 теоремы о достаточном условии сходимости итерационного процесса.
Производная Fˈ(х) на отрезке [1,5; 2,5] отрицательна, следовательно, функция F(х) на этом отрезке монотонно убывает. Ее значения представлены на рис. 2.7.
| 1,7408 |
| 1,4812 |
| 1,1422 |
| 0,7099 |
| 0,1686 |
| -0,5 |
| -1,3166 |
| -2,305 |
| -3,4923 |
| -4,9093 |
| -6,5912 |
F(х) =
Рис. 2.7.Значение функции 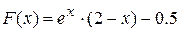
на отрезке [1,5; 2,5]
Тогда значения функции f(x) будут равны:
f(1.5) = 1,5 – m∙1,741;
f(2,5) = 2,5 – m∙(-6,591).
Учитывая монотонность функции f(x), из последних равенств легко заметить, что условие 2 указанной теоремы будем заведомо выполнено, если m – правильная отрицательная дробь (рис. 2.8).
x = 1,5; 1,6…2,5 F(x) = (2 – x)∙ex – 0,5
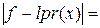
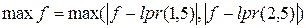

Рис.2.8.Определение значения m
Поскольку производная Fˈ(x) на концах интервала [1,5; 2,5] положительна (Fˈ(1,5) = 2,241, Fˈ(2,5) = 18,274) и монотонно возрастает, ее модуль имеет максимум на правом конце отрезка. Тогда если за m принять число 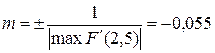 , то для любого х из отрезка [1,5; 2,5] значение выражения будет правильной отрицательной дробью. Это обеспечивает выполнение условия 2 теоремы (рис.2.9.).
, то для любого х из отрезка [1,5; 2,5] значение выражения будет правильной отрицательной дробью. Это обеспечивает выполнение условия 2 теоремы (рис.2.9.).
Для выполнения условия 3 указанной выше теоремы 2.2 найдем производную преобразованной функции
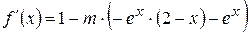
и ее значения на концах отрезка [1,5; 2,5].
Условие 3 теоремы выполнено: значения производных меньше единицы. За величину q возьмем число 0,877 (рис. 2.9.).
f(x) = x – mF(x)
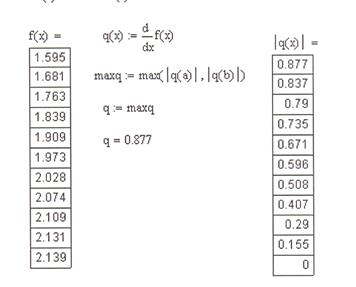
Рис. 2.9.Определение значения q
3. Вычисляем значения итерационной последовательности 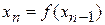 .
.
В качестве начального значения возьмем, например, начало отрезка, точку х0 = 1,5.
Критерием достижения заданной точки ɛ = 0,001 при решении нашего уравнения методом простой итерации является величина, равная 1,398∙10-5 (рис. 2.10).
q = 0,877
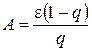
A = 1.398∙10-5
Рис. 2.10.Определение критерия достижения
заданной точности q
4. Строим итерационную последовательность (рис. 2.11).
i = 1..25 x0 = a z(x) = x – mf(x)
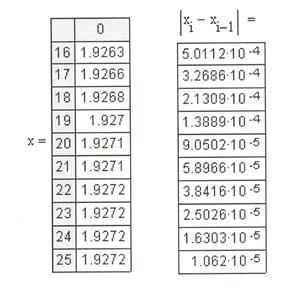 xi = z(xi-1)
xi = z(xi-1)
Рис. 2.11.Построение итерационной последовательности
по методу простой итерации
Для 24-го приближения получили, что 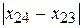 ˂ 1,398∙ 10-5 ˂А. Отсюда следует, что х23 = 1,92718 является приближенным решением нашего уравнения.
˂ 1,398∙ 10-5 ˂А. Отсюда следует, что х23 = 1,92718 является приближенным решением нашего уравнения.
5. Создаем функцию, реализующую метод простой итерации, для решения уравнения x = f(x) по методу простой итерации (составляется аналогично рассмотренным выше методам).
6. Визуализируем решение уравнения методом простой итерации (рис. 2.12).
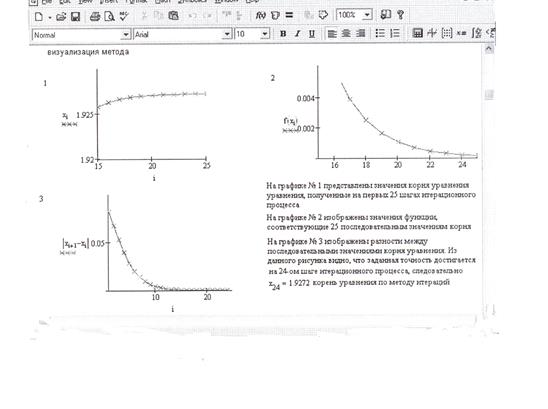
Рис. 2.12. Визуализация решения уравнения F(x) = (2 – x)∙ex – 0,5
Вопросы по теме
1. Что значит решить уравнение?
2. Каковы этапы решения уравнения с одной неизвестной численными методами?
3. Какие существуют методы решения с одной неизвестной?
4. В чем заключается этап отделения корней при использовании численных методов решения уравнения?
5. Суть метода хорд. Графическая интерпретация метода.
6. Суть метода касательных. Графическая интерпретация метода.
7. Суть метода простой итерации.
8. Какое уравнение можно решать методом простой итерации?
9. Каковы достаточные условия сходимости итерационного процесса при решении уравнения x = f(x) на отрезке [a, b], содержащего корень, методом простой итерации?
10. Какое условие является критерием достижения заданной точности при решении уравнения x = f(x) методом хорд, касательных, итерацией?
11. Записать формулу нахождения значений последовательности при решении уравнения методом: хорд, касательных.
12. Как строится итерационная последовательность точек при решении уравнения методом простой итерации?
Дата добавления: 2021-09-07; просмотров: 675;











