Аргумент комплексного числа.
Комплексные числа, которые имеют один и тот же модуль r, ІzІ= r, соответствуют точкам комплексной плоскости, которые расположены на окружности радиуса r, с центром в точке z=0. То есть, если r ≠0 , то существует множество комплексных чисел з данным модулем r. Модуль, который равен нулю, имеет только единственное комплексное число z=0.
Для того, чтобы с множества комплексных чисел с данным модулем выделить какое то конкретное число, достаточно задать направление вектора z (например, задать угол).
Аргументом комплексного числа z ≠0 называется угол, который образован положительным направлением действительной оси и вектором z. Причем угол считается положительным, если отсчет ведется против часовой стрелки и отрицательным, если отсчет идет по часовой стрелке.
Для обозначения аргумента комплексного числа z, используется запись arg z.
Заданием модуля и аргумента, комплексное число определяется однозначно.
Аргумент комплексного числа определяется неоднозначно. Любые два аргумента комплексного числа отличаются друг от друга числом кратным 2П.
Для вычисления аргумента комплексного числа: z=а+bi, используют формулы:
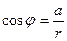 ;
; 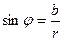 ;
; 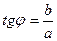 (6)
(6)
Для определения аргумента комплексного числа необходимо учитывать четверть (квадрант) в которой находится число.
Пример 1.
Найти аргумент чисел: 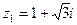 ;
; 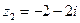
Решение:
Сначала найдем модули данных комплексных чисел (формула (2))
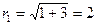 ;
; 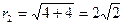 .
.
По формулам (6) найдем аргументы. Так как комплексное число 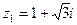 находится в І четверти, а число
находится в І четверти, а число 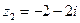 находится в ІІІ четверти, то углы будем определять соответственно четверти.
находится в ІІІ четверти, то углы будем определять соответственно четверти.
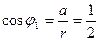 ; значит
; значит 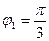 .
.
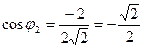 ,
, 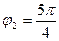 .
.
Дата добавления: 2020-06-09; просмотров: 860;











