В таких системах счисления от положения знака в записи числа не зависит величина, которую он обозначает; поэтому они называются непозиционными системами счисления.

Непозиционными системами пользовались древние египтяне, греки, римляне и некоторые другие народы древности.

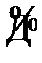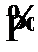На Руси вплоть до XVIII века, использовалась непозиционная система славянских цифр. Буквы кириллицы (славянского алфавита) имели цифровое значение, если над ними ставился специальный знак ~ титло. Например Ã — 1, — 4, — 100.

Непозиционные системы счисления были более или менее пригодны для выполнения сложения и вычитания, но совсем не удобны при умножении и делении.

Идея позиционной системы счисления впервые возникла в древнем Вавилоне.

В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции.

Количество используемых цифр называется основанием позиционной системы счисления.

Система счисления, применяемая в современной математике, является позиционной десятичной системой. Ее основание равно десяти, так как запись любых чисел производится с помощью десяти цифр:

0,1, 2, 3, 4, 5, 6, 7, 8, 9.

Хотя десятичную систему принято называть арабской, но зародилась она в Индии, в V веке. В Европе об этой системе узнали в XII веке из арабских научных трактатов, которые были переведены на латынь. Этим и объясняется название «арабские цифры». Однако широкое распространение в науке и в обиходе десятичная позиционная система получила только в XVIвеке. Эта система позволяет легко выполнять любые арифметические вычисления, записывать числа любой величины. Распространение арабской системы дало мощный толчок развитию мате­матики.

С позиционной десятичной системой счисления вы знакомы с раннего детства, только, возможно, не знали, что она так называется.

Позиционный тип этой системы легко понять на примере любого многозначного числа. Например, в числе 333 первая тройка означает три сотни, вторая — три десятка, третья — три единицы. Одна и та же цифра в зависимости от позиции в записи числа обозначает разные величины.

333 = 3x100 + 3x10 + 3.

Еще пример:

32478 = 3 х 10000 + 2 х 1000 + 4 х 100 + 7 х 10 + 8 =

= 3 х 10⁴ + 2 х 10³ + 4 х 10² + 7 х 10¹ + 8 х 10⁰.

Отсюда видно, что всякое десятичное число можно представить как сумму произведений составляющих его цифр на соответствующие степени десятки. То же самое относится и к десятичным дробям.

26,387 = 2 х 10¹ + 6 х 10⁰+ 3 х 10^-1 + 8 х 10^-2 + 7 х 10^-3