Интегральные критерии качества

Интегральными критериями (оценками) качества называются такие, которые одним числом (интегрально) оценивают качество переходного процесса в системе. Кроме того, такие оценки обычно являются интегральными функционалами и выражаются в следующем виде:

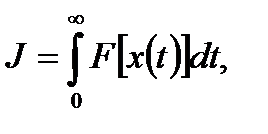
где F 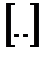– заданная функция, определяющая тип интегрального критерия; x(t) – отклонение переходной функции системы от значения h(∞), которое установится после окончания переходного процесса, т.е.

x(t) = h(∞) – h(t).(4.2)

Рис. 4.4. Графическое представление линейной интегральной оценки качества процесса регулирования: а – монотонного; б – колебательного

+

-

+

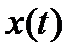
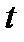
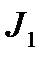
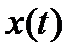
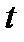
б)

а)

Как известно, качество переходного процесса в САУ оценивается совокупностью показателей. Зачастую при изменении параметров системы с целью обеспечения требуемых характеристик переходного процесса одни из показателей улучшаются, в то время как другие ухудшаются. В такой ситуации, когда задача выбора оптимальных значений параметров системы оказывается многокритериальной, а потому трудноразрешимой, использование интегральных критериев, оценивающих качество регулирования одним числом, оказывается предпочтительным.

Для монотонного процесса (рис. 4.4, а) интегральной оценкой может служить функционал следующего вида:

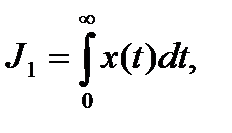
называемый линейной интегральной оценкой качества J₁. Ее численное значение равно площади под кривой переходного процесса. Очевидно, что динамика системы тем лучше, чем меньше значение J₁.

Для обеспечения требуемых динамических свойств САУ необходимо выразить величину J₁ через коэффициенты передаточной функции системы, а затем найти оптимальные значения варьируемых параметров, соответствующих минимуму J₁.

Поскольку

,

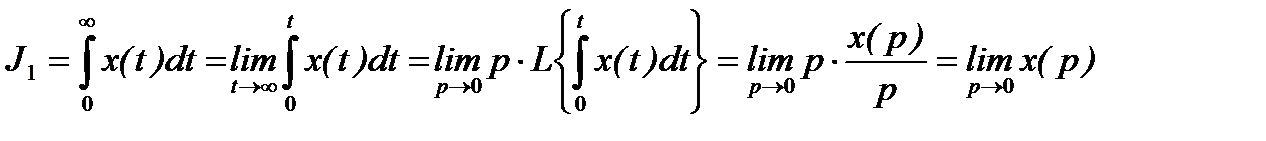и учитывая, что

= ,

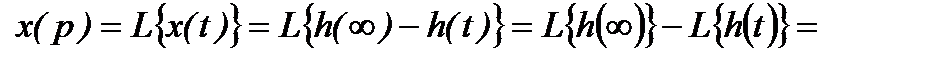
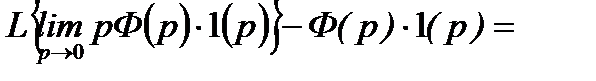
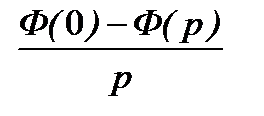(где 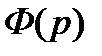- передаточная функция замкнутой системы), получаем выражение для расчета величины линейной интегральной оценкой качества J₁ по передаточной функции системы:

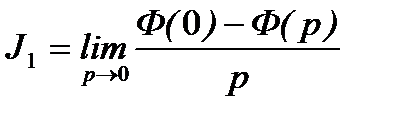. (4.3)

Так, например, для системы с передаточной функцией

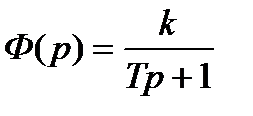
интегральная оценка J₁ , согласно выражению (4.3), равна:

.

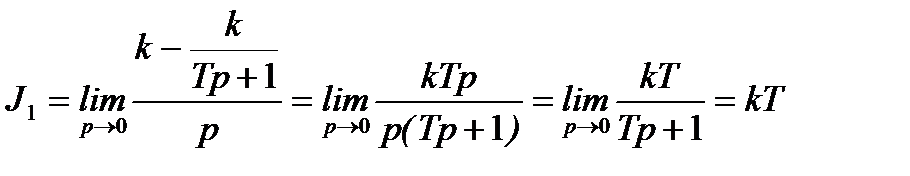Для системы с передаточной функцией

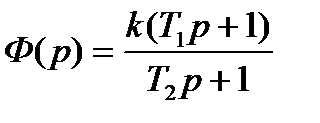
интегральная оценка

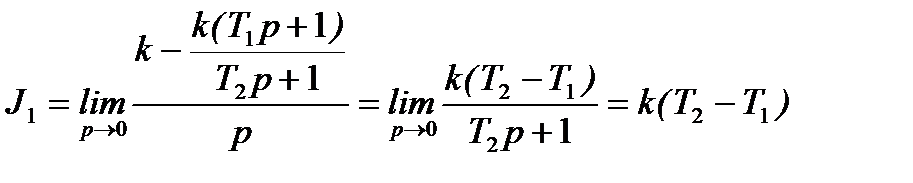
зависит от соотношения постоянных времени 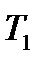и .

И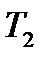спользование линейной интегральной оценки J₁ возможно только для монотонных процессов и неприемлемо для оценки качества колебательных систем. Для колебательных процессов величина критерия, равная разности между суммой положительных и отрицательных площадей (см. рис. 4.4, б), не будет однозначно связана с действительным качеством регулирования системы.

Например, ухудшение качества переходного процесса при переходе к незатухающим колебаниям будет сопровождаться уменьшение критерия J₁ до нуля. В связи с этим при наличии перерегулирования в переходном процессе и колебательном его характере применяют квадратичную интегральную оценку качества J₂ следующего вида:

.

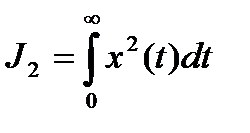Величина квадратичной интегральной оценки J₂ равна площади, ограниченной кривой x²(t) (рис. 4.5, а).

В справочной литературе приведены формулы, выражающие величину критерия J₂ непосредственно через коэффициенты дифференциального уравнения замкнутой системы.

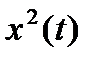
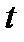
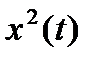
t

а)

Рис. 4.5. Графическое представление квадратичной интегральной оценки качества процесса регулирования

б)

Данный критерий является наиболее широко используемым интегральным критерием качества, однако в ряде случаев он также не дает достоверной оценки характера переходного процесса. На рис. 4.5, б приведены графики x²(t) для монотонного процесса (кривая 1) и колебательного процесса (кривая 2). Очевидно, что значение критерия J₂ для колебательного процесса будет меньше, в то время как более предпочтительным является монотонный процесс: ему соответствует плавное изменение выходного сигналы и отсутствие значительных динамических воздействий в системе.

Недостатки рассмотренных интегральных оценок качества обусловили использование обобщенного (улучшенного) интегрального критерия, имеющего в простейшем случае следующий вид:

.

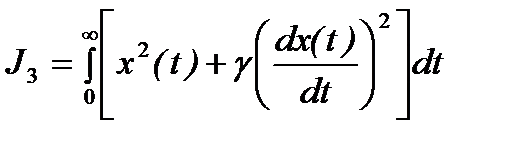Использование интегральной оценки J₃ позволяет обеспечить в системе быстро затухающий, но достаточно плавный процесс, поскольку наличие в подынтегральном выражении слагаемого 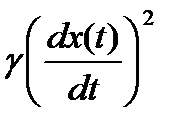ограничивает скорость изменения регулируемой величины, снижая колебательность системы.Чем больше коэффициент 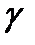, тем значительнее влияние указанного слагаемого, тем более плавным будет переходный процесс, но зато и более длительным.

В качестве интегральных критериев используются и функционалы более общего вида. Иногда в выражении интегральной оценки вводится время t в явном виде.

Наиболее широко интегральные критерии применяются в теории оптимальных систем автоматического управления.

Вопросы для самопроверки

1. Назовите основные показатели качества процесса регулирования, определяемые по переходной функции системы.

2. Как по виду переходной функции системы определяется время регулирования?

3. Что характеризует величина перерегулирования?

4. Что называется нормированной амплитудно-частотной характеристикой системы?

5. Как связана ширина полосы пропускания системы с ее быстродействием?

6. Укажите диапазон изменения значений показателя колебательности, для которых качество регулирования считается удовлетворительным?

7. Какими критериями оценивается качество переходных процессов в зависимости от расположения полюсов передаточной функции замкнутой системы?

8. К каким системам при оценке качества их переходных процессов можно применять линейную интегральную оценку?