Основные положения метода переменных состояния

Рассмотрим основные положения ме­тода переменных состояния и его применение для анализа САУ. С математической точки зрения это предполагает ис­пользование методов матричного исчисления и векторного анализа. Подход, основанный на поня­тии переменных состояния системы, особенно удобен для описания многосвязных или нестационарных линейных систем, а также нелинейных систем, исследование которых с помощью методов, базирующихся на использовании передаточных функций и частотных характеристик САУ, часто бывает затруднительным. Использование математического аппарата теории матриц и матрич­ных уравнений позволяет получить основные зависимости в компактном виде, удобном для исследования систем на ЦВМ.

Основное положение метода переменных состояния заключается в следующем. Для полного математического описания динамической системы 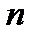-го порядка необходимо ввести в рассмотрение 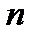независимых переменных состояния системы 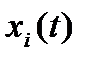. Эти переменные должны быть выбраны так, чтобы, зная начальное состояние системы 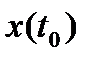в момент t = t₀,можно было бы при известных на интервале t₀ ≤ t ≤ t₁входных воздействиях 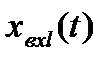, определить состояние 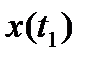в момент времени .

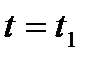При описании системы в пространстве состояния целесообраз­но разделить все сигналы, характеризующие поведение системы, на три группы:

1) входные сигналы или входные воздействия 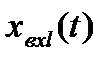, приложенные к исследуемой системе со стороны других систем, ;

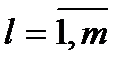2) выходные сигналы 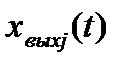, характеризующие реакцию системы на указанные входные воздействия, ;

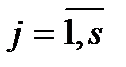3) промежуточные переменные 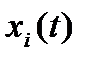, характеризующие внутреннее состояние системы, .

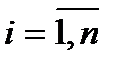Для удобства описания каждую группу переменных можно представить в виде вектора (матрицы-столбца):

X_вх(t) = 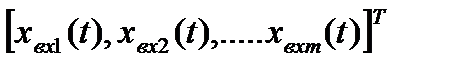– вектор входных воздействий;

X_вых(t)= 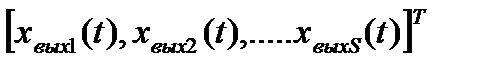– вектор выходных переменных системы;

X(t) = 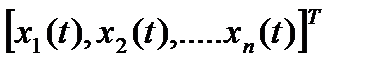– вектор переменных состояния системы.

Приведенная классификация сигналов в системе является в определенной степени условной, так, некоторые переменные состояния 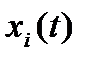могут совпадать с выходными сигналами 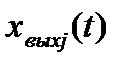, но в общем случае между ними существует следующая зависимость:

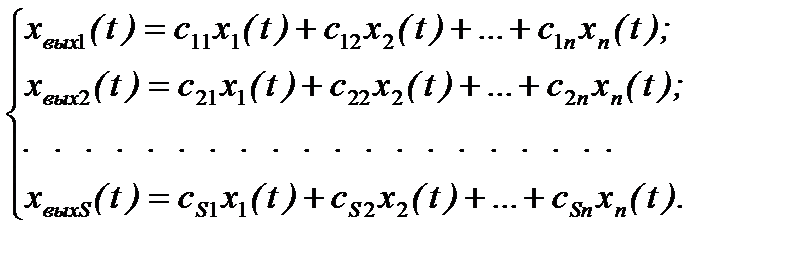(6.1)

В пространстве состояния,осями координат которого являются переменные состояния, каждому моменту времени соответствует вектор X(t). Величина и положение этого вектора с течением времени изменяются, в результате чего конец вектора X(t) описывает кривую, называемую траекторией движения системы в пространстве состояний.

Динамика линейной стационарной САУ 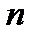-го порядка может быть описана системой 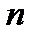линейных дифференциальных уравнений:

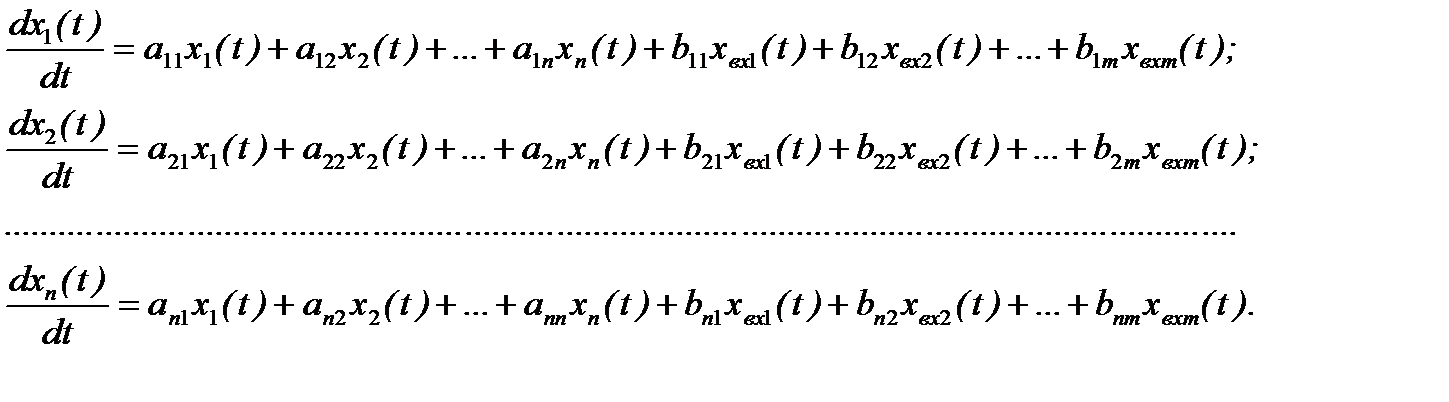(6.2)

Систему уравнений (6.2) можно записать в виде сле­дующего матричного (векторного) дифференциального уравнения:

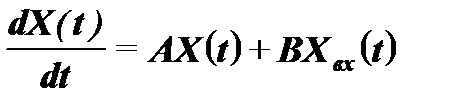, (6.3)

где А 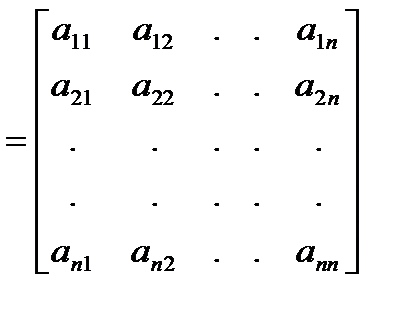– матрица системы (квадратная матрица размером );

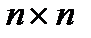B 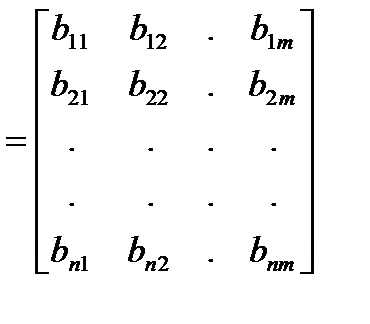– матрица управленияразмером .

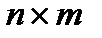В матричной форме система уравнений (6.1) примет вид:

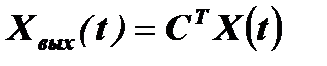, (6.4)

где С 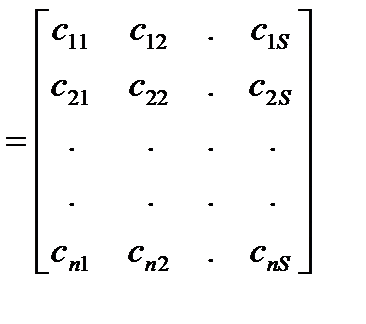– матрица наблюдения размером .

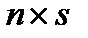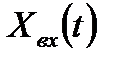
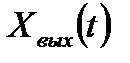
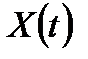
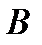
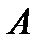
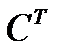
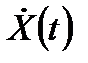
Рис. 6.1. Структурная схема САУ в векторной форме

Уравнения (6.3) и (6.4) называют уравнениями состояния системы.

Элементы матрицы системы Аопределяются структур­ной схемой системы и значениями ее параметров. Матри­ца управления В характеризует влияние входных сигналов на переменные состояния, а матрица наблюдения С определяет связь выходных сигналов системы с вектором состояния. Обычно не все составляющие вектора состояния являются наблюдаемыми сигналами, т. е. они не могут быть измере­ны с помощью каких-либо датчиков, в то время как вы­ходные сигналы всегда наблюдаемы.

На рис. 6.1 показана структурная схема системы, соответствующая векторным урав­нениям (6.3) и (6.4); двойные линии на рисунке характеризуют векторный характер сигналов.

Согласно определению понятия состояния системы, в любой момент времени
t > t₀ состояние системы является функцией начального состояния X(t₀) и вектора входа X_вх(t₀ , t), т.е.

X(t) = F[X(t₀),X_вх(t₀ , t)]. (6.5)

Вектор выхода в момент t также однозначно связан с векторами X(t₀) и X_вх(t₀ , t):

X_вых(t) = R[X(t₀),X_вх(t₀ , t)]. (6.6)

Приведенные векторные дифференциальные уравнения описывают линейные стационарные САУ. В нестационар­ных системах элементы матрицы в уравнениях (6.3) и (6.4) являются функциями времени, и векторные дифференциальные уравнения принимают вид:

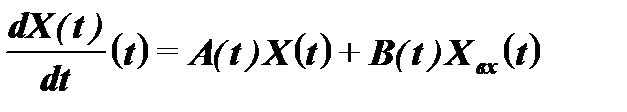; (6.7)

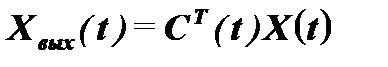. (6.8)