Алгоритм расчета структуры изображения с использованием функции размытия линии.

Функция размытия линии может быть нормирована так, что:

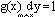
или сам интеграл:

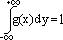
Расчет:

Если мы имеем распределение яркости производного объекта

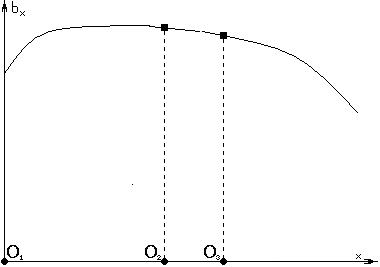
Наш объект проходит через систему.

ФРЛ g(u)

Рассмотрим распределение в точке 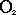. Эта точка 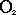имеет координату x. После прохождения системы, эта точка будет иметь другую интенсивность. Для того, чтобы знать, что у нас происходит в точке 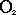, рассмотрим точку .

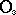Интенсивность в точке 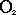будет зависеть от в том числе и от точки 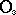- та будет давать свой “вклад” пропорционально g(u)du.

В целом, интенсивность точки 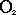будет формироваться , в зависимости от точки 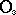по виду: b(x-u)g(u)du.

В точке 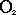интенсивность, которая будет формироваться от щели, светящейся в точке 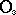будет пропорциональна интенсивности объекта точки 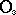, то есть, b(x-u), пропорционально значению функции g(u) в точке 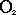, если вершина этой точки в точке .

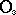В целом же интенсивность, формирующаяся в точке 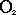будет соответствовать сумме вкладов всех остальных точек b(x).

В целом, интенсивность от всех точек будет равно интегралу:

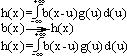
Операция интегрирования называется операцией свертки, а интеграл называется интегралом свертки.

Операция и интеграл свертки позволяют нам, зная функцию размытия системы, найти распределение интенсивности уже на выходе информационной системы вследствие фильтрации.

Операция свертки справедлива только для линейных систем.

Функция ФРТ и ФРЛ позволяют однозначно рассчитывать любой сигнал.

Краевая функция

Край полуплоскости – это резкая, прямолинейная граница между освященной и неосвященной частями пространства. Этот край можно определить как скачкообразную функцию. Математическое описание края можно описать так:

В яркой части полуплоскости B(x)=1

В темной части полуплоскости B(x)=0.

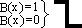
В инерционной системе будет плавно перераспределен скачок как размытие.

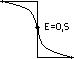
Краевая функция будет плавная, симметричная, при чем срединное значение будет равно 0,5. Е=0,5.

Используя интеграл свертки 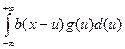, и подставляя в него значение интенсивности края полуплоскости b=1, получим:

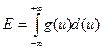
И наоборот – из краевой функции можно дифференцированием получить краевую функцию.