Численное интегрирование.

Задача численного интегрирования состоит в замене исходной подинтегральной функции f(x), для которой трудно или невозможно записать первообразную в аналитике, некоторой аппроксимирующей функцией φ(x). Такой функцией обычно является полином (кусочный полином) 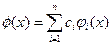. То есть:

,

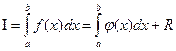где 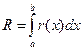– априорная погрешность метода на интервале интегрирования,

а r(x) – априорная погрешность метода на отдельном шаге интегрирования.

Обзор методов интегрирования.

Методы вычисления однократных интегралов называются квадратурными (для кратных интегралов – кубатурными).

1) Методы Ньютона-Котеса. Здесь φ(x) – полином различных степеней. Сюда относятся метод прямоугольников, трапеций, Симпсона.

2) Методы статистических испытаний (методы Монте-Карло). Здесь узлы сетки для квадратурного или кубатурного интегрирования выбираются с помощью датчика случайных чисел, ответ носит вероятностный характер. В основном применяются для вычисления кратных интегралов.

3) Сплайновые методы. Здесь φ(x) – кусочный полином с условиями связи между отдельными полиномами посредством системы коэффициентов.

4) Методы наивысшей алгебраической точности. Обеспечивают оптимальную расстановку узлов сетки интегрирования и выбор весовых коэффициентов ρ(x) в задаче 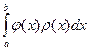. Сюда относится метод Гаусса-Кристоффеля (вычисление несобственных интегралов) и метод Маркова.