Оценка апостериорной погрешности.

Мы записывали априорные оценки главного члена погрешности в виде R₀ = Ah^p, (1) где A – коэффициент, зависящий от метода интегрирования и вида подинтегральной функции; h – шаг интегрирования, p – порядок метода. Такого сорта оценку можно применить не только к методам интегрирования, но и ко многим другим численным алгоритмам.

Первая формула Рунге.

Пусть w – точное значение, к которому должен прийти численный метод (мы его не знаем). Результат численного расчета дает нам величину w_h такую, что 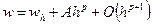. (2)

Теперь вычислим ту же величину w с шагом kh, где константа k может быть как больше, так и меньше единицы. Коэффициент A будет одинаковый, так как вычисление осуществляется одним и тем же методом. Получаем 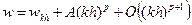. (3)

Приравняем правые части выражений (2) и (3) и пренебрежем бесконечно малыми величинами одинакового порядка малости.

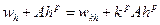. Отсюда, учитывая (1), получим 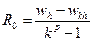. (4) Эта формула, выражающая апостериорную оценку главного члена погрешности величины w путем двойного просчета с разным шагом, носит название первой формулы Рунге. При уменьшении шага главный член погрешности будет стремиться к полной погрешности R.