Примеры практического использования принципа суперпозиции для расчёта распределения потенциала электростатического поля в пространстве.

В разделе 2.4.8 рассмотрен принцип суперпозиции для потенциала электростатического поля и приведены зависимости (3) - (5) для расчёта потенциала электростатического поля для случаев, когда электростатическое поле образовано дискретными электрическими зарядами или зарядами, распределёнными по объёму, или по поверхности, или по пространственной кривой:

, , .

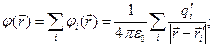
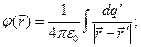
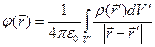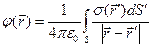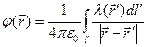В рассматриваемых зависимостях должны быть a priori известны распределения электрических зарядов в пространстве, т.е. величины сосредоточенных зарядов и их расположение в пространстве или плотности распределения и геометрия области, занятой зарядами. В некоторых случаях эта информация может быть получена из физических представлений. В общем случае проблема определения распределения электрических зарядов, в частности, по поверхности проводника, является самостоятельной задачей.

Ниже рассмотрим несколько примеров расчёта распределения потенциала электростатического поля в пространстве, когда поле образовано электрическими зарядами с известной плотностью распределения.

2.4.11.1. Поле равномерно заряженного плоского диска.

Пусть тонкий диск радиуса а расположен в плоскости z=0 декартовой системы координат, причем его центр симметрии совпадает с началом системы координат, а поверхностная плотность электрического заряда 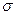является постоянной величиной (рис.1). Координаты точки наблюдения М обозначим через x ,y и z. Координаты точки расположения элементарного электрического заряда, формирующего электрическое поле, опишем соотношениями:

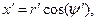
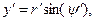
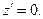(1)

Здесь величина 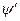является естественной угловой координатой, а 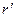- естественной радиальной координатой точки в цилиндрической системе координат, оси которой

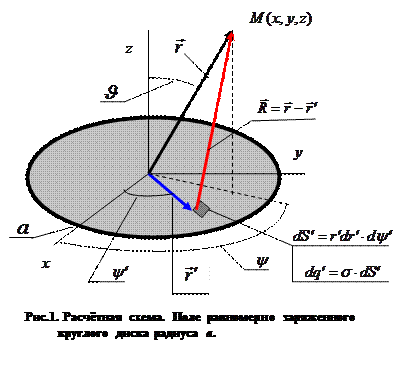
согласованы с исходной декартовой системой координат. Расстояние между точкой расположения элементарного заряда и точкой наблюдения имеет вид:

,

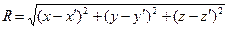что эквивалентно

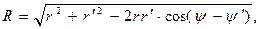
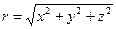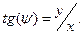, (2)

Дифференциал потенциала электрического поля запишем в форме:

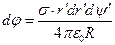. (3)

В силу осевой симметрии распределения электрического заряда достаточно рассмотреть случай y=0 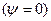. В этом случае интегрирование выражения (3) по угловой координате в пределах от 0 до 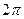приводит к соотношению

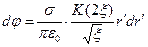, (4)

где 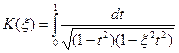- табулированный полный эллиптический интеграл первого рода, 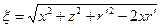. Подобные выражения встречались в разделе 2.2 настоящего учебного пособия. Далее формально можно записать выражение, получающееся после интегрирования (4) по радиальной координате 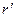в пределах от нуля до величины а, но конкретные результаты можно получить только численно для фиксированных значений x и z. Ниже рассмотрим точки наблюдения, лежащие на оси симметрии задачи (т.е. при x=0), что позволит получить замкнутые аналитические зависимости. Выражение (4) трансформируется при этом к виду:

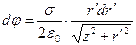, (5)

а вычисление интеграла даёт выражение

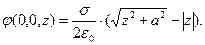(6)

Формула (6) позволяет рассчитать проекцию напряженности электростатического поля на ось аппликат:

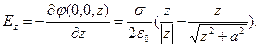(7)

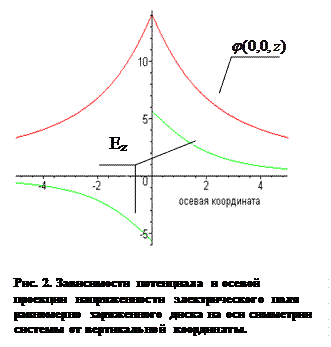Характерные графики зависимостей (6) и (7) приведены на рис.2, расчёты выполнены для следующих значений физических величин: а=2,5 м.,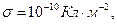 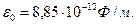Интересно отметить, что распределение потенциала электростатического поля равномерно заряженного диска вдоль оси симметрии системы непрерывно при переходе через поверхность диска z=0

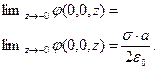(8)

Для распределения проекции напряженности электрического поля на ось аппликат получаем:

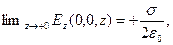
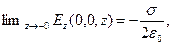
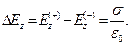(9)

Величина скачка нормальной к заряженной поверхности компоненты напряженности электростатического поля, умноженного на величину электрической постоянной равна поверхностной плотности электрического заряда. С этим результатом мы уже встречались в разделе 2.2.

2.4.11.2.Поле равномерно заряженной сферы.

Рассмотрим поверхность сферы радиуса а, центр которой совпадает с началом декартовой и сферической систем координат, естественно согласованных между собой. Пусть электрический заряд сферы распределен по поверхности сферы с постоянной поверхностной плотностью электрического заряда 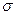. Элемент поверхности сферы 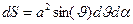несет на себе электрический заряд 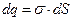. Сферические координаты точки расположения элементарного электрического заряда суть ( 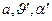), сферические координаты точки наблюдения обозначим ( 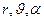). Соответствующие декартовы координаты имеют вид:

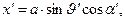
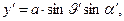
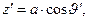(1)

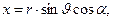
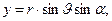
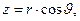(2)

что даёт возможность вычислить расстояние между рассматриваемыми точками:

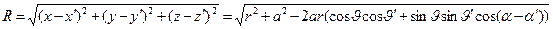. (3)

Запишем выражение для дифференциала потенциала в точке наблюдения:

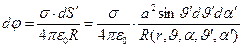. (4)

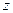Выражение для потенциала можно получить формальным интегрированием соотношения (4) по поверхности сферы. Но если воспользоваться свойством сферической симметрии системы распределения электрических зарядов, можно положить , т.е. направить ось из начала координат в точку наблюдения. Выражение (4) при этом принимает простую форму, и интегрирование выполняется в аналитическом виде:

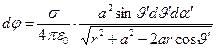, (5)

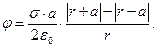(6)

Выражение (6) при r=a принимает значение

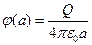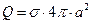, , (7)

где Q – суммарный электрический заряд сферы. При r>a зависимость потенциала от радиальной координаты аналогична зависимости потенциала поля от точечного заряда, расположенного в начале координат:

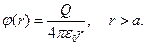(8)

При r<a из результата (6) следует

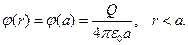(9)

Итак, прямым вычислением мы показали, что при равномерном распределении электрического заряда по поверхности сферы потенциал внутри сферы является постоянной величиной и обладает свойством непрерывности при переходе через заряженную поверхность.

Зависимость (6) позволяет вычислить радиальную составляющую напряженности рассматриваемого электростатического поля:

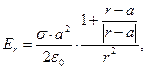(10)

что эквивалентно формулам:

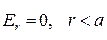, (11)

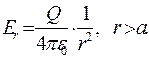(12)

Заметим, что и в рассматриваемом случае разность значений напряженности электростатического поля вне сферы и внутри сферы при r=a равна поверхностной плотности электрического заряда на поверхности сферы, деленной на электрическую постоянную .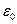

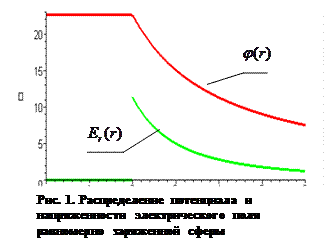
Зависимости для потенциала (формула 6) и радиальной составляющей напряженности электрического поля (формула 10) приведены на рис.1. Расчеты выполнены для следующих значений физических величин:

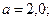
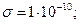
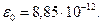Размерности физических величин соответствуют системе СИ.

В заключение раздела заметим, что полученные результаты поучительно сравнить с результатами раздела 2.2.