Энергия взаимодействия точечных электрических зарядов в вакууме.
Рассмотрим взаимодействие двух точечных электрических зарядов 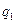 и
и 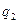 , положение которых в однородном пространстве с относительной диэлектрической проницаемостью
, положение которых в однородном пространстве с относительной диэлектрической проницаемостью 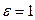 (т.е. среда - вакуум) определено радиус-векторами
(т.е. среда - вакуум) определено радиус-векторами 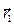 и
и 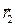 соответственно. Выражение для силы, с которой первый из зарядов действует на второй заряд, имеет вид:
соответственно. Выражение для силы, с которой первый из зарядов действует на второй заряд, имеет вид:
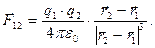 (1)
(1)
Аналогичное выражение имеет место и для силы, с которой второй заряд действует на первый:
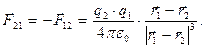 (2)
(2)
Допустим, что рассматриваемые заряды бесконечно медленно сместились из своего первоначального положения на бесконечно малые приращения радиусов-векторов 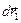 и
и 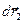 соответственно. Вычислим работу, совершаемую силами (1) и (2) на указанных перемещениях:
соответственно. Вычислим работу, совершаемую силами (1) и (2) на указанных перемещениях:
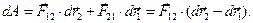 (3)
(3)
Если ввести обозначения 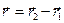 ,
, 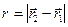 ,
, 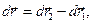
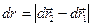 , можно получить следующее соотношение:
, можно получить следующее соотношение: 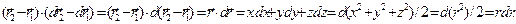 (4)
(4)
С учётом полученного соотношения выражение для элементарной работы dA принимает вид:
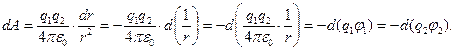 (5)
(5)
В этом выражении величина 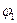 представляет собой потенциал электростатического поля в точке расположения первого заряда, образованного вторым зарядом (поле первого заряда исключено из рассмотрения!), аналогичный физический смысл имеет и величина
представляет собой потенциал электростатического поля в точке расположения первого заряда, образованного вторым зарядом (поле первого заряда исключено из рассмотрения!), аналогичный физический смысл имеет и величина 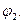 Если в понятие «энергия электростатического поля» не включать энергию образования электрических зарядов (т.е. не рассматривать сингулярное «собственное» поле зарядов), в силу потенциальности кулоновского взаимодействия можно записать выражение для дифференциала энергии взаимодействия электрических зарядов (или условно - энергии электростатического поля)
Если в понятие «энергия электростатического поля» не включать энергию образования электрических зарядов (т.е. не рассматривать сингулярное «собственное» поле зарядов), в силу потенциальности кулоновского взаимодействия можно записать выражение для дифференциала энергии взаимодействия электрических зарядов (или условно - энергии электростатического поля)
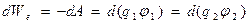 (6)
(6)
и после соответствующего выбора произвольной постоянной получить для энергии взаимодействия электрических зарядов выражение, учитывающее «равноправие» электрических зарядов в системе (симметричная форма записи):
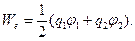 (7)
(7)
Заметим, что в рамках электростатики не имеет смысла вопрос, чему приписать электрическую энергию, полю или зарядам, поскольку не существует эксперимент, позволяющий однозначно решить эту задачу.
Результат (7), справедливый для случая двух зарядов в системе, можно обобщить на случай системы с произвольным числом точечных электрических зарядов:
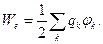 (8)
(8)
Обобщение (8) выглядит очень правдоподобно и естественно, но поскольку ему придаётся большое значение, полезно доказать его справедливость. Сделаем это методом полной математической индукции. Для случая двух зарядов в системе оно справедливо. Считаем, что оно справедливо и для случая n-1 электрических зарядов. Последнее означает, что имеет место соотношение:
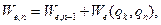 (9)
(9)
где первое слагаемое правой части описывает энергию системы n-1 зарядов, а второе слагаемое описывает энергию взаимодействия каждого из n-1 зарядов с оставшимся зарядом (с индексом n) рассматриваемой системы. В силу сделанных предположений запишем:
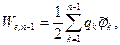 (10)
(10)
где волна над символом потенциала 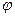 означает, что он вычисляется без учета поля заряда с индексом n. Для второго слагаемого правой части формулы (9) имеем:
означает, что он вычисляется без учета поля заряда с индексом n. Для второго слагаемого правой части формулы (9) имеем:
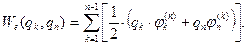 (11)
(11)
Здесь символ 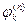 обозначает потенциал поля, образованного зарядом с индексом n, в точке расположения заряда с индексом k, а символ
обозначает потенциал поля, образованного зарядом с индексом n, в точке расположения заряда с индексом k, а символ 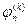 - потенциал поля, образованного зарядом с индексом k, в точке расположения заряда с индексом n. При объединении выражений (10) и (11) очевидно, что
- потенциал поля, образованного зарядом с индексом k, в точке расположения заряда с индексом n. При объединении выражений (10) и (11) очевидно, что
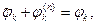
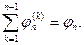 (12)
(12)
Последнее позволяет записать результат
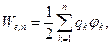 (13)
(13)
что завершает доказательство.
2.4.10.Энергия системы распределённых по объёму электрических зарядов в вакууме.
Обобщение соотношения (8) предыдущего раздела на случай системы с распределёнными по объёму тела электрическими зарядами часто записывают в виде:
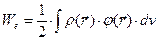 , (1)
, (1)
где 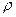 - объёмная плотность электрических зарядов, при этом в отдельных учебниках констатируют «идентичность» выражения (13) предыдущего раздела и выражения (1), в других этот вопрос не затрагивается, в третьих подчеркивается разница физического содержания обсуждаемых выражений. Поскольку элементарный электрический заряд
- объёмная плотность электрических зарядов, при этом в отдельных учебниках констатируют «идентичность» выражения (13) предыдущего раздела и выражения (1), в других этот вопрос не затрагивается, в третьих подчеркивается разница физического содержания обсуждаемых выражений. Поскольку элементарный электрический заряд 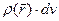 в выражении (1) умножается на значение потенциала электростатического поля в той же самой точке пространства
в выражении (1) умножается на значение потенциала электростатического поля в той же самой точке пространства 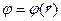 , представляется достаточно убедительным заключение, что выражение (1) описывает полную энергию системы электрических зарядов, а не только энергию попарного взаимодействия зарядов между собой.
, представляется достаточно убедительным заключение, что выражение (1) описывает полную энергию системы электрических зарядов, а не только энергию попарного взаимодействия зарядов между собой.
Дата добавления: 2017-09-01; просмотров: 2997;











