I.5.2 ПОТЕНЦИАЛ ПОЛЯ

В силу потенциальности гравитационного поля можно ввести его энергетическую характеристику – потенциал. Потенциалом гравитационного поля называется скалярная величина 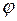, равная отношению потенциальной энергии 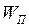материальной точки, помещённой в рассматриваемую точку поля, к массе 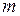материальной точки:

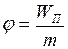. (I.130)

Потенциал не зависит от массы материальной точки, а является функцией координат точек гравитационного поля. Например, потенциал гравитационного поля, создаваемого неподвижной материальной точкой массы :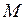

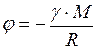, (I.131)

где 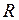- расстояние от источника поля до рассматриваемой точки.

Из формулы (I.131) вытекает, что геометрическое место точек с одинаковым потенциалом образуют сферическую поверхность 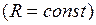. Такие поверхности, для которых потенциал постоянен, называются эквипотенциальными.

Если потенциал гравитационного поля, создаётся произвольной системой из 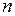неподвижных материальных точек, то при наложении гравитационных полей их потенциалы складываются алгебраически, т. е. потенциал 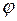в любой точке результирующего поля равен алгебраической сумме потенциалов в той же точке для всех накладывающихся полей порознь:

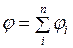. (I.132)

При пользовании формулой (I.132) необходимо, чтобы начала отсчётов потенциалов 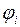всех накладывающихся полей были выбраны одинаково: .

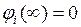Существует взаимосвязь между потенциалом поля тяготения и его напряжённостью:

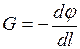. (I.133)

Величина 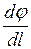характеризует изменение потенциала на единицу длины в направлении перемещения в поле тяготения и носит название градиента потенциала.

Связь между потенциалом поля тяготения и его напряжённостью, можно представить и в другом виде:

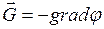, (I.134)

где 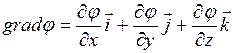- градиент скаляра 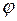( 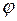- векторный дифференциальный оператор). Знак минус в формуле (I.134) указывает, что вектор напряжённости направлен в сторону убывания потенциала.