Евклидово точечное и n – мерное пространства
Определение 1: аффинное пространство 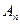 называется евклидовым точечным или просто евклидовым пространством, если связанное с ним пространство
называется евклидовым точечным или просто евклидовым пространством, если связанное с ним пространство 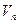 является евклидовым векторным пространством и обозначается
является евклидовым векторным пространством и обозначается 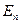 .
.
Замечание 1: точки и векторы являются основными объектами пространства 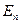 , а операции над ними называются основными или неопределяемыми отношениями. Природа основных объектов может быть любой, требуется лишь, чтобы основные отношения удовлетворяли аксиомам всех пяти групп. Все другие объекты и отношения определяются через основные, а при доказательствах теорем используются лишь аксиомы и ранее доказанные их следствия. Все определения и теоремы, сформулированные для пространства
, а операции над ними называются основными или неопределяемыми отношениями. Природа основных объектов может быть любой, требуется лишь, чтобы основные отношения удовлетворяли аксиомам всех пяти групп. Все другие объекты и отношения определяются через основные, а при доказательствах теорем используются лишь аксиомы и ранее доказанные их следствия. Все определения и теоремы, сформулированные для пространства 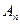 верны и для пространства
верны и для пространства 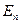 .
.
Определение 2: аффинная система координат в пространстве 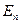 называется прямоугольной декартовой, если её координатные векторы
называется прямоугольной декартовой, если её координатные векторы 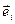 ,
, 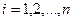 , образуют ортонормированный базис, связанного с ним евклидова векторного пространства
, образуют ортонормированный базис, связанного с ним евклидова векторного пространства 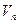 .
.
Теорема 1: при переходе от одной из двух прямоугольных декартовых систем координат к другой координаты 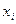 произвольной точки в старой системе выражаются через её координаты
произвольной точки в старой системе выражаются через её координаты 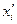 в новой системе координат формулами:
в новой системе координат формулами:
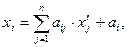
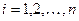 (1)
(1)
где 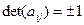 (то есть матрицы ортогональны).
(то есть матрицы ортогональны).
Эта теорема следует из теоремы (2) §2 и теоремы (3) §10, коэффициенты 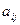 и
и 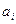 имеют прежний геометрический смысл.
имеют прежний геометрический смысл.
Пример 2: n=2, 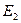 – евклидово пространство, формулы перехода известны из аналитической геометрии и являются частным случаем формул (1):
– евклидово пространство, формулы перехода известны из аналитической геометрии и являются частным случаем формул (1):

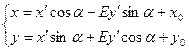 ,
, 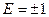 ,
,
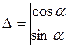
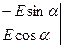 =
= 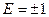 .
.
Определение 3: расстоянием от точки 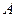 до точки
до точки 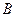 пространства
пространства 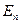 называется длина вектора
называется длина вектора 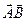 и обозначается
и обозначается 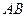 .
.
Пусть 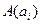 ,
, 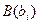 в одной из прямоугольных декартовых систем координат
в одной из прямоугольных декартовых систем координат 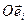 , тогда, очевидно:
, тогда, очевидно:
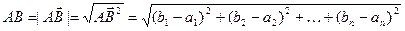
Теорема 2: для любых трёх точек 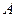 ,
, 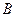 и
и 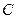 справедливо неравенство треугольника:
справедливо неравенство треугольника:
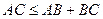 (2)
(2)
□ По аксиоме треугольника из параграфа §1 имеем: 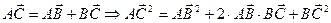 или
или 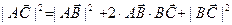 .
.
Так как 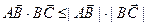 (при
(при 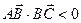 это очевидно, а при
это очевидно, а при  следует из неравенства Коши – Буняковского, замечание (1), §10), то
следует из неравенства Коши – Буняковского, замечание (1), §10), то
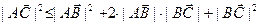 ,
, 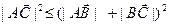 ,
, 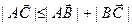 то есть
то есть 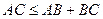 . ■
. ■
Замечание 2: очевидно, если 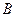 совпадает с
совпадает с 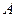 или
или 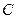 , то в формуле (2) имеет место знак равенства. Если же
, то в формуле (2) имеет место знак равенства. Если же 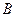 не совпадает ни с
не совпадает ни с 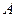 , ни с
, ни с 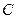 , то равенство выполняется тогда и только тогда, когда
, то равенство выполняется тогда и только тогда, когда 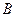 лежит на прямой
лежит на прямой 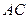 между точками
между точками 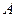 и
и 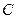 .
.
Определение 4: множество точек пространства 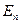 , расстояния от которых до данной точки
, расстояния от которых до данной точки 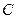 равны
равны 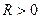 , называется гиперсферой с центром
, называется гиперсферой с центром 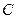 и радиусом
и радиусом 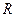 .
.
Если 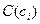 , а
, а 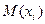 - точка гиперсферы, то имеем
- точка гиперсферы, то имеем 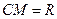 и
и
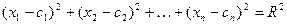 (3)
(3)
Определение 5: множество точек пространства 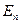 , расстояния от которых до данной точки
, расстояния от которых до данной точки 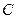 не превышает
не превышает 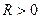 , называется n – мерным шаром. Очевидно, n – мерный шар задаётся в пространстве
, называется n – мерным шаром. Очевидно, n – мерный шар задаётся в пространстве 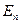 неравенством:
неравенством:
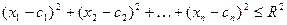 (4)
(4)
Примеры (частные случаи):
 1)n = 1,
1)n = 1, 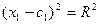
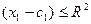
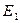 - прямая,
- прямая, 
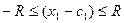
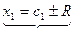
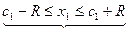
пара точек отрезок длины 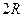

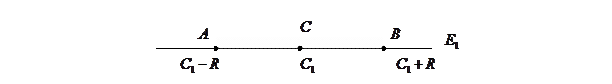
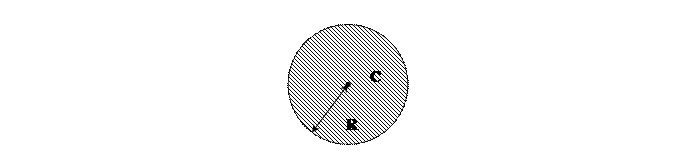
2)n = 2, E 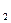 - плоскость:
- плоскость:
(x  - c
- c  )
) 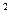 + (x
+ (x 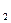 - c
- c 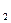 )
) 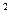 = R
= R 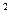 - окружность (x
- окружность (x 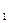 - c
- c 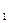 )
) 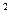 + (x
+ (x 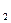 - c
- c 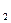 )
) 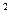
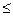 R
R  - круг
- круг
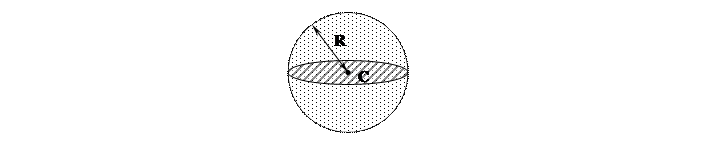
3)n=3, E  :
:
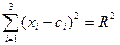 - сфера
- сфера 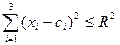 - шар
- шар
Определение 6: r-мерный параллелепипед пространства E  называется r-мерный кубом, если он натянут на точку А и единичные попарно ортогональные векторы:
называется r-мерный кубом, если он натянут на точку А и единичные попарно ортогональные векторы:
 = t
= t 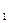
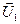 + t
+ t 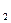
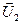 +…+ t
+…+ t 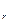
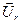 , 1
, 1 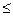 r
r 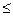 n,
n,
0 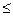 t
t 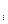
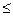 1, i =1,2,3,…r,
1, i =1,2,3,…r, 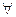 M
M 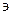 E
E 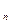 ,
, 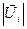 =1,
=1, 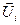
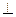
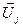 , i
, i 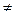 j.
j.
Примеры (частные случаи):
1) r =1 - отрезок длины 1:
A 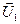 B AB=1
B AB=1

2) r = 2 - квадрат со стороной 1:

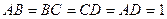 .
.
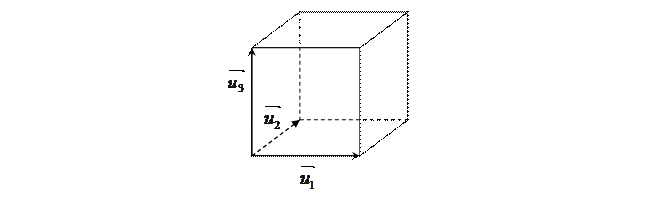
3) r =8 – куб с ребром 1:
Георг Кантор (1872) создал теорию точечных множеств в евклидовом пространстве по аналогии с теорией функций действительного переменного. Понятие верхнего и нижнего предела точечных множеств возникло по аналогии с понятием верхнего и нижнего предела функций. Кантор опирался также на теорию функций комплексного переменного, сформулированную Риманом. Кантор сформулировал в теории множеств  операцию включения одного множества в другое по аналогии с операцией делимости одного числового поля на другое, операцию пересечения множеств – по аналогии с нахождением наибольшего общего делителя двух числовых полей, а операцию суммирования двух множеств – по аналогии с определением наименьшего общего кратного. Кроме того, Кантор использовал аналогию с теорией тригонометрических рядов. Элементы теории множеств проглядывали сквозь проблемы о множестве точек, в которых сходится или расходится тригонометрический ряд данной функции (Ф.А.Медведев, «Очерки истории теории функций действительного переменного», 1975).
операцию включения одного множества в другое по аналогии с операцией делимости одного числового поля на другое, операцию пересечения множеств – по аналогии с нахождением наибольшего общего делителя двух числовых полей, а операцию суммирования двух множеств – по аналогии с определением наименьшего общего кратного. Кроме того, Кантор использовал аналогию с теорией тригонометрических рядов. Элементы теории множеств проглядывали сквозь проблемы о множестве точек, в которых сходится или расходится тригонометрический ряд данной функции (Ф.А.Медведев, «Очерки истории теории функций действительного переменного», 1975).
Дата добавления: 2021-09-07; просмотров: 636;











