Открытые и замкнутые множества
Множество M на прямой называется открытым, если каждая его точка сожержится в этом множестве вместе с некоторым интервалом. Замкнутым называется множество, содержащее все свои предельные точки (т. е. такие, что любой интервал, содержащий эту точку, пересекается со множеством еще хотя бы по одной точке). Например, отрезок является замкнутым множеством, но не является открытым, а интервал, наоборот, является открытым множеством, но не является замкнутым. Бывают множества, которые не являются ни открытыми, ни замкнутыми (например, полуинтервал). Существуют два множества, которые одновременно и замкнутые, и открытые – это пустое и все Z (докажите, что других нет). Легко видеть, что если M открыто, то [M] (или Z \ M – дополнение к множеству M до Z) замкнуто. Действительно, если [M] не замкнуто, то оно не содержит какую-то свою предельную точку m. Но тогда m M, причем каждый интервал, содержащийm, пересекается с множеством [M], т. е. имеет точку, не лежащую в M, а это противоречит тому, что M – открытое. Аналогично, тоже прямо из определения, доказывается, что если M замкнуто, то [M] открыто (проверьте!).
Теперь докажем следующую важную теорему.
Теорема. Любое открытое множество M можно представить в виде объединения интервалов с рациональными концами (т. е. с концами в рациональных точках).
Доказательство. Рассмотрим объединение U всех интервалов с рациональными концами, являющихся подмножествами нашего множества. Докажем, что это объединение совпадает со всем множеством. Действительно, если m – какая-то точка из M, то существует интервал (m1, m2) M, содержащий m (это следует из того, что M – открытое). На любом интервале можно найти рациональную точку. Пусть на (m1, m) – это m3, на (m, m2) – это m4. Тогда точка m покрыта объединением U, а именно, интервалом (m3, m4). Таким образом, мы доказали, что каждая точка m из Mпокрыта объединением U. Кроме того, как очевидно следует из построения U, никакая точка, не содержащаяся в M, не покрыта U. Значит, U и M совпадают.
Важным следствием из этой теоремы является тот факт, что любое открытое множество есть счетное объединение интервалов.
Нигде не~плотные множества и~множества меры~ноль. Канторово множество>
Одна из основных задач теории точечных множеств — изучение свойств различных типов точечных множеств. Познакомимся с этой теорией на двух примерах и изучим свойства так называемых замкнутых и открытых множеств.
Множество называется замкнутым, если оно содержит все свои предельные точки. Если множество не имеет ни одной предельной точки, то его тоже принято считать замкнутым. Кроме своих предельных точек, замкнутое множество может также содержать изолированные точки. Множество называется открытым, если каждая его точка является для него внутренней.
Приведем примеры замкнутых и открытых множеств. Всякий отрезок  есть замкнутое множество, а всякий интервал
есть замкнутое множество, а всякий интервал 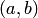 — открытое множество. Несобственные полуинтервалы
— открытое множество. Несобственные полуинтервалы 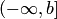 и
и 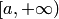 замкнуты, а несобственные интервалы
замкнуты, а несобственные интервалы 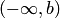 и
и  открыты. Вся прямая является одновременно и замкнутым и открытым множеством. Удобно считать пустое множество тоже одновременно замкнутым и открытым. Любое конечное множество точек на прямой замкнуто, так как оно не имеет предельных точек. Множество, состоящее из точек
открыты. Вся прямая является одновременно и замкнутым и открытым множеством. Удобно считать пустое множество тоже одновременно замкнутым и открытым. Любое конечное множество точек на прямой замкнуто, так как оно не имеет предельных точек. Множество, состоящее из точек
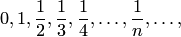
замкнуто; это множество имеет единственную предельную точку 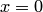 , которая принадлежит множеству.
, которая принадлежит множеству.
Наша задача состоит в том, чтобы выяснить, как устроено произвольное замкнутое или открытое множество. Для этого нам понадобится ряд вспомогательных фактов, которые мы примем без доказательства.
1. Пересечение любого числа замкнутых множеств замкнуто.
2. Сумма любого числа открытых множеств есть открытое множество.
3. Если замкнутое множество ограничено сверху, то оно содержит свою верхнюю грань. Аналогично, если замкнутое множество ограничено снизу, то оно содержит свою нижнюю грань.
Пусть  — произвольное множество точек на прямой. Назовем дополнением множества
— произвольное множество точек на прямой. Назовем дополнением множества  и обозначим через
и обозначим через 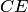 множество всех точек па прямой, не принадлежащих множеству
множество всех точек па прямой, не принадлежащих множеству 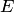 . Ясно, что если
. Ясно, что если 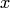 есть внешняя точка для
есть внешняя точка для 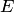 , то она является внутренней точкой для множества
, то она является внутренней точкой для множества 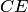 и обратно.
и обратно.
4. Если множество 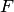 замкнуто, то его дополнение
замкнуто, то его дополнение 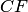 открыто и обратно.
открыто и обратно.
Предложение 4 показывает, что между замкнутыми и открытыми множествами имеется весьма тесная связь: одни являются дополнениями других. В силу этого достаточно изучить одни замкнутые или одни открытые множества. Знание свойств множеств одного типа позволяет сразу выяснить свойства множеств другого типа. Например, всякое открытое множество получается путем удаления из прямой некоторого замкнутого множества.
Приступаем к изучению свойств замкнутых множеств. Введем одно определение. Пусть 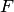 — замкнутое множество. Интервал
— замкнутое множество. Интервал 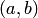 , обладающий тем свойством, что ни одна из его точек не принадлежит множеству
, обладающий тем свойством, что ни одна из его точек не принадлежит множеству 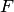 , а точки
, а точки  и
и 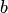 принадлежат
принадлежат 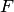 , называется смежным интервалом множества
, называется смежным интервалом множества 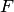 . К числу смежных интервалов мы будем также относить несобственные интервалы
. К числу смежных интервалов мы будем также относить несобственные интервалы  или
или 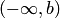 , если точка
, если точка  или точка
или точка 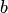 принадлежит множеству
принадлежит множеству 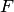 , а сами интервалы с
, а сами интервалы с 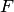 не пересекаются. Покажем, что если точка
не пересекаются. Покажем, что если точка 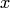 не принадлежит замкнутому множеству
не принадлежит замкнутому множеству 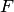 , то она принадлежит одному из его смежных интервалов.
, то она принадлежит одному из его смежных интервалов.
Обозначим через 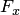 часть множества
часть множества 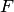 , расположенную правее точки
, расположенную правее точки 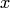 . Так как сама точка
. Так как сама точка 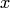 не принадлежит множеству
не принадлежит множеству 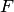 , то
, то 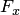 можно представить в форме пересечения
можно представить в форме пересечения 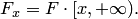
Каждое из множеств 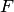 и
и 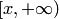 замкнуто. Поэтому, в силу предложения 1, множество
замкнуто. Поэтому, в силу предложения 1, множество 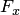 замкнуто. Если множество
замкнуто. Если множество 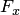 пусто, то весь полуинтервал
пусто, то весь полуинтервал 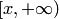 не принадлежит множеству
не принадлежит множеству 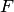 . Допустим теперь, что множество
. Допустим теперь, что множество 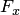 не пусто. Так как это множество целиком расположено на полуинтервале
не пусто. Так как это множество целиком расположено на полуинтервале 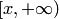 , то оно ограничено снизу. Обозначим через
, то оно ограничено снизу. Обозначим через 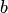 его нижнюю грань. Согласно предложению 3,
его нижнюю грань. Согласно предложению 3, 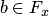 , а значит
, а значит 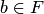 . Далее, так как
. Далее, так как 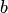 есть нижняя грань множества
есть нижняя грань множества 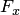 , то полуинтервал
, то полуинтервал  , лежащий левее точки
, лежащий левее точки 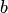 , не содержит точек множества
, не содержит точек множества 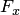 и, следовательно, не содержит точек множества
и, следовательно, не содержит точек множества 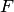 . Итак, мы построили полуинтервал
. Итак, мы построили полуинтервал  , не содержащий точек множества
, не содержащий точек множества 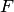 , причем либо
, причем либо 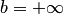 , либо точка
, либо точка 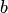 принадлежит множеству
принадлежит множеству 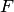 . Аналогично строится полуинтервал
. Аналогично строится полуинтервал 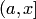 , не содержащий точек множества
, не содержащий точек множества 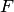 , причем либо
, причем либо 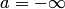 , либо
, либо  . Теперь ясно, что интервал
. Теперь ясно, что интервал 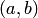 содержит точку
содержит точку 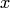 и является смежным интервалом множества
и является смежным интервалом множества 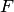 . Легко видеть, что если
. Легко видеть, что если 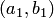 и
и 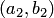 — два смежных интервала множества
— два смежных интервала множества 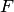 , то эти интервалы либо совпадают, либо не пересекаются.
, то эти интервалы либо совпадают, либо не пересекаются.
Из предыдущего следует, что всякое замкнутое множество на прямой получается путем удаления из прямой некоторого числа интервалов, а именно смежных интервалов множества 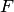 . Так как каждый интервал содержит по крайней мере одну рациональную точку, а всех рациональных точек на прямой — счетное множество, то легко убедиться, что число всех смежных интервалов не более чем счётно. Отсюда получаем окончательный вывод. Всякое замкнутое множество на прямой получается путем удаления из прямой не более чем счетного множества непересекающихся интервалов.
. Так как каждый интервал содержит по крайней мере одну рациональную точку, а всех рациональных точек на прямой — счетное множество, то легко убедиться, что число всех смежных интервалов не более чем счётно. Отсюда получаем окончательный вывод. Всякое замкнутое множество на прямой получается путем удаления из прямой не более чем счетного множества непересекающихся интервалов.
В силу предложения 4, отсюда сразу вытекает, что всякое открытое множество на прямой представляет собой не более чем счетную сумму непересекающихся интервалов. В силу предложений 1 и 2, ясно также, что всякое множество, устроенное, как указано выше, действительно является замкнутым (открытым).
Открытые и замкнутые множества
Перед тем, как приступить к постановке определений и задач, напомним значение используемых обозначений и кванторов:
∈ — принадлежит
∅ — пустое множество
Ε — множество действительных чисел
х* — закреплённая точка
А* — множество граничных точек
: — такое, что
⇒ — следовательно
∀ — для каждого
∃ — существует
Uε(х) — окрестность х по ε
Uºε(х) — проколотая окрестность х по ε
Итак,
Определение 1: Множество М ∈ Ε называется открытым, если для любого у ∈ М найдётся такое ε > 0, что окрестность y по ε строго меньше М
С помощью кванторов определение запишется следующим образом:
М ∈ Ε — открытое, если ∀ у∈М ∃ ε>0 : Uε(y) < M
Простым языком — открытое множество состоит из внутренних точек. Примерами открытого множества являются пустое множество, прямая, интервал (а, b)
Определение 2: Точка x* ∈ E называется граничной точкой множества М, если в любой окрестности точки х содержатся точки как из множества М, так и из его дополнения.
Теперь с помощью кванторов:
х*∈ E — граничная точка, если ∀Uε(x) ∩ М ≠ ∅ и ∀Uε(x) ∩ Е\М
Определение 3: Множество называется замкнутым, если ему принадлежат все граничные точки. Пример — отрезок [a, b]
Стоит отметить, что существуют множества, которые одновременно и открытые, и замкнутые. Это, например, всё множество действительных чисел и пустое множество (позднее будет доказано, что это 2 возможных и единственных случая).
Докажем несколько теорем, связанных с открытым и замкнутым множествами.
Теорема 1: Пусть множество А — открытое. Тогда дополнение к множеству А является замкнутым множеством.
Доказательство: Обозначим дополнение множества А как множество В:
В = Е\А
Доказывать будем от противного.
Предположим, что В — незамкнутое. Тогда существует граничная точка х*, которая не принадлежит В, а значит — принадлежит А. По определению граничной точки окрестность х* имеет пересечение как с В, так и с А. Однако с другой стороны х* является внутренней точкой открытого множества А, поэтому вся окрестность точки х* лежит в А. Отсюда делаем вывод, что множества А и В пересекаются не по пустому множеству. Такого быть не может, поэтому наше предположение неверно и В является замкнутым множеством, ч. т. д.
В кванторах доказательство можно записать короче:
Предположим, что В — незамкнутое, тогда:
(1) ∃ х∈А*:х∈A ⇒ ∀Uε(x) ∩ В ≠ ∅ (определение граничной точки)
(2) ∃ х∈А*:х∈A ⇒ ∀Uε(x) ⊂ А ≠ ∅ (определение открытоко множества)
Из (1) и (2) ⇒ А ∩ В ≠ ∅. Но А ∩ В = А ∩ Е\А = 0. Противоречие. В — замкнутое, ч. т. д.
Теорема 2: Пусть множество А — замкнутое. Тогда дополнение к множеству А является открытым множеством.
Доказательство: Обозначим дополнение множества А как множество В:
В = Е\А
Доказывать будем от противного.
Предположим, что В — замкнутое множество. Тогда любая граничная точка лежит в В. Но так как А — также замкнутое множество, то все граничные точки принадлежат и ему. Однако точка не может одновременно принадлежать множеству и его дополнению. Противоречие. В — открытое множество, ч. т. д.
В кванторах это выглядеть будет следующим образом:
Предположим, что В — замкнутое, тогда:
(1) ∀ х∈А*:х∈A (из условия)
(1) ∀ х∈А*:х∈В (из предположения)
Из (1) и (2) ⇒ А ∩ В ≠ ∅. Но А ∩ В = А ∩ Е\А = 0. Противоречие. В — открытое, ч. т. д.
Теорема 3: Пусть множество А — замкнутое и открытое. Тогда А = Е или А = ∅
Доказательство: Начнём записывать подробно, но сразу использую кванторы.
Предположим, что множество С — замкнутое и открытое, причём С ≠ ∅ и С ≠ Е. Тогда очевидно, что С ⊆ Е.
(1) ∃ х∈А*:х∈С ⇒ ∀Uε(x) ∩ Е\С ≠ ∅ (определение граничной точки, которая принадлежит С)
(2) ∃ х∈А*:х∈A ⇒ ∀Uε(x) ⊂ В (определение открытого множества С)
Из (1) и (2) следует, что Е\С ∩ С ≠ ∅, но это неверно. Противоречие. С не может быть одновременно и открытым, и замкнутым, ч. т. д.
Сжимающее отображение
[править | править вики-текст]
Материал из Википедии — свободной энциклопедии
Сжимающее отображение — отображение метрического пространства в себя, уменьшающее расстояние между любыми двумя точками не менее чем в 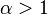 раз. Согласно теореме Банаха, у сжимающего отображения полного метрического пространства в себя существует неподвижная точка, причём ровно одна. Это утверждение, также называемое «принципом сжимающих отображений», широко используется при доказательстве различных математических утверждений.
раз. Согласно теореме Банаха, у сжимающего отображения полного метрического пространства в себя существует неподвижная точка, причём ровно одна. Это утверждение, также называемое «принципом сжимающих отображений», широко используется при доказательстве различных математических утверждений.
Пусть на метрическом пространстве 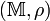 определён оператор
определён оператор 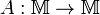 . Он называется сжимающим на
. Он называется сжимающим на 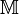 , если существует такое неотрицательное число
, если существует такое неотрицательное число  , что для любых двух точек
, что для любых двух точек 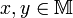 выполняется неравенство
выполняется неравенство
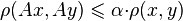 .
.
· При аффинном преобразовании прямая переходит в прямую.
· Если размерность пространства 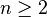 [источник не указан 1032 дня], то любое преобразование пространства (то есть биекция пространства на себя), которое переводит прямые в прямые, является аффинным. Это определение используется ваксиоматическом построении аффинной геометрии
[источник не указан 1032 дня], то любое преобразование пространства (то есть биекция пространства на себя), которое переводит прямые в прямые, является аффинным. Это определение используется ваксиоматическом построении аффинной геометрии
· Аффинные преобразования образуют группу относительно композиции.
· Любые три точки, не лежащие на одной прямой и их образы соответственно (не лежащие на одной прямой) однозначно задают аффинное преобразование плоскости.
Типы аффинных преобразований[править | править вики-текст]
· Эквиаффинное преобразование — аффинное преобразование, сохраняющее площадь (также, сохраняется аффинная длина).
· Центроаффинное преобразование — аффинное преобразование, сохраняющее начало координат.
Матричное представление[править | править вики-текст]
Как и другие проективные преобразования, аффинное преобразование 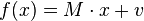 можно записать как матрицу перехода в однородных координатах:
можно записать как матрицу перехода в однородных координатах:
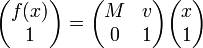
Матричное представление используется, в частности, для записи аффинных преобразований в компьютерной графике. Указанная выше форма используется в OpenGL[2]; в DirectX (где координаты представляются в виде матриц 1×4) онатранспонирована[3].
Вариации и обобщения[править | править вики-текст]
· В приведённом выше определении аффинного преобразования можно использовать любое поле, а не только поле вещественных чисел 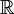 .
.
· Отображение между метрическими пространствами называется аффинным, если оно переводит геодезические в геодезические (с учётом параметризации).
· Аффинные преобразования пространства 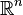 являются частным случаем проективных преобразований того же пространства. В свою очередь, проективные преобразования пространства
являются частным случаем проективных преобразований того же пространства. В свою очередь, проективные преобразования пространства 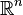 можно представить как аффинные преобразования пространства
можно представить как аффинные преобразования пространства 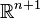 .
.
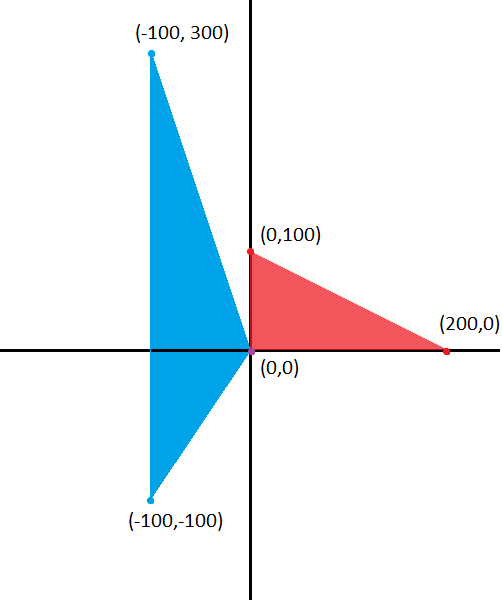
красный треугольник переходит в синий при аффинном преобразовании , если новые координаты отобразить в прежнем базисе
Метрика Хаусдорфа это естественная метрика, определённая на множестве всех непустых компактных подмножеств метрического пространства. Она превращает множество всех непустых компактных подмножеств метрического пространства в метрическое пространство.
Скорее всего, первое упоминание этой метрики содержится в книге Хаусдорфа «Теория множеств» (1914 г.). Двумя годами позже, та же метрика описывается в книге Бляшке «Круг и шар», возможно независимо, так как не содержит ссылки на книгу Хаусдорфа.
Пусть 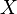 и
и 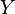 суть два непустых компактных подмножества метрического пространства
суть два непустых компактных подмножества метрического пространства 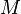 . Тогда расстояние по Хаусдорфу,
. Тогда расстояние по Хаусдорфу, 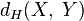 , между
, между 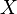 и
и 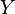 есть минимальное число
есть минимальное число  такое, что замкнутая
такое, что замкнутая  -окрестность
-окрестность 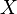 содержит
содержит 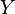 и также замкнутая
и также замкнутая  -окрестность
-окрестность 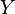 содержит
содержит 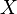 .
.
Другими словами, если 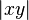 обозначает расстояние между точками
обозначает расстояние между точками 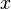 и
и 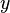 в
в 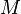 то
то
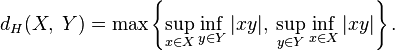
Свойства
Пусть 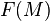 обозначает множество всех непустых компактных подмножеств метрического пространства
обозначает множество всех непустых компактных подмножеств метрического пространства 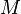 с метрикой Хаусдорфа:
с метрикой Хаусдорфа:
· Топология пространства 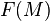 полностью определяется топологией
полностью определяется топологией 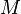 .
.
· (Теорема Бляшке) 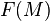 компактно тогда и только тогда, когда компактно
компактно тогда и только тогда, когда компактно 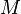 .
.
· 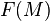 полно тогда и только тогда, когда
полно тогда и только тогда, когда 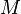 полное.
полное.
· Иногда метрика Хаусдорфа рассматривается на множестве всех замкнутых подмножеств метрического пространства. В этом случае расстояние между некоторыми подмножествами может равняться бесконечности.
· Иногда метрика Хаусдорфа рассматривается на множестве всех подмножеств метрического пространства. В этом случае она является только псевдо метрикой и не является метрикой, так как «расстояние» между различными подмножествами может равняться нулю.
· В евклидовой геометрии, часто применяется метрика Хаусдорфа с точностью до конгруэнтности. Пусть 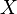 и
и 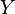 два компактных подмножества евклидова пространства, тогда определяется как минимум по всем движениям евклидова пространства . Строго говоря, эта метрика на пространстве классов конгруэнтности компактных подмножеств евклидова пространства.
два компактных подмножества евклидова пространства, тогда определяется как минимум по всем движениям евклидова пространства . Строго говоря, эта метрика на пространстве классов конгруэнтности компактных подмножеств евклидова пространства.
· Метрика Громова—Хаусдорфа аналогична метрике Хаусдорфа с точностью до конгруэнтности. Она превращает множество (изометрических классов) компактных метрических пространств в метрическое пространство.
Дата добавления: 2021-09-07; просмотров: 2130;











