Множества и отображения.

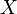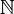В теории множеств, счётное мно́жество есть бесконечное множество, элементы которого возможно пронумеровать натуральными числами. Более формально: множество является счётным, если существует биекция , где обозначает множество всех натуральных чисел. Другими словами, счётное множество — это множество, равномощное множеству натуральных чисел.

Счётное множество является «наименьшим» бесконечным множеством, то есть в любом бесконечном множестве найдётся счётное подмножество. Мощность множества всех натуральных чисел обозначается символом 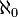(произносится: «алеф-нуль»)

Свойства

1. Любое подмножество счётного множества не более чем счётно (т.е. конечно или счётно).

2. Объединение конечного или счётного числа счётных множеств счётно.

3. Прямое произведение конечного числа счётных множеств счётно.

4. Множество всех конечных подмножеств счётного множества счётно.

5. Множество всех подмножеств счётного множества континуально и, в частности, не является счётным.

Счётные множества

· Простые числа Натуральные числа Целые числа Рациональные числа Алгебраические числа Кольцо периодов Вычислимые числа Арифметические числа

· Множество всех конечных слов над счётным алфавитом

· Множество всех слов над конечным алфавитом

· Любое бесконечное семейство непересекающихся открытых интервалов на действительной оси

· Множество всех прямых на плоскости, каждая из которых содержит хотя бы 2 точки с рациональными координатами

· Любое бесконечное множество точек на плоскости, все попарные расстояния между элементами которого рациональны

Несчётные множества[править | править вики-текст]

· Вещественные числа Комплексные числа Числа Кэли

Мощность множества

Рассмотрим множество всех молекул в земной атмосфере. Это множество содержит очень большое число элементов (примерно 1.02 77 010 541 0), но оно конечное, т.е. существует такая константа, которая больше числа элементов этого множества. Помимо конечных существуют бесконечные множества. Одной из задач теории множеств является определение числа элементов множества и исследование вопроса о сравнении друг с другом двух множеств по количеству элементов.

Для конечных множеств самой разной природы эта задача легко решается непосредственным подсчетом. Для бесконечных множеств вопрос о сравнении невозможно решить как для конечных, с помощью подсчета. Поэтому Кантор предложил для сравнения двух бесконечных множеств установить между ними взаимно однозначное (биективное) отображение. Рассмотрим примеры установления такого отображения.

Пример 1. В качестве множества А рассмотрим интервал на числовой прямой, пусть А=(-1, 1), а в качестве множества В - множество действительных чисел R. Это множества одинаковой мощности, т.к отображение f(x) = tg(px/2), хÎА позволяет установить между ними искомое взаимно-однозначное соответствие.

Пример 2. Пусть А = [-1,1], В = (-1,1). Строим отображение f : A ® B по следующему правилу: выделим в А последовательность -1, 1, 1/2, 1/3, 1/4, . . . , 1/n и положим f(-1)=1/2, f(1)=1/3, f(1/2)=1/4, f(1/3)=1/5, т.е. f(1/n) = 1/(n+2), а все точки, не входящие в эту последовательность отобразим сами в себя, т.е. f(x) = =x. Следовательно, открытый и замкнутый интервалы эквивалентны.

Мощность множества является обобщением понятия числа элементов множества. Если взаимно однозначное отображение множеств установлено, значит, по определению, в обоих множествах одинаковое число элементов или мощность одного множества равна мощности другого множества.

Мощность - это то общее, что есть у двух эквивалентных множеств. Мощность множества A обозначается m(A) или |A|. Таким образом, m(A)=m(B), если A~B.

Если множество A эквивалентно какому-либо подмножеству множества B, то мощность A не больше мощности B (т.е. m(A)£m(B)). Если при этом множество B не эквивалентно никакому подмножеству множества A, то m(A)< m(B).

Простейшим среди бесконечных множеств является множество натуральных чисел N.

ОПРЕДЕЛЕНИЕ. Назовем счетным всякое множество, эквивалентное множеству N. Другими словами, счетным называется всякое множество, элементы которого можно перенумеровать или составить из них бесконечную последовательность.

Примеры счетных множеств.

1. Множество целых чисел Z={0, ±1, ±2, . . .}.Построим из его элементов последовательность: a₁=0; a₂=-1; a₃=1; a₄=-2; a₅=2; . . . Формулу для вычисления ее общего члена можно записать в виде

2. Множество Q всех рациональных чисел.

Докажем счетность этого множества. Как известно, рациональные числа - это дроби вида p/q, где pÎZ, qÎN.

Запишем их в виде таблицы из бесконечного числа строк и столбцов

0/1®1/1 2/1®3/1 . . .

-1/1 -2/1 -3/1 -4/1 . . .

¯

1/2 2/2 3/2 4/2 . . .

-1/2 -2/2 -3/2 -4/2 . . .

. . . . . . . . . . . . .

Из элементов этой таблицы построим последовательность по следующему правилу a₁=0/1; a₂=1/1; a₃=-1/1; a₄=1/2; a₅=-2/1; a₆=2/1 и т.д., двигаясь в направлении, указанном стрелками. Очевидно, в эту последовательность войдут все рациональные числа. Более того, в ней многие числа будут повторяться. Следовательно, мощность множества элементов данной последовательности не меньше мощности множества рациональных чисел. С другой стороны, эта последовательность эквивалентна натуральному ряду, т.е. подмножеству множества Q, а значит она не может иметь мощность, большую чем Q. Значит, множество рациональных чисел счетно.

Бесконечное множество, не являющееся счетным называется несчетным.

1. Всякое подмножество счетного множества конечно или счетно.

Доказательство. Пусть А - счетное множество и BÍА. Поскольку А счетно, то занумеруем его элементы и построим из них последовательность

a₁, a₂, a₃, . . .

Из этой последовательности выделим все элементы, принадлежащие множеству B, т.е. рассмотрим последовательность

a_n1, a_n2, a_n3, . . .

Возможны следующие случаи:

1) множество B конечно;

2) множество B бесконечно.

Поскольку элементы множества B занумерованы, то во втором случае оно является счетным, что и требовалось доказать.

2. Объединение любого конечного или счетного множества счетных множеств снова является счетным.

ДОКАЗАТЕЛЬСТВО. Пусть множества А₁, A₂, . . . , А_n, . . . – счетные. Если их число не более, чем счетно, то множества можно занумеровать и расположить принадлежащие им элементы в таблицу

А₁={a₁₁, a₁₂, a₁₃, . . .} А₂={a₂₁, a₂₂, a₂₃, . . .} А₃={a₃₁, a₃₂, a₃₃, . . .}

. . . . . . . . . . . . . . . . .

Пусть B= 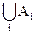. Построим последовательность подобно тому, как это было сделано в п. 4 при доказательстве счетности Q.

b₁=a₁₁, b₂=a₁₂, b₃=a₂₁, b₄=a₃₁, b₅=a₂₂, . . . (1)

Если множества А_i попарно пересекаются (А_i ÇА_j ¹Æ), то в последовательность (1) не включаются те элементы, которые уже занумерованы. Таким образом, построено взаимно однозначное соответствие между множествами B и N. Следовательно, множество B счетно.

3. Всякое бесконечное множество содержит счетное подмножество.

ДОКАЗАТЕЛЬСТВО. Пусть М - произвольное бесконечное множество. Выберем в нем произвольный первый элемент и обозначим его a₁ , затем - элемент a₂ и т.д. Получаем последовательность a₁, a₂, . . . , которая не может оборваться на каком-то элементе, так как М бесконечно. Следовательно, данная последовательность образует счетное подмножество множества М.

Доказанная теорема позволяет утверждать, что среди бесконечных множеств счетное множество является самым "маленьким".

Если множество конечно или счетно то говорят, что оно не более, чем счетно.

Рассмотренные примеры и свойства могут создать впечатление, что все бесконечные множества счетны. Однако, это далеко не так, и для доказательства этого достаточно построить контрпример, т.е. предъявить бесконечное множество, не являющееся счетным.

ТЕОРЕМА. Множество всех бесконечных бинарных последовательностей, т.е. состоящих из 0 и 1, несчетно.

ДОКАЗАТЕЛЬСТВО. Предположим противное, т.е. что эти последовательности можно занумеровать. Пусть P₁, P₂, . . . - последовательности, где P₁={a₁₁, a₁₂, a₁₃, . . .}, P₂={a₂₁, a₂₂, a₂₃, . . .} и т.д., где а_ij=0 или а_ij=1.

Построим последовательность P, не содержащуюся в этом списке. Такая последовательность существует, например, P={1-a₁₁, 1-a₂₂, 1-a₃₃, . . .}. Очевидно, что ее элементы равны 0 или 1, причем она не равна никакой другой из списка, потому что отличается от последовательности P₁ по крайней мере первым элементом, от P₂ - по крайней мере вторым и т.д. Таким образом, построенная последовательность отличается от любой из занумерованных последовательностей хотя бы одним элементом. Следовательно, множество всех бинарных последовательностей занумеровать невозможно, а это означает, что оно несчетно.

Самое интересное в теории множеств то, что она рассматривает не только конечные множества – множества, содержащие конечное число элементов, но и бесконечные, для которых даже понятие числа бессмыс­ленно. Таким образом, теория множеств может рассматривать не только множест­во студентов в группе, но и множество точек на прямой, и множество звёзд на небе.

До Кантора математики признавали и использовали так называемую потенциальную бесконечность. Самый яркий пример – это по­нятие бесконечно большого числа в высшей математике: бесконечно большое число – это число, которое больше любого, наперёд заданного.

Кантор позволил себе в математике актуальную бесконечность. По Кантору, бесконечность существует сразу вся. А раз бесконечные мно­жества есть, и сразу целиком, то с ними можно производить математиче­ские манипуляции, например, сравнивать.

Кантор доказал теорему, из которой следует, что бесконечности могут быть раз­ные по величине. Поскольку «число» и «количество» – термины в этом случае неуместные, то он ввёл понятие «мощность множества». Множества равномощны, если между их элементами можно установить взаимнооднозначное соответствие.

Обратимся для наглядности к числам. Пересчитывая что-то, мы используем целые (положительные) числа 1, 2, 3 ..., которые называют натуральными. Мы знаем, что чисел нам хва­тит для пересчёта чего угодно. Мы также знаем, что это множество бесконечное. Кантор назвал это множествосчётным, а его мощность – мощно­стью счётного множества. Мощность этого множества Кантор взял за эталон и стал сравнивать её с мощностями других множеств. Во-первых, он установил, что эта мощ­ность больше мощности любого конечного множества. Во-вторых, он доказал, что многие бесконечные множества имеют ту же мощность (то же «количество» элементов), что и счётное.

Один из самых поразительных примеров, что множество целых положительных чисел имеет столько же элементов, сколько и мно­жество целых чётных положительных чисел, т.е. они равномощны(!).

Действительно, запишем друг под другом:

1 2 3 4...

2 4 6 8...

Из этой записи видно, что обе последовательности имеют одинаковое количество элементов, поскольку любому числу первой, всегда соответствует стро­го одно число второй последовательности. Так что вторая последователь­ность не может исчерпаться раньше первой, и наоборот. Следовательно, эти множества равномощны, и здесь часть равна целому. Мы получили один из парадоксов.

Если построить множество всех подмножеств конкретного множест­ва, то всегда получим множество больше исходного. Кантор доказал, что если взять бесконечное множество счётной мощности, например, множество целых положительных чисел, и умозрительно построить множество, содержащее в качестве элементов все под­множества этого множества, то получим мощность большую, чем счёт­ная мощность. В принципе не существует способа пересчитать (пусть в бесконечности) такое множество. В нём всегда больше элементов. Эта но­вая большая мощность называется мощностью континуума.

И вновь парадокс. Мощность континуума имеет, например, множество то­чек прямой. Более того, любой отрезок числовой оси, даже отрезок от 0 до 1, имеет мощность континуума, то есть на нём больше чисел, чем найдётся чисел в счётном множестве. А раз этот отрезок имеет мощность континуума, как и вся (бес­конечная) прямая и, естественно, любой её отрезок, то можно сказать, что на отрезке от 0 до 1 ровно столько же точек, сколько на отрезке прямой от Земли до Юпитера. Здесь тоже часть равна целому, если и часть и целое имеют мощ­ность континуума. И все они одинаково больше числа звёзд на небе или числа всевозможных алгоритмов...

Конти́нуум в теории множеств — мощность (или кардинальное число) множества всех вещественных чисел. Обозначается строчной латинской буквой c во фрактурном начертании: . Множество, имеющее мощность континуум, называется континуа́льным множеством.

Также термин «континуум» может обозначать само множество вещественных чисел, или даже любое континуальное множество.

· Континуум является бесконечной мощностью (алефом), превосходящей мощность счётного множества 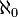. Любое континуальное множество имеет счётное подмножество.

· Континуум не меньше, чем мощность множества всех счётных ординалов 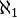. Любое континуальное множество имеет подмножество мощности 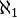. Предположение о том, что 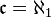называется континуум-гипотезой.

· Мощность объединения не более чем континуального семейства множеств, каждое из которых не более чем континуально, не превосходит континуума.

· При разбиении континуального множества на конечное или счётное число частей хотя бы одна из частей будет иметь мощность континуум. Как следствие, конфинальность (англ.) континуума — несчётна.

Примеры множеств, имеющих мощность континуум:

· Все точки отрезка .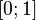

· Все точки плоскост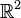и (или ), например — множество всех комплексных чисел.

· Множество всех иррациональных чисел.

· Множество всех трансцендентных чисел.

· Множество всех подмножеств счётного множества.

· Множество всех частичных порядков на счётном множестве.

· Множество всех счётных множеств натуральных чисел.

· Множество всех счётных множеств вещественных чисел.

· Множество всех непрерывных функций .

· Множество всех открытых подмножеств плоскост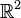и (или ).

· Множество всех замкнутых подмножеств плоскост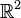и (или ).

· Множество всех борелевских подмножеств плоскост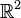и (или ).

· Канторово множество