ЗАМКНУТЫЕ МНОЖЕСТВА

Определение. Назовем точку 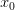предельной точкой множества 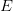, если в произвольной окрестности точки 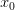существует хотя бы одна точка из 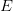, отличная от .
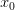Замечание. Если 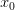– предельная точка множества 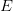, то в произвольной ее окрестности содержится бесконечное множество точек из .

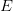Доказательство. Обозначим через 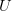произвольную окрестность 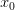. Предположим, что в этой окрестности содержится лишь конечное число точек множества 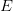, отличных от 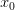. Тогда среди них найдется точка 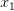, ближайшая к 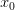. Но тогда в шаре радиуса 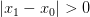с центром в 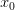нет ни одной точки из 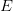, отличной от 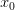, а это невозможно, поскольку 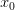– предельная точка множества .

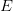Пример. Пусть 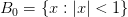– единичный шар. Очевидно, что любая точка этого шара является для него предельной. Если же 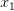находится на сфере, т. е. 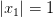, то она не принадлежит шару, но является предельной для шара. Действительно, пусть 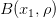— произвольная окрестность точки 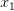. Тогда все точки вида 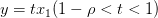принадлежат 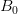и содержатся в 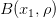. Следовательно, 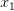является предельной для шара 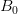по определению.

Рассмотрим теперь точку 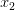, такую, что 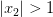. Докажем, что она не будет предельной для 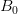. Действительно, предположим, что 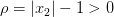. Тогда в 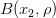нет ни одной точки из 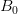. Это легко можно показать, используя неравенство треугольника. Поэтому точка 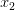не является предельной для множества .

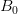Таким образом, можно видеть, что предельные точки множества могут как содержаться, так и не содержаться в нем.

Определение.Множество 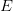называется замкнутым, если все его предельные точкисодержатся в нем.

Условимся считать пустое множество 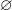замкнутым. Пространство 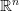, очевидно, является замкнутым по определению.

Точка 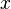называется предельной точкой подмножества 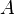в топологическом пространстве 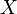, если всякая проколотая окрестность точки 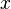имеет с 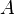непустое пересечение.

Точка 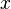называется строго предельной точкой подмножества 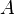, если всякая окрестность точки 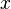имеет с 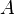бесконечное число общих точек. Для T₁-пространств (то есть пространств, у которых все точки (одноточечные множества) замкнуты) понятия предельная точка и строго предельная точка равносильны.

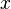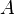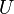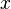Точка называется точкой полного накопления подмножества , если для всякой окрестности точки мощность пересечения 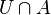равна мощности множества .

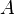Предельная точка числового множества[править | править вики-текст]

В частности, предельной точкой числового множества, имеющего бесконечное число элементов, называется точка числовой прямой, в любой окрестности которой содержится бесконечно много элементов этого множества. Также можно считать предельной точкой такого множества 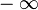, если из некоторых его элементов можно составить бесконечно большую последовательность с попарно различными отрицательными элементами. Если же можно составить бесконечно большую последовательность с попарно различными положительными элементами, то можно считать предельной точкой 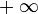.^[1]

Верхняя предельная точка числового множества — это наибольшая из его предельных точек.

Нижняя предельная точка числового множества — это наименьшая из его предельных точек.

Свойства[править | править вики-текст]

· У любого ограниченного числового множества, имеющего бесконечное число элементов, существуют и верхняя, и нижняя предельные точки (в множестве вещественных чисел). Если добавить в множество вещественных чисел 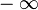и 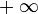, то в получившемся множестве предельные точки имеют вообще все числовые множества с бесконечным числом элементов.

· Из элементов любого ограниченного числового множества, имеющего бесконечное число элементов, можно выделить сходящуюся последовательность, элементы которой попарно различны.