Множества мощности континуума и выше
Другим важным примером бесконечного несчетного множества является множество вещественных чисел R. Дадим одно из возможных определений вещественного числа с помощью сечений Дедекинда.
Рассмотрим разбиение множества всех рациональных чисел на два непустых подмножества А и В. Будем называть это разбиение сечением и обозначать А|В, если выполняются условия:
10. Каждое рациональное число попадает в одно и только одно из множеств А или В.
20. Для всех xÎA и yÎB имеет место соотношение y > x.
Назовем А нижним классом сечения, В - верхним классом.
Существуют сечения трех типов.
1. Сечение, у которого в нижнем классе нет максимального числа, а в верхнем классе есть минимальное число, назовем сечением первого типа.
2. Сечение, у которого в нижнем классе есть максимальный элемент, а в верхнем классе нет минимального число, назовем сечением второго типа.
3. Сечение, у которого в нижнем классе нет максимального элемента, а в верхнем классе - минимального, назовем сечением третьего типа.
Примеры сечений:
1) А ={ x | x<1 }; B ={ x | x³1 } - сечение 1-го типа;
2) А ={ x | x£1 }; B ={ x | x>1 } - сечение 2-го типа;
3) А ={ x | x3£2 }; B ={ x | x3 >2 } - сечение 3-го типа.
Докажем что в третьем примере нижний класс не содержит максимальный элемент. Для этого покажем, что
" аÎA $ n>0 : (a + 1/n)3 < 2.
Так как (a+1/n)3<a3 +(3a2+3a+1)/n, то достаточно выбрать такое n, чтобы n>3a2/(2-a3). Иными словами, какое бы рациональное а из A мы ни выбрали, в классе А всегда можно найти число больше его.
Аналогично можно доказать, что в этом примере в верхнем классе нет минимального элемента.
Сечения типа 1 и 2 определяют рациональное число r. Для сечения 1 типа это число - наименьшее в верхнем классе, для сечения 2 типа - наибольшее в нижнем классе. Сечение 3 типа не определяет никакого рационального числа, так как предположение противного противоречит определению сечения.
Будем говорить, что сечение 3-го типа определяет иррациональное число a, если для любых рациональных чисел xÎA и yÎB выполняется неравенство x<a<y. Иррациональные числа - это множество чисел, каждое из которых определяется некоторым сечением 3-го типа. Множество действительных (вещественных) чисел – это множество рациональных и иррациональных чисел.
Для мощности множества вещественных чисел R есть специальное обозначение - с. Любое множество имеющее такую мощность называется континуумом (от английского continue - продолжаться).
Введение понятия мощность континуума порождает два вопроса.
1. Существует ли множество мощностью больше чем с?
2. Существует ли множество промежуточной мощности между счетным и континуумом?
На первый взгляд множеством мощности больше с является любая плоская фигура, например, квадрат. Однако, это не так и справедлива
ТЕОРЕМА. Единичный квадрат на плоскости имеет мощность равную с.
ДОКАЗАТЕЛЬСТВО. Построим отображение f точек квадрата на его сторону. Возьмем любую точку внутри квадрата с координатами (x,y). Пусть в десятичном представлении x=0,a1a2a3..., а y=0,b1b2b3... . Образуем число z=f(x,y)= =0,a1b1a2b2a3b3..., которое является координатой точки на стороне квадрата. Таким образом, мы отобразим точки квадрата на его сторону. Ясно что это отображение инъективно, т.е. если мы берем точки А=(x1, y1) и B=(x2, y2), такие, что А¹В, и определим zA=f(A), zB=f(B), то получим zA¹zB, т.е. две разные точки A и B квадрата отображаются в две разные точки на отрезке прямой. Действительно, пусть А¹В. Значит x1¹x2 или y1¹y2, а раз так то эти числа отличаются хотя бы одним десятичным знаком, и значит zA¹zB.
Инъективность означает, что точек в квадрате не больше, чем на отрезке. С другой стороны, их не может быть меньше, поскольку отрезок является подмножеством квадрата. Следовательно, построенное отображение f взаимно-однозначно.
Тем не менее множества мощности выше континуума существуют, более того, справедлива
ТЕОРЕМА. Для любого множества А существует множество В большей мощности.
ДОКАЗАТЕЛЬСТВО. Пусть имеется множество А. Рассмотрим множество В, являющееся множеством всех функций, определенных в точках множества А и равных 0 или 1 в этих точках. Покажем, что мощность множества В больше мощности А.
Рассмотрим на множестве А функцию из B, определенную по правилу
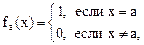
где aÎА. Поставим каждой точке аÎА в соответствие функция fa(x)ÎВ, причем, это отображение является взаимно однозначным. Очевидно, что построенное множество функций не исчерпывает всех возможных функций из В и {fa(x)}ÌВ, т.е. мы определили взаимно однозначное отображение всего А на часть множества В. Следовательно, мощность В не меньше мощности А.
Докажем, что мощность В не равна мощности А. Это эквивалентно тому, что не существует взаимно однозначного отображения А на все В. Предположим противное, что существует биективное отображение j : А ® В, которое каждому аÎА ставит в соответствие элемент bÎВ и каждой функции из B - элемент множества A. Обозначим j(a) = f(a)(x), и рассмотрим функцию
g(x) = 1 – f(x)(x).
По свойствам элементов множества В имеем, что значение f(x)(x) равно 0 или 1, тогда это свойство выполнено и для функции g(x). Следовательно, g(x)ÎВ. Значит, по предположению, существует такая точка bÎА, что ей однозначно соответствует g(x), т.е. g(x)=f(b)(x). Возьмем х=b, тогда получим
1 – f(b)(b) = f(b)(b).
Отсюда f(b)(b)=1/2, что противоречит условию принадлежности функции f(b)(x) множеству В. Поэтому, такого отображения j не существует. Значит, мощность В строго больше мощности А.
Из теоремы следует, что множества самой большой мощности не существует.
Эквивалентный способ построения множества большей мощности получим, если определим B как множество, элементами которого являются всевозможные подмножества множества A. Тогда m(B)= 2|A|.
Множество, мощность которого равна 2c, называется множеством мощности гиперконтинуума.
Что касается проблемы существования множества промежуточной мощности, то оказалось, что это утверждение невозможно доказать на основе аксиом теории множеств, но оно и не противоречит им.
Кольца и алгебры
Определение. Пусть  -- произвольное множество, на котором определены две бинарные операции: сложение
-- произвольное множество, на котором определены две бинарные операции: сложение 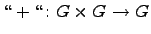 и умножение
и умножение 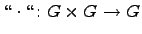 . Множество
. Множество  называется кольцом, если
называется кольцом, если
1) относительно сложения  является абелевой группой;
является абелевой группой;
2) операция умножения дистрибутивна, т.е. для любых 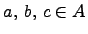 справедливы равенства
справедливы равенства 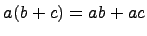 и
и 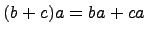 .
.
Определение.  Если операция умножения ассоциативна, т.е. для любых
Если операция умножения ассоциативна, т.е. для любых 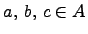 справедливо равенство
справедливо равенство 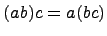 , то кольцо называется ассоциативным.
, то кольцо называется ассоциативным.
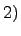 Если операция умножения коммутативна, т.е. для любых
Если операция умножения коммутативна, т.е. для любых 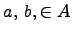 справедливо равенство
справедливо равенство 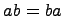 , то кольцо называется коммутативным.
, то кольцо называется коммутативным.
Если существует единица, т.е. такой элемент 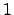 , что для любого
, что для любого 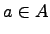 справедливо равенство
справедливо равенство 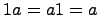 , то кольцо называется кольцом с единицей.
, то кольцо называется кольцом с единицей.
Коммутативное, ассоциативное кольцо с единицей, в котором каждый ненулевой элемент имеет обратный, называется полем.
Определение. Пусть  -- кольцо и линейное пространство над полем
-- кольцо и линейное пространство над полем 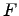 . Тогда
. Тогда  называется алгеброй, если
называется алгеброй, если 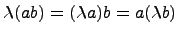 для любых
для любых 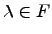 и
и 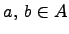 .
.
Пример.  Алгебра квадратных матриц над полем.
Алгебра квадратных матриц над полем.
Алгебра многочленов над полем 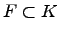 . Тогда
. Тогда 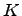 -- алгебра над
-- алгебра над 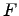 . Число
. Число 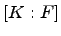 называется степенью расширения (т.е. это размерность
называется степенью расширения (т.е. это размерность 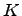 над
над 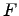 ).
).
Определение. Пусть 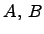 -- кольца. Тогда отображение
-- кольца. Тогда отображение 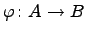 называется гомоморфизмом колец, если
называется гомоморфизмом колец, если 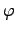 является гомоморфизмом абелевых групп и
является гомоморфизмом абелевых групп и 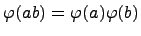 . Если
. Если 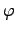 биективно, то
биективно, то 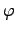 называется изоморфизмом.
называется изоморфизмом.
Определение. Пусть 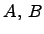 -- алгебры. Тогда отображение
-- алгебры. Тогда отображение 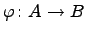 называетсягомоморфизмом алгебр, если
называетсягомоморфизмом алгебр, если 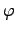 является гомоморфизмом колец и линейным отображением. Если
является гомоморфизмом колец и линейным отображением. Если 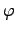 биективно, то
биективно, то 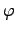 называется изоморфизмом.
называется изоморфизмом.
Пример. Пусть 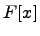 -- кольцо многочленов от одной переменной. Выберем
-- кольцо многочленов от одной переменной. Выберем 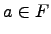 и зададим гомоморфизм
и зададим гомоморфизм 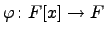 , положив
, положив 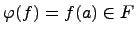 .
.
Пусть 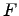 -- подполе в
-- подполе в 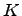 , и пусть
, и пусть 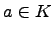 . Тогда продолжим
. Тогда продолжим 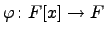 до
до 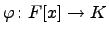 , положив
, положив 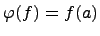 .
.
Например, если 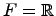 ,
, 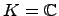 и
и 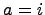 . Тогда
. Тогда 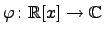 и
и 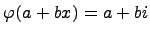 . Гомоморфизм
. Гомоморфизм 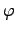 является эпиморфизмом.
является эпиморфизмом.
Определение. Ядро 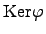 гомоморфизма колец
гомоморфизма колец 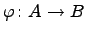 -- это ядро аддитивной группы, т.е.
-- это ядро аддитивной группы, т.е. 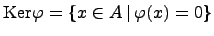 .
.
Определение. Подмножество 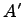 кольца
кольца  называется подкольцом, если
называется подкольцом, если 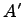 является подгруппой в аддитивной группе кольца
является подгруппой в аддитивной группе кольца  и из условия
и из условия 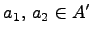 следует
следует 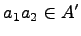 .
.
Определение. Подмножество 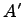 алгебры
алгебры  называется подалгеброй, если
называется подалгеброй, если 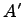 является подкольцом в кольце алгебры
является подкольцом в кольце алгебры  и из условия
и из условия 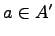 следует
следует 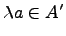 для любого
для любого 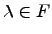 .
.
Определение. Подмножество 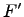 поля
поля 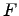 называется подполем, если
называется подполем, если 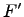 является подкольцом с единицей в кольце поля
является подкольцом с единицей в кольце поля 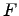 и из условия
и из условия 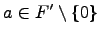 следует
следует 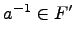 .
.
Определение. Подмножество 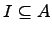 кольца
кольца  называется идеалом, если
называется идеалом, если
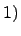
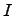 является подгруппой в аддитивной группе кольца
является подгруппой в аддитивной группе кольца  ;
;
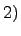 для любых
для любых 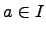 и
и 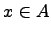 имеет место
имеет место 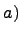
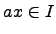 (правый идеал) или
(правый идеал) или 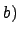
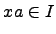 (левый идеал).
(левый идеал).
Определение. Идеал порожденный одним элементом называется главным.
Пример. 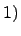 Рассмотрим кольцо
Рассмотрим кольцо 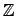 . Тогда
. Тогда 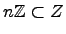 -- идеал.
-- идеал.
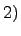 Пусть
Пусть 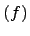 -- множество многочленов делящихся на
-- множество многочленов делящихся на 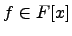 . Тогда
. Тогда 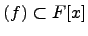 -- идеал.
-- идеал.
Утверждение. В кольце матриц 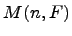 множество
множество
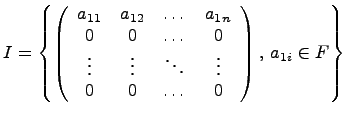
является правым идеалом и не является левым.
Теорема. Пусть 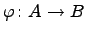 -- гомоморфизм колец. Тогда ядро
-- гомоморфизм колец. Тогда ядро 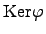 является идеалом в
является идеалом в  , а образ
, а образ 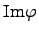 -- подкольцом в
-- подкольцом в 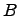 .
.
Определение. Пусть 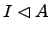 , т.е.
, т.е. 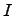 -- идеал в
-- идеал в  . Факторкольцо
. Факторкольцо 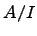 по идеалу -- это факторгруппа
по идеалу -- это факторгруппа 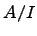 аддитивной группы кольца
аддитивной группы кольца  с операцией умножения
с операцией умножения 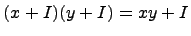 для любых
для любых 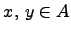 .
.
Проверим корректность умножения. Пусть 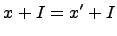 , т.е.
, т.е. 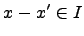 . Тогда
. Тогда 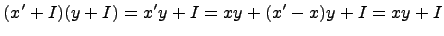 .
.
Пример. Кольцо вычетов 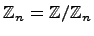 .
.
Утверждение. Если  -- алгебра с единицей над полем
-- алгебра с единицей над полем 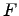 и
и 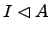 -- идеал в кольце алгебры
-- идеал в кольце алгебры  , то
, то 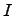 -- подпространство линейного пространства алгебры
-- подпространство линейного пространства алгебры  .
.
Пусть  -- кольцо и
-- кольцо и 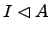 . Рассмотрим естественный гомоморфизм групп
. Рассмотрим естественный гомоморфизм групп 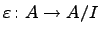 ,
, 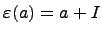 . Этот гомоморфизм является гомоморфизмом колец, так как
. Этот гомоморфизм является гомоморфизмом колец, так как 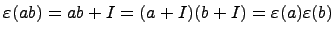 . Если
. Если  к тому же является алгеброй, то
к тому же является алгеброй, то 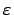 является линейным отображением и поэтому гомоморфизмом алгебр. Заметим, что
является линейным отображением и поэтому гомоморфизмом алгебр. Заметим, что 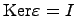 .
.
Теорема [о гомоморфизмах.] Если 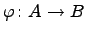 -- гомоморфизм колец, то
-- гомоморфизм колец, то 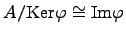 .
.
Пример. Рассмотрим эпиморфизм 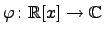 ,
, 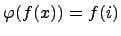 . Тогда
. Тогда 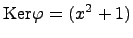 -- все многочлены делящиеся на
-- все многочлены делящиеся на 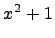 и
и 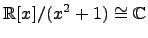 .
.
Пример. 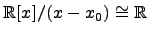 ,
, 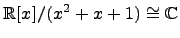 ,
, 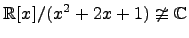 .
.
Теорема. Для всякого неприводимого над полем 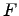 многочлена
многочлена 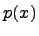 степени больше
степени больше 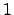 существует расширение
существует расширение 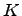 поля
поля 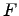 , в котором многочлен
, в котором многочлен 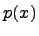 имеет корень.
имеет корень.
Определение. Простое кольцо -- это ненулевое кольцо, в котором нет идеалов кроме нулевого и всего кольца.
Утверждение. В поле нет идеалов кроме нулевого и всего поля.
Определение. Ассоциативное кольцо с единицей, в котором всякий ненулевой элемент обратим, называется телом. Алгебра, являющаяся телом, называется алгеброй с делением.
В доказательстве утверждения коммутативность не используется, то мы сразу получаем
Утверждение. Любое тело является простым кольцом.
Теорема. Кольцо (алгебра) всех матриц 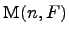 порядка
порядка 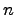 над полем
над полем 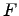 является простым.
является простым.
Определение. Рассмотрим 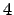 -ех мерное линейное пространство
-ех мерное линейное пространство  над
над 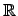 с базисом
с базисом 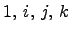 , т.е.
, т.е. 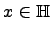 имеет вид
имеет вид 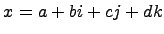 ,
, 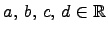 .
.
В этом пространстве  определено умножение базисных векторов
определено умножение базисных векторов 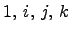 следующим образом
следующим образом 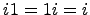 ,
, 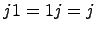 ,
, 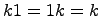 ,
, 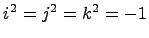 ,
, 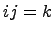 ,
, 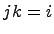 ,
, 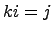 . Следовательно, определено умножение элементов
. Следовательно, определено умножение элементов 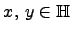 . Легко проверяется, что это умножение ассоциативно. Таким образом,
. Легко проверяется, что это умножение ассоциативно. Таким образом,  является ассоциативной
является ассоциативной 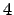 -ех мерной алгеброй над
-ех мерной алгеброй над 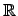 с единицей. Элемент
с единицей. Элемент 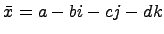 называется сопряженным к элементу
называется сопряженным к элементу 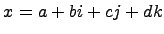 , причем
, причем 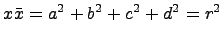 . Получаем, что каждый ненулевой элемент
. Получаем, что каждый ненулевой элемент 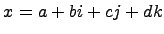 имеет обратный
имеет обратный 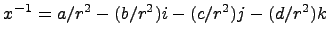 .
.
Полученная алгебра с делением  называется алгеброй кватернионов.
называется алгеброй кватернионов.
Пусть  -- конечномерная ассоциативная алгебра с
-- конечномерная ассоциативная алгебра с 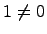 над
над 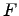 .
.
Рассмотрим отображение 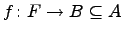 ,
, 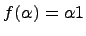 . Отображение
. Отображение 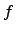 является инъективным гомоморфизмом, так как
является инъективным гомоморфизмом, так как 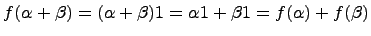 ,
, 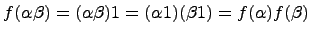 и если
и если 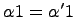 , то
, то 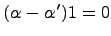 , т.е.
, т.е. 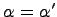 (
( 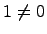 ). Таким образом
). Таким образом 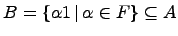 -- подалгебра (подполе) изоморфное полю
-- подалгебра (подполе) изоморфное полю 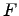 (так как ).
(так как ).
Центр 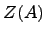 алгебры
алгебры  -- это множество
-- это множество 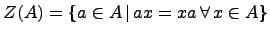 . Центр является подалгеброй (проверяется на прямую). Подалгебра
. Центр является подалгеброй (проверяется на прямую). Подалгебра 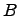 содержится в
содержится в 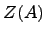 . Действительно, для любых
. Действительно, для любых 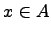 и
и 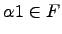 имеем
имеем 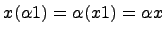 и
и 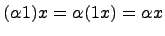 .
.
Пусть 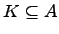 -- подполе в
-- подполе в  (
( 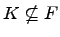 ). Тогда
). Тогда  -- (левое) линейное пространство над
-- (левое) линейное пространство над 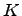 , но
, но  может не быть алгеброй над
может не быть алгеброй над 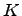 , так как может быть нарушена аксиома
, так как может быть нарушена аксиома 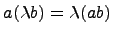 , если
, если 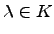 не содержится в центре
не содержится в центре 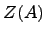 . Если
. Если  -- коммутативная алгебра, то
-- коммутативная алгебра, то  будет алгеброй над любым подполем.
будет алгеброй над любым подполем.
Пример. Имеем 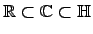 . Здесь
. Здесь  является алгеброй над
является алгеброй над 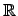 , но не является над
, но не является над 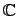 .
.
Пусть  -- конечномерная ассоциативная алгебра с
-- конечномерная ассоциативная алгебра с 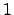 над
над 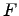 , и
, и 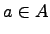 -- произвольный элемент. Рассмотрим линейный оператор
-- произвольный элемент. Рассмотрим линейный оператор 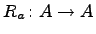 ,
, 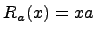 (аксиомы оператора проверяются на прямую). Оператор
(аксиомы оператора проверяются на прямую). Оператор 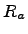 является
является 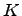 -линейным для любого подполя
-линейным для любого подполя 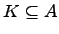 . Пусть
. Пусть 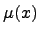 -- минимальный многочлен для линейного оператора
-- минимальный многочлен для линейного оператора 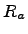 . Так
. Так 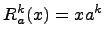 , то
, то 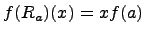 для любого многочлена
для любого многочлена 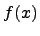 . Следовательно,
. Следовательно, 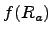 является нулевым оператором тогда и только тогда, когда
является нулевым оператором тогда и только тогда, когда 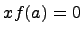 для любого
для любого 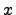 (в частности для
(в частности для 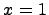 ), т.е.
), т.е. 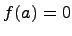 .
.
Лемма.  Если
Если  -- алгебра над
-- алгебра над 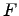 и минимальный многочлен
и минимальный многочлен 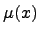 для
для 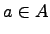 (для оператора
(для оператора 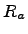 ,
, 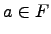 ) имеет степень
) имеет степень 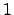 , то
, то 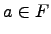 .
.
 Если
Если  -- алгебра с делением, то минимальный многочлен
-- алгебра с делением, то минимальный многочлен 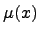 для
для 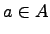 (для оператора
(для оператора 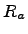 ) неприводимый над полем
) неприводимый над полем 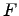 .
.
Теорема. 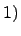 Конечномерная (коммутативная) алгебра с делением над
Конечномерная (коммутативная) алгебра с делением над 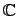 одномерна (и совпадает с
одномерна (и совпадает с 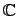 ).
).
 Конечномерная коммутативная алгебра с делением над
Конечномерная коммутативная алгебра с делением над 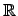 или одномерна (и совпадает с
или одномерна (и совпадает с 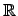 ) или двумерно (и изоморфна
) или двумерно (и изоморфна 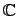 ).
).
Лемма. Пусть 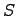 -- подмножество в алгебре
-- подмножество в алгебре  с делением над
с делением над 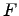 , причем элементы из
, причем элементы из 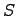 попарно перестановочны. Тогда
попарно перестановочны. Тогда 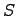 и
и 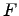 содержатся в некотором подполе
содержатся в некотором подполе 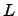 алгебры
алгебры  .
.
Теорема [Фробениус.] Всякая конечномерная алгебра с делением над 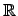 изоморфна одной из трех
изоморфна одной из трех 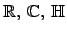 .
.
Дата добавления: 2021-09-07; просмотров: 763;











