Формулы преобразования электромагнитного поля.

Специальная теория относительности и уравнения Максвелла в трёхмерном пространстве.

Принцип относительности постулирует как обобщение экспериментальных фактов равноправие всех инерциальных систем отсчёта. Система уравнений Максвелла как основа классической электродинамики в соответствии с принципом относительности должна иметь один и тот же вид в каждой из инерциальных систем отсчёта, т.е. должна быть инвариантной относительно преобразований системы координат (и времени!) при переходе из одной инерциальной системы отсчёта в другую. Это свойство системы уравнений Максвелла действительно имеет место в специальной теории относительности, основу которой составляют преобразования Лоренца. На элементарном уровне изучения этого вопроса можно ограничиться привычными представлениями о трёхмерном евклидовом пространстве с декартовой системой пространственных координат (x,y,z) и текущем времени t, рассматривая физические величины, совокупность которых составляет электромагнитное поле, как скаляры и векторы в описанном трёхмерном пространстве, зависящие от времени. Заметим, что понятия «скаляр» и «вектор» определены при этом относительно преобразований системы пространственных координат. Поскольку составляющие электромагнитного поля зависят от координат трёхмерного пространства и времени, а при преобразованиях Лоренца координаты и время специфическим образом меняются (изменение времени связано с изменением координат), скаляры и трёхмерные векторы электромагнитного поля, естественно, должны преобразовываться к новому виду.

Формулы преобразования электромагнитного поля.

Формулы преобразования электромагнитного поля при переходе из инерциальной системы отсчёта 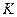в инерциальную систему отсчёта 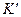с совпадающими направлениями координатных осей, движущуюся относительно исходной системы отсчёта 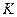со скоростью V вдоль оси х, постулируем:

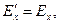
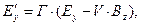
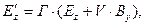
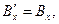
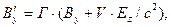
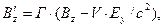(1)

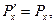
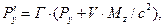
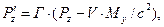
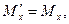
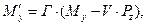
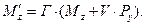
Здесь, как и ранее, символом Г обозначена величина 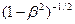, символ 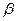обозначает отношение скорости V к скорости света с в вакууме. Величины Е, В, Р и М с нижними индексами являются соответствующими проекциями векторов напряжённости электрического поля, индукции магнитного поля, поляризованности и намагниченности среды. Штрих – верхний индекс – у проекции вектора означает, что эта величина рассматривается в системе отсчёта .

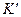Для объемной плотности заряда запишем закон преобразования в форме:

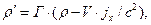(2)

а для компонент вектора объемной плотности тока -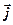

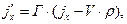
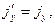
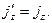(3)

Заметим, что в силу специфики преобразований Лоренца величина объёма тела 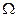не остаётся неизменной из-за сокращения продольной длины тела, параллельной направлению скорости V:

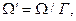(4)

поэтому при 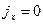из соотношения (2) следует:

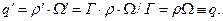(5)

Говорят, что величина электрического заряда 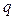является инвариантом относительно преобразований Лоренца.

Соотношений (1)-(3) достаточно, чтобы рассчитать значения всех компонент электромагнитного поля в системе отсчета .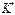

13.2.2. Инвариантность системы уравнений Максвелла относительно преобразований Лоренца. Стоит задуматься над тем фактом, что если принять как постулат соотношения (1)-(3) предыдущего раздела, то система уравнений Максвелла в “штрихованной системе” записывается в форме, идентичной форме записи системы уравнений Максвелла в нештрихованной, исходной системе отсчета. Справедливо и обратное: если инвариантность формы записи системы уравнений Максвелла требовать как условие, то при преобразовании координат и времени по Лоренцу получим соотношения (1)-(3) предыдущего раздела.

Убедимся, что система уравнений Максвелла действительно инвариантна относительно преобразований Лоренца, если справедливы обсуждаемые соотношения. Дифференциальная форма уравнений Максвелла содержит частные производные по пространственным переменным и времени. Переменные 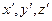и 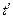можно в общем случае рассматривать как переменные, от которых зависят “исходные” координаты и время:

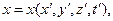
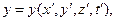
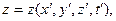
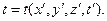(1)

В этом случае из математического анализа следует:

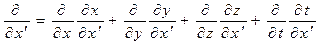(2)

и так далее. Для рассматриваемого случая из формул преобразования Лоренца следуют операторные соотношения:

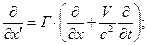
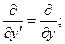
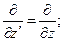
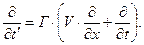(3)

Рассмотрим проекцию на ось х уравнения

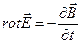
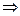
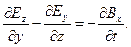(4)

Если инвариантность имеет место, то должно быть справедливым уравнение

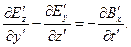(5)

Эквивалентное условие: уравнение (5) при переходе к «нештрихованным» переменным должно превращаться в уравнение (4).

В уравнении (5) используем соотношения (1) предыдущего раздела и операторные соотношения (3):

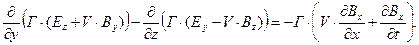(6)

Из уравнения (6) следует:

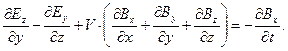(7)

Поскольку в исходной системе координат справедливо уравнение

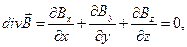(8)

приходим к уравнению (4).

Подобным образом можно убедиться в том, что при справедливости соотношений (1)-(3) предыдущего раздела система уравнений Максвелла в одной системе координат переходит в систему уравнений Максвелла во второй системе координат с сохранением формы записи.

13.2.3. Уравнения Минковского для электромагнитного поля в движущейся среде. Система уравнений Максвелла является «замкнутой» при включении в неё так называемых материальных уравнений. Для изотропной однородной среды, если она покоится в системе отсчёта 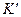, материальные уравнения имеют вид:

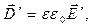
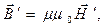
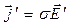. (1)

Величины относительной диэлектрической проницаемости 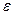, относительной магнитной проницаемости 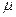и электропроводности 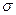изотропной среды являются скалярными величинами относительно преобразований Лоренца. При переходе в лабораторную систему отсчёта эти величины остаются постоянными, а векторы, входящие в систему материальных уравнений (1) преобразуются по известным правилам. В лабораторной системе отсчёта возникает система уравнений электромагнитного поля с учётом движения среды:

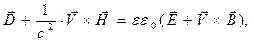(2)

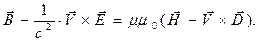(3)

Систему уравнений (2)-(3) называют уравнениями Минковского. В нерелятивистском случае 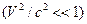уравнения (2)-(3) упрощаются:

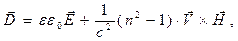(4)

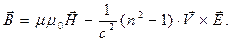(5)

Здесь 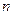- показатель преломления среды.

Закон Ома в дифференциальной форме приобретает вид

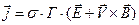(6)

в релятивистском приближении и

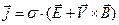(7)

в нерелятивистском случае.