Примеры практических приёмов вычислений с использованием тензорных обозначений в пространстве трёх измерений.
Используя определение 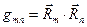 , покажем, что
, покажем, что  , т.е., что существует матрица, обратная матрице
, т.е., что существует матрица, обратная матрице 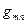 . Рассмотрим аналитическое выражение для объёма V параллелепипеда, построенного с помощью направляющих векторов
. Рассмотрим аналитическое выражение для объёма V параллелепипеда, построенного с помощью направляющих векторов 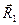 ,
, 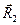 и
и 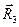 исходной системы координат:
исходной системы координат:
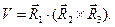 (1)
(1)
Эта величина по условию выбора координатных направлений не обращается в нуль: векторы 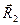 и
и 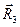 не параллельны друг другу, а вектор
не параллельны друг другу, а вектор 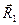 не лежит в плоскости, образованной остальными двумя направляющими векторами. Обозначим для удобства проекции направляющих векторов
не лежит в плоскости, образованной остальными двумя направляющими векторами. Обозначим для удобства проекции направляющих векторов 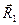 ,
, 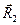 и
и 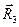 на оси декартовой системы координат как
на оси декартовой системы координат как 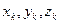 , где
, где 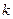 - индекс соответствующего координатного направления декартовой системы координат. В правой декартовой системе координат с безразмерными ортами координатных направлений
- индекс соответствующего координатного направления декартовой системы координат. В правой декартовой системе координат с безразмерными ортами координатных направлений 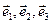 выражение для величины V приобретает вид:
выражение для величины V приобретает вид:
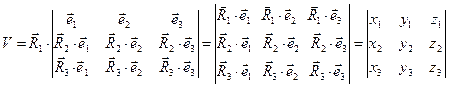 . (2)
. (2)
В соотношении (2) несколько необычно записано векторное произведение 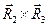 , но, очевидно, скалярное произведение направляющего вектора
, но, очевидно, скалярное произведение направляющего вектора 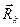 на орт
на орт 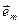 декартовой системы координат является проекцией этого направляющего вектора на выбранное координатное направление декартовой системы координат. Вычислим квадрат рассматриваемого выражения (V)2.
декартовой системы координат является проекцией этого направляющего вектора на выбранное координатное направление декартовой системы координат. Вычислим квадрат рассматриваемого выражения (V)2.
Прямое покомпонентное вычисление позволяет получить следующие результаты:
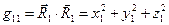 , (3)
, (3)
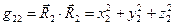 , (4)
, (4)
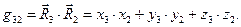 . (5)
. (5)
Для произвольных значений индексов ковариантного метрического тензора имеем
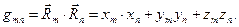 (6)
(6)
Теперь можно вычислить определитель метрического тензора в явном виде и сравнить полученный результат с результатом вычисления квадрата величины V . В итоге убеждаемся, что имеет место соотношение:
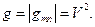
В справедливости полученного результата можно убедиться более элегантным способом. Соотношение (2) можно переписать в форме
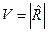 ,
, 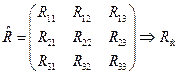 ,
,
где 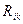 - проекция направляющего вектора
- проекция направляющего вектора 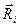 на координатную линию с ортом
на координатную линию с ортом 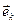 декартовой системы координат. В этих обозначениях выражение для метрического тензора
декартовой системы координат. В этих обозначениях выражение для метрического тензора 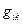 принимает вид:
принимает вид:
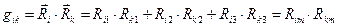 .
.
В символической форме записи (операция умножения матриц) получаем:
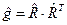 ,
,
где 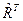 - транспонированная матрица относительно матрицы
- транспонированная матрица относительно матрицы 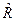 . Теперь вычислим определитель матрицы метрического тензора:
. Теперь вычислим определитель матрицы метрического тензора:
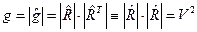 ,
,
при этом использована известная теорема линейной алгебры об умножении определителей.
Таким образом, определитель ковариантного метрического тензора отличен от нуля, матрица рассматриваемого тензора не является особенной, а тензор 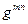 с матрицей, обратной по отношению к исходной матрице
с матрицей, обратной по отношению к исходной матрице 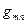 , действительно существует. Соотношения (4) и (5) раздела 13.1.3 действительно справедливы.
, действительно существует. Соотношения (4) и (5) раздела 13.1.3 действительно справедливы.
Используя «геометрическое» определение направляющих векторов взаимной системы координат, докажем соотношение 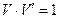 , где
, где 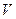 и
и 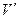 - объёмы параллелепипедов, построенных на направляющих векторах исходной и взаимной систем координат. Для объёма параллелепипеда, построенного на направляющих векторах исходной координатной системы, имеем
- объёмы параллелепипедов, построенных на направляющих векторах исходной и взаимной систем координат. Для объёма параллелепипеда, построенного на направляющих векторах исходной координатной системы, имеем
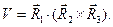 (7)
(7)
Для объёма параллелепипеда 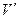 , построенного на направляющих векторах взаимной координатной системы, по аналогии запишем
, построенного на направляющих векторах взаимной координатной системы, по аналогии запишем
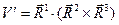 (8)
(8)
и воспользуемся определением направляющих векторов взаимной системы
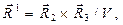
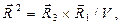
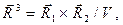 (9)
(9)
в результате имеем:
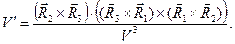 (10)
(10)
Раскрывая последовательно скобки в числителе выражения (10) с использованием известных формул векторной алгебры 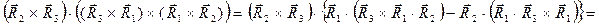
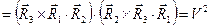 , получаем соотношение:
, получаем соотношение:
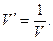 (11)
(11)
Соотношение (11), очевидно, можно было бы проверить и непосредственным вычислением. В соответствии с этим результатом убеждаемся в том, что если исходная система координат является «правой» (т.е. V>0), то взаимная система координат тоже является правой.
Используя «геометрическое» определение направляющих векторов взаимной системы координат и определение 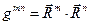 , докажем соотношение
, докажем соотношение 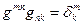 .Исходя из условия задачи, запишем последовательность выражений:
.Исходя из условия задачи, запишем последовательность выражений:
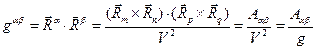 . (12)
. (12)
Здесь индексы 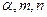 и
и 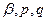 образуют соответствующие циклические перестановки индексов
образуют соответствующие циклические перестановки индексов 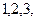 а величина квадрата объёма, построенного на направляющих векторах исходной системы координат, заменена величиной определителя матрицы ковариантного метрического тензора в соответствии с выше полученным результатом. Если удастся показать, что здесь формально введённая величина
а величина квадрата объёма, построенного на направляющих векторах исходной системы координат, заменена величиной определителя матрицы ковариантного метрического тензора в соответствии с выше полученным результатом. Если удастся показать, что здесь формально введённая величина 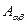 является алгебраическим дополнением соответствующего элемента матрицы ковариантного метрического тензора
является алгебраическим дополнением соответствующего элемента матрицы ковариантного метрического тензора 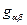 , то решение задачи можно считать законченным. Выкладки можно провести для каждой компоненты тензора
, то решение задачи можно считать законченным. Выкладки можно провести для каждой компоненты тензора 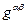 отдельно. При проведении выкладок удобно воспользоваться векторным тождеством:
отдельно. При проведении выкладок удобно воспользоваться векторным тождеством:
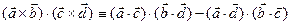 . (13)
. (13)
Так, например, для случая 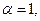
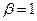 получаем:
получаем:
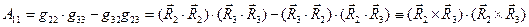 , (14)
, (14)
для случая 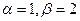 :
:
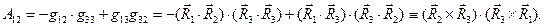 (15)
(15)
Итак, результатом решения рассматриваемой задачи является доказательство того, что матрицы контравариантного метрического тензора и ковариантного метрического тензора являются обратными по отношению друг к другу.
Используя «геометрическое» определение направляющих векторов взаимной системы координат и определение 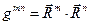 , докажем соотношение
, докажем соотношение 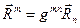 (правило поднятия индекса).Выше было доказано, что имеет место соотношение
(правило поднятия индекса).Выше было доказано, что имеет место соотношение 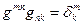 , т.е. матрицы контравариантного и ковариантного метрических тензоров являются обратными относительно друг друга. Вспомним, что направляющие векторы взаимной системы координат строились в соответствии с условиями (7) и (8) раздела 13.1.3:
, т.е. матрицы контравариантного и ковариантного метрических тензоров являются обратными относительно друг друга. Вспомним, что направляющие векторы взаимной системы координат строились в соответствии с условиями (7) и (8) раздела 13.1.3:
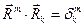 ,
, 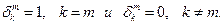 (16)
(16)
Перепишем левую часть соотношения (16) в виде:
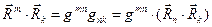
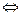
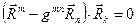 . (17)
. (17)
Поскольку условие (17) справедливо для произвольного значения индекса k, можно надеяться, что будет справедливо соотношение:
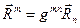 . (18)
. (18)
Строго это можно показать прямым вычислением компонент вектора 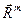 в произвольной декартовой системе координат, если последовательно вычислить левую и правую части соотношения (18) в соответствии с «геометрическими» определениями (15)),(18) и (21) раздела 13.1.3. Достаточно громоздкие выкладки удобно проделать с помощью систем символьных вычислений современных персональных компьютеров.
в произвольной декартовой системе координат, если последовательно вычислить левую и правую части соотношения (18) в соответствии с «геометрическими» определениями (15)),(18) и (21) раздела 13.1.3. Достаточно громоздкие выкладки удобно проделать с помощью систем символьных вычислений современных персональных компьютеров.
Получим ковариантные координаты точки А (рис. 3 раздела 13.1.5,) если известны её контравариантные координаты. Ограничимся анализом двумерного случая. Воспользуемся соотношением (15) раздела 13.1.3, которое, очевидно, справедливо для рассматриваемого случая. Ковариантный метрический тензор известен – соотношение (12) раздела 13.1.5:
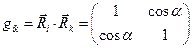 .
.
Формально получаем
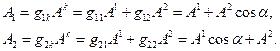 (19)
(19)
Эти же выражения непосредственно следуют из рассмотрения рис. 3 раздела 13.1.5.
В тех же предположениях получим контравариантные координаты точки А (рис.3 раздела 13.1.5), если известны её ковариантные координаты. В рамках настоящей задачи фундаментальный объект определён соотношением (12) раздела 13.1.5. Детерминант его матрицы имеет вид:
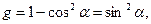 (20)
(20)
а объект 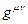 (контравариантный метрический тензор) является матрицей, обратной по отношению к матрице ковариантного метрического тензора:
(контравариантный метрический тензор) является матрицей, обратной по отношению к матрице ковариантного метрического тензора:
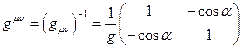 . (21)
. (21)
Формальное решение задачи получаем по формулам (15) раздела 13.1.3:
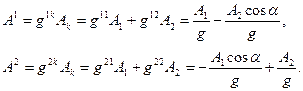 (22)
(22)
Можно ли это проверить непосредственным вычислением? Можно. Используем вспомогательную для данной задачи декартову систему координат, которая показана на рис. 3 раздела 13.1.5. Для декартовых координат рассматриваемой точки А получаем (масштаб длины в декартовой системе выбран совпадающим с масштабом длины косоугольной системы координат!):
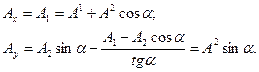 (23)
(23)
Решая систему линейных уравнений (23) относительно величин 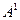 и
и 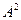 , получаем выражения (22).
, получаем выражения (22).
Покажем, что метрический тензор 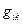 для рассмотренной выше двумерной косоугольной системы координат действительно является ковариантным тензором второго ранга относительно жёсткого поворота исходной системы координат на угол
для рассмотренной выше двумерной косоугольной системы координат действительно является ковариантным тензором второго ранга относительно жёсткого поворота исходной системы координат на угол 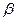 (рис.1 раздела 13.1.5).Метрический тензор
(рис.1 раздела 13.1.5).Метрический тензор 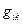 определён соотношением (5) раздела 13.1.3:
определён соотношением (5) раздела 13.1.3:
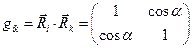 . (24)
. (24)
Матрица преобразования ковариантных компонент при переходе от одной системы координат к другой в рассматриваемом случае имеет вид:
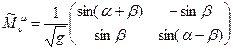 . (25)
. (25)
В соответствии с определением ковариантного тензора второго ранга мы должны получить:
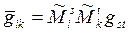 . (26)
. (26)
После выполнения всех умножений и суммирования, получаем
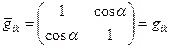 . (27)
. (27)
Полученный результат не удивителен: метрический тензор определяется «локальными» свойствами системы координат, а «новая» система координат в нашем случае идентична по своим свойствам исходной, она получена в результате «жёсткого» поворота исходной системы, метрика её при этом не должна измениться. Объект 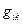 выдержал проверку, он действительно является ковариантным тензором второго ранга относительно заданного преобразования.
выдержал проверку, он действительно является ковариантным тензором второго ранга относительно заданного преобразования.
Убедиться в правильности наших рассуждений можно, если рассмотреть геометрическое содержание ковариантного метрического тензора в пространстве трёх измерений, компоненты которого выражены через коэффициенты Ламе:
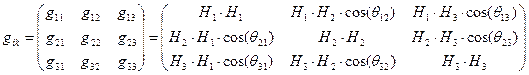 . (28)
. (28)
Физический смысл коэффициентов Ламе
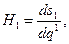
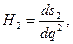
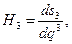 (29)
(29)
легко установить по их определению - это отношение длины элементарного отрезка вдоль координатного направления в общем случае криволинейной системы координат к элементарному приращению соответствующей криволинейной координаты, а величины 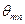 - это углы между координатными направлениями в общем случае криволинейной системы координат. Преобразование «жёсткого» поворота в рассматриваемом случае, очевидно, не должно изменять ни масштабов, ни взаимной ориентации координатных направлений системы координат: компоненты метрического тензора
- это углы между координатными направлениями в общем случае криволинейной системы координат. Преобразование «жёсткого» поворота в рассматриваемом случае, очевидно, не должно изменять ни масштабов, ни взаимной ориентации координатных направлений системы координат: компоненты метрического тензора 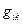 должны оставаться неизменными.
должны оставаться неизменными.
Дата добавления: 2017-09-01; просмотров: 1763;











