Формулировка классической электродинамики в четырёхмерном представлении (потенциалы, источники поля и уравнения).
Система уравнений классической электродинамики (уравнения Максвелла) может быть записана с использованием скалярного и векторного потенциалов электромагнитного поля (раздел 12.8):
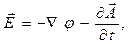
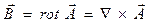 . (1)
. (1)
Для однородной изотропной среды с учётом условия калибровки Лоренца
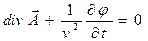 , (
, ( 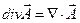 ) (2)
) (2)
справедливы неоднородные уравнения в форме Даламбера (Д`Аламбер) для скалярного и векторного потенциалов электромагнитного поля:
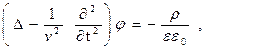 (3)
(3)
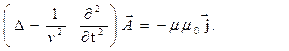 (4)
(4)
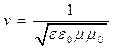 . (5)
. (5)
В уравнениях (3)-(4) правые части рассматриваются как известные функции координат и времени. Выше было показано, что уравнения (2)-(4) эквивалентны системе уравнений Максвелла.
Соотношения специальной теории относительности (СТО) приобретают наиболее простую форму в 4-пространстве – в пространстве-времени (мир Минковского). Представляется целесообразным попытаться описать основные уравнения классической электродинамики в четырёхмерном представлении. Первым шагом на этом пути может быть введение 4-потенциала и 4- плотности тока как четырёхмерных векторов относительно преобразований Лоренца в четырёхмерном пространстве-времени. В СТО можно выбрать набор координат с действительным, или мнимым временем. В предыдущем разделе было сказано, что набор координат 4-пространства с мнимым временем предпочтительнее при описании электромагнитных явлений.
Определим вектор 4-потенциала 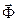 следующим образом:
следующим образом:
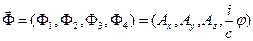 . (6)
. (6)
Определим вектор 4- плотности тока:
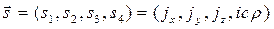 . (7)
. (7)
Напомним, что 4-радиус-вектор 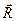 определён соотношением:
определён соотношением:
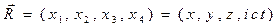 . (8)
. (8)
Для вакуума уравнения (3)-(4) можно записать единой формулой:
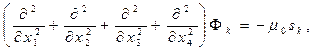
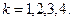 (9)
(9)
Условие калибровки Лоренца потенциалов электромагнитного поля (2) в четырёхмерном пространстве принимает вид:
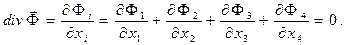 (10)
(10)
Выпишем ещё явную форму закона сохранения электрического заряда в дифференциальной форме:
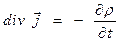
с использованием тензорных обозначений
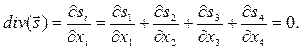 (11)
(11)
Заметим, что 4-дивергенция четырёхмерного вектора (11) является инвариантом преобразований Лоренца, т.е. скалярной величиной.
Итак, среди всех возможных решений уравнения Пуассона в 4-пространстве для каждой из проекций 4-вектора потенциала необходимо отобрать такие решения, которые удовлетворяют уравнению (10), при этом, оказывается, что источник электромагнитного поля, пропорциональный плотности 4-вектора тока должен быть согласован с условием (11). Заметим далее, что при попытке использовать введённые 4-векторы и уравнения для них в качестве исходного постулата классической электродинамики нам надо не забыть ещё и указать связь этих величин с силовыми характеристиками электромагнитного поля в трёхмерном пространстве. В чём же положительный результат проведённого анализа? Постулат о том, что 4-потенциал – это 4-вектор относительно преобразований Лоренца в пространстве-времени - сразу задаёт правило преобразования его компонент. Именно этим путём можно получить соотношения (1) предыдущего раздела.
Техника работы с четырёхмерными векторами и уравнениями классической электродинамики может быть освоена в результате разбора решения следующих задач.
Задача 1. Показать, что система уравнений (9) эквивалентна системе уравнений (3)-(4) для потенциалов электромагнитного поля в вакууме в трёхмерном пространстве.
Решение. Переписывая систему уравнений (9) в трёхмерных обозначениях, получаем
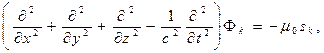
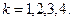 (12)
(12)
Для значений индексов k=1,2,3 эквивалентность уравнений (9) и (4) сомнений не вызывает в силу определения вектора 4-плотности тока через вектор объёмной плотности тока в трёхмерном пространстве. Для k=4 из системы уравнений (9) следует
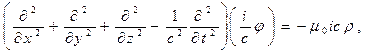 (13)
(13)
мнимая единица сокращается, а с учётом зависимости 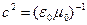 для вакуума приходим к уравнению (3).
для вакуума приходим к уравнению (3).
Задача 2. Показать, что уравнение (10) эквивалентно условию Лоренца (2) для потенциалов электромагнитного поля в вакууме в трёхмерном пространстве.
Решение. Выражение
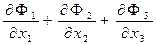 , (14)
, (14)
очевидно, эквивалентно выражению 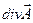 в трёхмерном пространстве. В соответствии с определением
в трёхмерном пространстве. В соответствии с определением 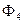 и
и 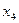 получаем:
получаем:
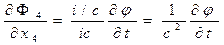 . (15)
. (15)
Действительно, обращение в нуль 4-дивергенции 4-потенциала 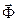 эквивалентно условию калибровки Лоренца для трёхмерных представлений потенциалов электромагнитного поля.
эквивалентно условию калибровки Лоренца для трёхмерных представлений потенциалов электромагнитного поля.
Задача 3. Показать, что уравнение (11) эквивалентно закону сохранения электрического заряда для электромагнитного поля в трёхмерном пространстве.
Решение. Выражение
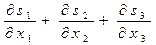 , (16)
, (16)
очевидно, эквивалентно выражению 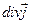 в трёхмерном пространстве. В соответствии с определением
в трёхмерном пространстве. В соответствии с определением 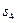 и
и 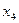 получаем:
получаем:
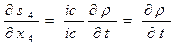 . (17)
. (17)
Действительно, обращение в нуль 4-дивергенции вектора 4- плотности тока 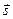 эквивалентно закону сохранения электрического заряда в трёхмерном пространстве.
эквивалентно закону сохранения электрического заряда в трёхмерном пространстве.
Задача 4. Вычислить компоненты 4-вектора 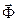 и компоненты вектора 4-плотности тока при переходе из системы координат
и компоненты вектора 4-плотности тока при переходе из системы координат 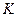 в систему координат
в систему координат 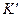 .
.
Решение. Формально решение задачи имеет вид:
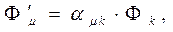
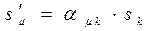 . (18)
. (18)
Матрица прямого преобразования Лоренца рассмотрена выше (соотношение (13) раздела 13.1.7):
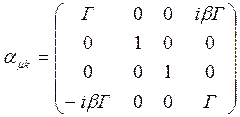 . (19)
. (19)
Осуществляя умножение матрицы 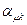 на вектор-столбцы
на вектор-столбцы 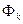 и
и 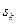 , последовательно получаем:
, последовательно получаем:
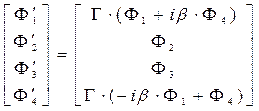 ,
, 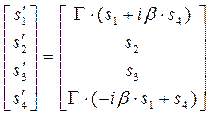 . (20)
. (20)
Отметим идентичность формы преобразования Лоренца 4-векторов разной физической природы. Если в полученных зависимостях «раскрыть» содержание символов в соответствии с принятыми выше определениями (6)-(8), получим возможность изучать преобразования векторного и скалярного потенциалов электромагнитного поля в трёхмерном пространстве и преобразования компонент плотности тока и объёмной плотности электрического заряда при переходе из системы координат 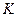 в систему координат
в систему координат 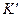 :
:
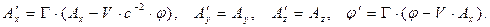 (21)
(21)
Далее естественно предположить, что в штрихованной системе координат сохраняют силу выражения для напряжённости электрического поля и индукции магнитного поля:
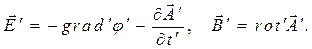 (22)
(22)
Символы grad и rot в выражениях (22) отмечены штрихами, это означает, что дифференциальные операции должны выполняться по штрихованным переменным, эти переменные являются аргументами трёхмерных векторных функций 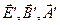 и скалярной в трёхмерном пространстве функции
и скалярной в трёхмерном пространстве функции 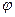 . В разделе 13.2.2 (формулы (3)) получены правила перехода от дифференцирования по штрихованным переменным к дифференцированию по координатам исходной системы отсчёта:
. В разделе 13.2.2 (формулы (3)) получены правила перехода от дифференцирования по штрихованным переменным к дифференцированию по координатам исходной системы отсчёта:
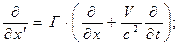
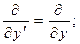
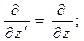
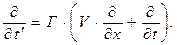 (23)
(23)
Воспользуемся соотношениями (23) для вычисления, например, формул преобразования проекции 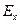 :
:
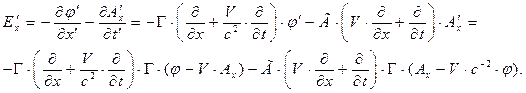
После очевидных упрощений получаем:
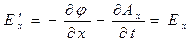 . (24)
. (24)
Для проекции 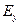 аналогичным образом получаем:
аналогичным образом получаем:
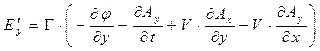 .
.
По определению в нештрихованной системе отсчёта справедливо 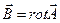 , откуда
, откуда
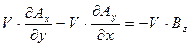 .
.
В итоге имеем формулу преобразования:
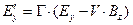 . (25)
. (25)
Предоставим читателю самостоятельно получить формулу преобразования проекции 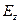 :
:
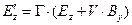 (26)
(26)
В разделе 13.2.1 мы постулировали правила преобразования электрических величин. Оказывается, что если постулировать существование 4-вектора потенциала (с соответствующими правилами преобразования) и сохранить зависимости силовых характеристик электромагнитного поля от потенциалов электромагнитного поля в трёхмерных системах координат, то первая строчка формул (1) упомянутого раздела является следствием принятого постулата.
Выведем правило преобразования, например, для проекции 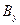 :
:
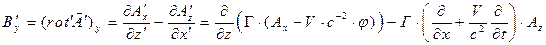 .
.
Вспоминая соотношения
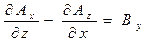 .
. 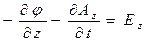
получаем окончательно:
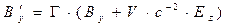 . (27)
. (27)
Аналогичным образом можно получить все выражения второй строчки формул (1) раздела 13.2.1.
Формулы преобразования вектора 4-плотности тока (20) описывают следующие правила преобразования
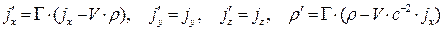 . (28)
. (28)
Легко убедиться, что соотношения (28) совпадают с формулами (2) и (3) раздела 13.2.1.
| <== предыдущая лекция | | | следующая лекция ==> |
| Формулы преобразования электромагнитного поля. | | | Тензор электромагнитного поля. |
Дата добавления: 2017-09-01; просмотров: 2157;











