Электромагнитная волна второго типа (волна Н-типа).

Рассмотрим явление распространения в волноводе электромагнитной волны второго типа. Для этой волны предполагаем выполненными условия: 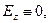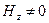.Используем эти условия для конкретизации системы уравнений (6), в результате приходим к более простой математической модели:

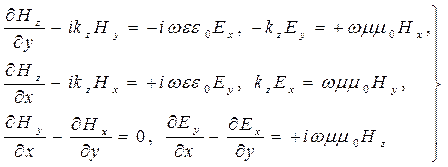(21)

Система уравнений (21) позволяет все искомыё функции, описывающие распределения физических величин по поперечному сечению волновода, выразить через зависимость 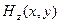, для которой можно получить уравнение Гельмгольца и сформулировать соответствующие граничные условия.

При сделанных выше предположениях из условия обращения в нуль дивергенции вектора напряжённости магнитного поля следует соотношение:

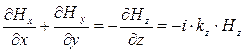. (22)

Первое уравнение системы (21) дифференцируем по переменной у , третье уравнение системы (21) дифференцируем по переменной х, результаты складываем с учётом уравнения (22) и шестого уравнения системы (21). В итоге приходим к одному линейному уравнению второго порядка в частных производных (уравнение Гельмгольца) для функции :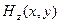

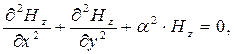
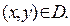(23)

Заметим, что величина параметра 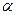в уравнении (23) совпадает с величиной параметра 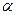в уравнении (8). Это следует из сравнения соотношений (24) и (9):

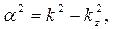
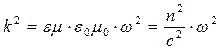. (24)

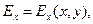
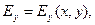
Зависимост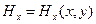и и 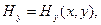замыкающие описание электромагнитной волны рассматриваемого типа, определяются выражениями

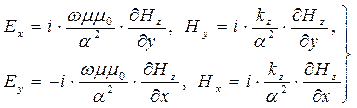(25)

Соотношения (25) являются следствием системы уравнений (21). Первое из соотношений (25), например, получается из первого уравнения системы (25), если величину 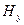исключить с помощью четвёртого уравнения системы (21) и использовать определения (24). Совокупность зависимости 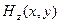и выражений (25) удовлетворяет исходным уравнениям электродинамики: условие обращения в нуль дивергенции вектора напряжённости электрического поля удовлетворяется автоматически, условие обращения в нуль дивергенции вектора напряжённости магнитного поля оказывается эквивалентным уравнению Гельмгольца для функции 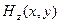, «роторные» уравнения были непосредственно использованы для получения соотношений (25). Нам остаётся проверить на непротиворечивость только систему граничных условий.

На рис. 2 показан элемент боковой поверхности волновода, направление единичного вектора нормали 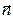к выбранному элементу поверхности, направление единичного касательного вектора 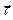, ориентация осей декартовой системы координат и ориентация «продольного» (правый нижний рисунок) и «поперечного» (правый верхний рисунок) вспомогательных контуров с выбранным положительным направлением обхода для вывода соотношений между касательными компонентами вектора напряжённости магнитного поля и компонентами вектора поверхностной плотности токов проводимости.

Анализ граничных условий начнём с рассмотрения условия непрерывности касательных компонент напряжённости электрического поля. Для рассматриваемой волны априори выполнено условие 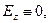поэтому достаточно потребоватьвыполнение условия обращения в нуль проекции :

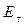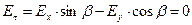на 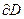. (26)

Выражая проекции вектора напряжённости электрического поля через проекцию на ось z вектора напряжённости магнитного поля по соотношениям (25), получим условие непрерывности касательных компонент напряжённости электрического поля в форме

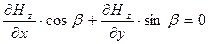на 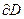. (27)

Поскольку имеет место соотношение 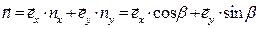, условие (27) можно записать в виде требования

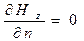на 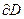. (28)

Условие непрерывности нормальных компонент вектора магнитной индукции на боковой поверхности волновода с бесконечно проводящими стенками оказывается следствием условия (28):

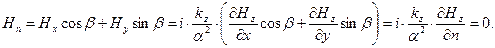(29)

Оно оказывается выполненным, если выполнено условие непрерывности касательных компонент напряжённости электрического поля.

На боковой поверхности волновода в общем случае отличны от нуля проекция на ось z вектора напряжённости магнитного поля и проекция этого же вектора на касательное направление 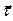. Каждая из этих проекций может формировать связанную с ней компоненту вектора поверхностной плотности токов проводимости. Рассмотрим этот вопрос более подробно.

Применяя теорему о циркуляции напряжённости магнитного поля к «продольному» вспомогательному контуру (рис.2), получаем соотношение:

Касательные компоненты вектора Н

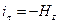на 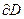. (30)

Касательная компонента вектора напряжённости магнитного поля 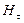может быть записана в форме:

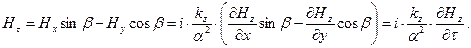(31)

Теперь теорему о циркуляции напряжённости магнитного поля применим к «поперечному» вспомогательному контуру (рис.2) и получим соотношение:

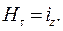(32)

С учётом предыдущего результата получаем окончательно:

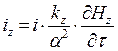(33)

Компоненты вектора поверхностной плотности тока проводимости полностью определены.

Вычислим нормальную компоненту вектора напряжённости электрического поля на боковой поверхности волновода с учётом соотношений (25) и ориентацией касательного направления к контуру поперечного сечения волновода:

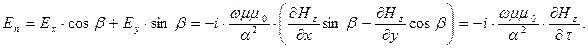(34)

С учётом определений (24) запишем выражение:

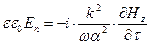. (35)

Из условий для нормальных компонент вектора 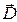на границе раздела двух сред следует выражение для поверхностной плотности стороннего электрического заряда :

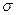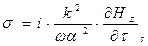. (36)

В соответствии с зависимостью (36) на боковой поверхности волновода в общем случае имеет место отличная от нуля поверхностная плотность стороннего электрического заряда. Эта физическая величина в рассматриваемой точке наблюдения изменяется с течением времени по гармоническому закону. Это изменение должно быть согласовано с распределением поверхностной плотности токов проводимости в соответствии с законом сохранения электрического заряда:

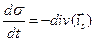. (37)

Вычислим производную по времени в уравнении (37):

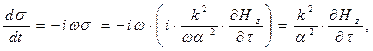(38)

Вычислим дивергенцию («расходимость») вектора поверхностной плотности токов проводимости с учётом определения операции дивергенции вектора и зависимости компонент вектора 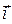от компонент вектора :

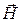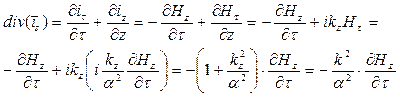. (39)

Подробные выкладки (39) преследуют цель убедить читателя в справедливости полученного результата:

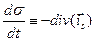. (40)

В итоге можно утверждать, что и рассматриваемая математическая постановка задачи является физически непротиворечивой.