Волны. Уравнение волны

Помимо уже рассмотренных нами движений, почти во всех областях физики встречается ещё один тип движения – волны. Отличительной особенностью этого движения, делающей его уникальным, является то, что в волне распространяются не сами частицы вещества, а изменения в их состоянии (возмущения).

Возмущения, распространяющиеся в пространстве с течением времени, называются волнами. Волны бывают механические и электромагнитные.

Упругие волны – это распространяющиеся возмущения упругой среды.

Возмущение упругой среды – это любое отклонение частиц этой среды от положения равновесия. Возмущения возникают в результате деформации среды в каком-либо её месте.

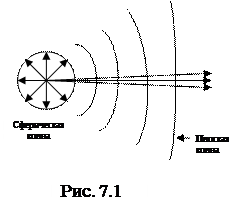
Совокупность всех точек, куда дошла волна в данный момент времени, образует поверхность, называемую фронтом волны.

По форме фронта волны делятся на сферические и плоские. Направление распространения фронта волны определяется перпендикуляром к фронту волны, называемым лучом. Для сферической волны лучи представляют собой радиально расходящийся пучок. Для плоской волны лучи- пучок параллельных прямых.

В любой механической волне одновременно существуют два вида движения: колебания частиц среды и распространения возмущения.

Волна, в которой колебания частиц среды и распространение возмущения происходят в одном направлении, называется продольной(рис.7.2 а).

Волна, в которой частицы среды колеблются перпендикулярно направлению распространения возмущений, называется поперечной(рис. 7.2 б).

В продольной волне возмущения представляют собой сжатие (или разрежение) среды, а в поперечной - смещения (сдвига) одних слоев среды относительно других. Продольные волны могут распространяться во всех средах (и в жидких, и в твёрдых, и в газообразных), а поперечные - только в твёрдых.

Каждая волна распространяется с некоторой скоростью. Под скоростью волны υ понимают скорость распространения возмущения. Скорость волны определяется свойствами среды, в которой эта волна распространяется. В твёрдых телах скорость продольных волн больше скорости поперечных.

Длиной волны λ называется расстояние, на которое распространяется волна за время, равное периоду колебания в её источнике. Поскольку скорость волны – величина постоянная (для данной среды), то пройденной волной расстояние равно произведению скорости на время её распространения. Таким образом, длина волны

λ= υТ (7. 1)

Из уравнения (7.1) следует, что частицы, отделённые друг от друга интервалом λ, колеблются в одинаковой фазе. Тогда можно дать следующее определение длины волны: длина волны есть расстояние между двумя ближайшими точками, колеблющимися в одинаковой фазе.

Выведем уравнение плоской волны, позволяющее определить смещение любой точки волны в любой момент времени. Пусть волна распространяется вдоль луча от источника с некоторой скоростью υ.

Источник возбуждает простые гармонические колебания, и смещение любой точки волны в любой момент времени определяетcz уравнением

S = Asinωt (7. 2)

Тогда точка среды, отстоящая от источника волны на расстоянии х, также будет совершать гармонические колебания, но с запаздыванием по времени на величину 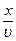, т.е. на время, необходимое для распространения колебаний от источника до этой точки. Смещение колеблющейся точки относительно положения равновесия в любой момент времени будет описываться соотношением

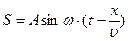(7. 3)

Это и есть уравнение плоской волны. Эта волна, характеризуется следующими параметрами:

· S — смещение от положения равновесии точки упругой среды, до которой дошло колебание;

· ω — циклическая частота колебаний, генерируемых источником, с которой колеблются и точки среды;

· υ — скорость распространения волны (фазовая скорость);

· х – расстояние до той точки среды, куда дошло колебание и смещение которой равно S;

· t – время отсчитываемое от начала колебаний;

Вводя в выражение (7. 3) длину волны λ, уравнение плоской волны можно записать так:

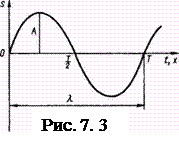
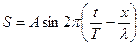(7. 4)

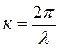или

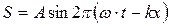(7. 5)

где 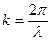называется волновым числом (число волн, приходящихся на единицу длины).

Волновое уравнение

Уравнение плоской волны (7. 5) - одно из возможных решений общего дифференциального уравнения с частными производными, описывающего процесс распространения возмущения в среде. Такое уравнение называется волновым. В уравнения (7.5) входят переменные t и х, т.е. смещение периодически меняется и во времени и в пространстве S = f(x, t). Волновое уравнение можно получить, если продифференцировать (7. 5) дважды по t:

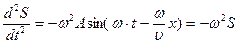
И дважды по х

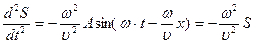
Подставляя первое уравнение во второе, получаем уравнение плоской бегущей волны вдоль оси X:

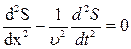(7. 6)

Уравнение (7.6) называют волновым, и для общего случая, когда смещение является функцией четырех переменных, оно имеет вид

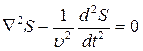(7.7)

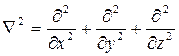, где 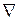—оператор Лапласа

§ 7.3 Энергия волны. Вектора Умова.

При распространении в среде плоской волны

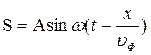(7.8)

происходит перенос энергии. Мысленно выделим элементарный объем ∆V, настолько малый, что скорость движения и деформацию во всех его точках можно считать одинаковыми и равными соответственно

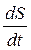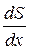и (7.9)

Выделенный объём обладает кинетической энергией

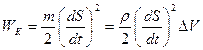(7.10)

m=ρ∆V — масса вещества в объеме ∆V, ρ — плотность среды].

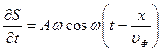(7.11)

Подставляя в (7.10) значение 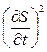, получаем

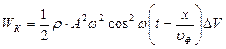(7.12)

Максимумы кинетической энергии приходятся на те точки среды, которые проходят положения равновесия в данный момент времени (S = 0), в эти моменты времени колебательное движение точек среды характеризуется наибольшей скоростью.

Рассматриваемый объем ∆V обладает также потенциальной энергией упругой деформации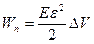

[Е — модуль Юнга; 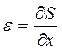— относительное удлинение или сжатие].

Учитывая формулу (7.8) и выражение для производной, находим, что потенциальная энергия равна

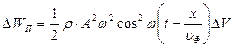(7.13)

Анализ выражений (7.12) и (7.13) показывает, что максимумы потенциальной и кинетической энергий совпадают. Следует отметить, что это является характерной особенностью бегущих волн. Чтобы определить полную энергию объема ∆V, нужно взять сумму потенциальной и кинетической энергий:

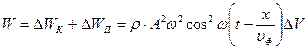(7.14)

Разделив эту энергию на объем, в котором она содержится, получим плотность энергии:

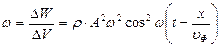(7.15)

Из выражения (7.15) следует, что плотность энергии является функцией координаты х, т. е. в различных точках пространства она имеет различные значения. Максимального значения плотность энергии достигает в тех точках пространства, где смещение равно нулю (S = 0). Средняя плотность энергии в каждой точке среды равна

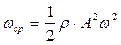(7.16)

так как среднее значение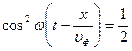

Таким образом, среда, в которой распространяется волна, обладает дополнительным запасом энергии, которая доставляется от источника колебаний в различные области среды.

Перенос энергии в волнах количественно характеризуется вектором плотности потока энергии. Этот вектор для упругих волн называют вектором Умова (по имени русского ученого Н. А. Умова). Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени сквозь единичную площадку, расположенную перпендикулярно направлению распространения волны.