Скалярный и векторный потенциалы электромагнитного поля.
Рассмотрим систему уравнений Максвелла
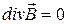 , (1)
, (1)
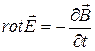 , (2)
, (2)
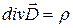 , (3)
, (3)
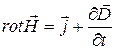 . (4)
. (4)
Заметим, что уравнения для «силовых» характеристик электромагнитного поля, т.е. для векторов 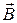 и
и 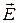 , (уравнения (1), (2)) являются однородными относительно искомых переменных. Последнее позволяет ввести «потенциалы электромагнитного поля». Целесообразность такого шага рассмотрим ниже.
, (уравнения (1), (2)) являются однородными относительно искомых переменных. Последнее позволяет ввести «потенциалы электромагнитного поля». Целесообразность такого шага рассмотрим ниже.
Рассмотрим уравнение (1). Легко видеть, что оно тождественно удовлетворяется, если положить
 , (5)
, (5)
где 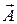 – вспомогательное векторное поле, которое назовем векторным потенциалом электромагнитного поля.
– вспомогательное векторное поле, которое назовем векторным потенциалом электромагнитного поля.
Подставим соотношение (5) в уравнение (2), поменяем порядок вычисления пространственных производных (операция 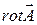 ) и производной по времени, перенесем все члены уравнения в левую часть и воспользуемся свойством линейности оператора rot, в итоге получим:
) и производной по времени, перенесем все члены уравнения в левую часть и воспользуемся свойством линейности оператора rot, в итоге получим:
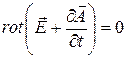 . (6)
. (6)
Полученное уравнение представляет собой локальное условие потенциальности суммарного векторного поля 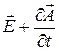 , что приводит к соотношению:
, что приводит к соотношению:
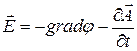 , (7) поле
, (7) поле 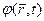 назовем скалярным потенциалом электромагнитного поля.
назовем скалярным потенциалом электромагнитного поля.
Заметим, что определения векторного (5) и скалярного (7) потенциалов электромагнитного поля по своей форме записи «неявные»: требуется подобрать такие векторное и скалярное поля, чтобы выполнялись условия (5) и (7). Обратим внимание на то обстоятельство, что с введением в рассмотрение скалярного и векторного потенциалов электромагнитного поля два из четырех уравнений Максвелла обращаются в тождество, тем самым достигается значительное упрощение системы уравнений электродинамики.
Использование скалярного (7) и векторного (5) потенциалов в уравнениях (3) и (4) исходной системы уравнений Максвелла позволяет получить систему двух связанных между собой уравнений для определения полей j и 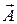 . Чтобы избежать излишней сложности, затемняющей суть вопроса, ниже рассмотрим систему уравнений Максвелла для однородной изотропной среды, для которой справедливы соотношения:
. Чтобы избежать излишней сложности, затемняющей суть вопроса, ниже рассмотрим систему уравнений Максвелла для однородной изотропной среды, для которой справедливы соотношения:
 . (8)
. (8)
Умножим каждый член уравнения (4) на величину mm0, введем эту величину под знак оператора rot в левой части уравнения, а в последнем члене правой части вынесем из-под знака производной по времени величину ee0, воспользуемся известным соотношением векторного анализа:
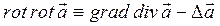 (9)
(9)
и после несложных преобразований получим:
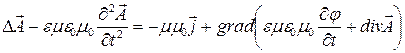 . (10)
. (10)
В уравнении (3) используем связь векторов 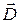 и
и 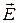 , а также, определение (7). Если вспомнить известное соотношение векторного анализа
, а также, определение (7). Если вспомнить известное соотношение векторного анализа
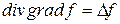 , (11)
, (11)
то после несложных преобразований будем иметь:
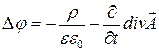 . (12)
. (12)
Значимость и практическая полезность потенциалов электромагнитного поля определяется возможностью восстановления распределений j и 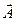 по известным распределениям в пространстве плотностей источников электромагнитного поля.
по известным распределениям в пространстве плотностей источников электромагнитного поля.
Введение понятий скалярного и векторного потенциалов электромагнитного поля привело к уменьшению числа искомых функций: вместо двух векторных (шесть компонент!) функций 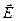 и
и 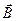 , именно к определению их может быть сведена система уравнений Максвелла, можно рассматривать одну скалярную и одну векторную функцию, т.е. всего четыре компоненты. Платой за достигнутое «упрощение» является повышение порядка системы уравнений (10) и (12) относительно потенциалов электромагнитного поля.
, именно к определению их может быть сведена система уравнений Максвелла, можно рассматривать одну скалярную и одну векторную функцию, т.е. всего четыре компоненты. Платой за достигнутое «упрощение» является повышение порядка системы уравнений (10) и (12) относительно потенциалов электромагнитного поля.
Заметим, что в пределах применимости классической электродинамики потенциалы электромагнитного поля непосредственно принципиально не наблюдаемы (в отличие от «силовых характеристик» поля).
При выводе уравнений (10) и (12) не использовались дополнительные возможности, обусловленные внутренней природой (математической структурой) потенциалов электромагнитного поля. Дело в том, что физические характеристики электромагнитного поля (и 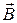 , и
, и 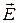 ) в соответствии с определениями (5) и (7) позволяют выбрать потенциалы некоторым удобным для данного конкретного случая образом (неоднозначность потенциалов). Такой выбор и называют калибровкой. Основная идея калибровки потенциалов электромагнитного поля состоит в том, что поля
) в соответствии с определениями (5) и (7) позволяют выбрать потенциалы некоторым удобным для данного конкретного случая образом (неоднозначность потенциалов). Такой выбор и называют калибровкой. Основная идея калибровки потенциалов электромагнитного поля состоит в том, что поля 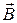 и
и 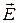 не должны изменяться при том или ином варианте выбора потенциалов
не должны изменяться при том или ином варианте выбора потенциалов 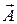 и j.
и j.
Легко проверить, что одновременная замена потенциалов электромагнитного поля
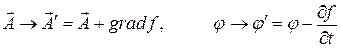 , (13)
, (13)
где 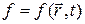 – произвольная скалярная функция, не изменяет значения векторных полей
– произвольная скалярная функция, не изменяет значения векторных полей 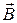 и
и 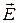 . С этой точки зрения потенциалы
. С этой точки зрения потенциалы 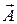 и j эквивалентны потенциалам
и j эквивалентны потенциалам 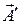 и
и 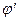 . Говорят, что физические величины
. Говорят, что физические величины 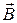 и
и 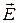 инвариантны по отношению к калибровочным преобразованиям (13). В развитие этого положения требуют, чтобы все уравнения, описывающие электромагнитное поле, обладали указанной калибровочной (или градиентной) инвариантностью. Более того, идея калибровочной инвариантности из классической электродинамики была перенесена на всю теорию поля в качестве эвристического принципа.
инвариантны по отношению к калибровочным преобразованиям (13). В развитие этого положения требуют, чтобы все уравнения, описывающие электромагнитное поле, обладали указанной калибровочной (или градиентной) инвариантностью. Более того, идея калибровочной инвариантности из классической электродинамики была перенесена на всю теорию поля в качестве эвристического принципа.
В электродинамике широко используется так называемая «лоренцева калибровка», в которой выполнено дополнительное условие
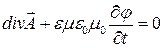 . (14)
. (14)
Это условие действительно может быть выполнено. Если взять произвольные потенциалы 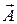 и j, применить к ним преобразование (13) и потребовать для «новых» потенциалов
и j, применить к ним преобразование (13) и потребовать для «новых» потенциалов 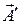 и
и 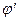 выполнения условия (14), то, оказывается, что для определения искомой функции f достаточно построить частное решение уравнения
выполнения условия (14), то, оказывается, что для определения искомой функции f достаточно построить частное решение уравнения
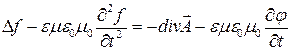 , (15)
, (15)
что вполне выполнимо, поскольку правая часть рассматриваемого уравнения является известной функцией координат и времени.
Из условия (14) следует
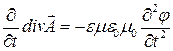 . (16)
. (16)
Легко видеть, что использование лоренцевой калибровки (14) в уравнениях (10) и (12) приводит к следующему результату:
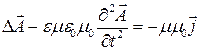 , (17)
, (17)
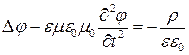 . (18)
. (18)
Если ввести в рассмотрение оператор Даламбера
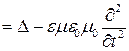 , (19)
, (19)
обычно используемый при описании волновых явлений, то уравнения (17) и (18) можно представить в очень компактной форме
ÿ 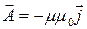 , (20)
, (20)
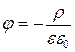 . (21)
. (21)
Лоренцева калибровка потенциалов электромагнитного поля оставляет возможным наложить на выбор потенциалов еще одно дополнительное условие. Можно, например, в дополнение к условию лоренцевой калибровки (14) потребовать выполнения условия:
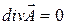 , (22)
, (22)
что эквивалентно условию 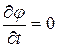 , т.е.
, т.е. 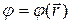 с точностью до произвольной постоянной.
с точностью до произвольной постоянной.
Если векторный и скалярный потенциалы электромагнитного поля удовлетворяют условиям (14) и (22), то говорят о «кулоновской» (или поперечной) калибровке. Выбор термина «кулоновская калибровка» определяется тем, что при этом уравнение (21) приобретает вид:
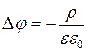 . (23)
. (23)
Это уравнение Пуассона для скалярного потенциала j – основное уравнение для одного из разделов электродинамики, раздела «электростатика», в котором кулоновское взаимодействие играет центральную роль. В силу того, что 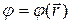 , правая часть уравнения (23) тоже должна быть функцией только пространственных координат:
, правая часть уравнения (23) тоже должна быть функцией только пространственных координат: 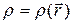 .
.
Как можно убедиться, цепочка следствий из предположения (22) достаточно велика и следствия весьма нетривиальны.
Подведем некоторые итоги.
Во-первых, заметим, что уравнения (20) и (21) не полностью эквивалентны системе уравнений Максвелла, но по внешнему виду проще: формально их можно рассматривать раздельно, структура их решений одинакова в силу того, что структура уравнений идентична. В учебной и научной литературе по электродинамике этому обстоятельству придается большое значение. Вместе с тем заметим, что раздельное, независимое рассмотрение уравнений (20) и (21) приводит к более широкому набору возможных решений, чем это допускает система уравнений Максвелла. В качестве примера можно рассмотреть вопрос о плоских электромагнитных волнах в вакууме. Система уравнений Максвелла для непроводящей изотропной среды позволяет выявить такие свойства электромагнитной волны как поперечность, взаимную ортогональность векторов напряженности электрического поля 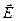 и напряженности магнитного поля
и напряженности магнитного поля 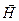 , совпадение фаз процессов колебаний в рассматриваемой точке пространства и т.д. В то же время система уравнений (20) и (21) позволяет только сделать вывод о том, что распространение возмущений скалярного поля j и векторного поля
, совпадение фаз процессов колебаний в рассматриваемой точке пространства и т.д. В то же время система уравнений (20) и (21) позволяет только сделать вывод о том, что распространение возмущений скалярного поля j и векторного поля 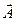 происходит с одинаковой фазовой скоростью. Но если к анализу привлечь ещё и условие лоренцевой калибровки (14), то можно получить все результаты электродинамики в отношении рассматриваемого типа волн.
происходит с одинаковой фазовой скоростью. Но если к анализу привлечь ещё и условие лоренцевой калибровки (14), то можно получить все результаты электродинамики в отношении рассматриваемого типа волн.
Во-вторых, структура уравнений, описывающих потенциалы электромагнитного поля 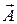 и j в форме (20) – (21) с очевидностью выявляет волновую природу электромагнитного поля, что подтверждает выполнение принципа близкодействия как основы электродинамики. Возможность нетривиальных решений уравнений (20)-(21) для вакуума позволяет говорить о физической реальности электромагнитного поля.
и j в форме (20) – (21) с очевидностью выявляет волновую природу электромагнитного поля, что подтверждает выполнение принципа близкодействия как основы электродинамики. Возможность нетривиальных решений уравнений (20)-(21) для вакуума позволяет говорить о физической реальности электромагнитного поля.
В-третьих, форма записи уравнений (20) и (21) для потенциалов наглядно выявляет объёмные источники соответствующих полей - 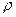 и
и 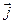 , т.е. объёмную плотность электрического заряда и объёмную плотность тока проводимости.
, т.е. объёмную плотность электрического заряда и объёмную плотность тока проводимости.
В-четвертых, определенная законченность и симметрия формы уравнений (20)-(21) не могут не рождать чувства эстетического удовлетворения.
Замечание. Все рассуждения настоящего раздела не затрагивали так называемых граничных условий, постановка которых необходима при описании электромагнитного поля в ограниченной области пространства (в безграничной области чаще всего подразумевается, что эти условия «на бесконечности» однородные). В реальных ситуациях дополнительно оказывается, что решения «независимых» между собой уравнений (20) – (21) взаимосвязаны из-за того, что граничные условия являются «комбинированными»: они, как правило, содержат и 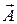 , и j (и, возможно, их производные). Последнее затрудняет решение практической задачи нахождения полей
, и j (и, возможно, их производные). Последнее затрудняет решение практической задачи нахождения полей 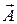 и j, следовательно, и полей
и j, следовательно, и полей 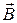 и
и 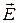 .
.
В заключение раздела ещё раз подчеркнем важность требования калибровочной инвариантности системы уравнений для потенциалов электромагнитного поля и то обстоятельство, что условие лоренцевой калибровки является полноправной обязательной частью системы уравнений классической электродинамики, записанной для потенциалов электромагнитного поля.
Дата добавления: 2017-09-01; просмотров: 2657;











