Метод Херста. Показатель Херста. Связь между нормированным размахом и фрактальной размерностью сигнала.

Метод Херста или метод нормированного размаха

Часто на практике изучаемые системы (от солнечных пятен, среднегодовых значений выпадения осадков и до финансовых рынков, временных рядов экономических показателей) не являются нормально-распределенными или близкими к ней. Для анализа таких систем Херстом был предложен метод Нормированного размаха (RS-анализ). Главным образом данный метод позволяет различить случайный и фрактальный временные ряды, а также делать выводы о наличии непериодических циклов, долговременной памяти и т.д.

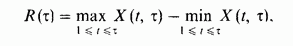
R- размах

Херст использовал безразмерное отношение R/S, где S- стандартное отклонение, то есть квадратный корень из дисперсии.

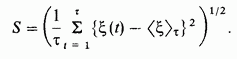
Показатель степени Хёрста, показатель Хёрста или коэффициент Хёрста — мера, используемая в анализе временных рядов. Эта величина уменьшается, когда задержка между двумя одинаковыми парами значений во временном ряду увеличивается.

Решение уравнения Херста может быть целочисленным и дробным(положительное), в частном случае оно равно 0.

Если 0<H<=1/2 – то сигналы случайные(чем ближе к 1/2 тем меньше шумовой компоненты)

Если H> 1/2 – сигнал детерминированный

В радиоэлектронике метод Херста применяется в расчетах набега фазы (изменение фазы относительно начального), а также для описания ухода частоты.

Через показатель Херста можно определить фрактальную размерность.

Если 0<H<=1/2 то D=1/H

Если H> 1/2 то D=2-H