Модели случайных процессов

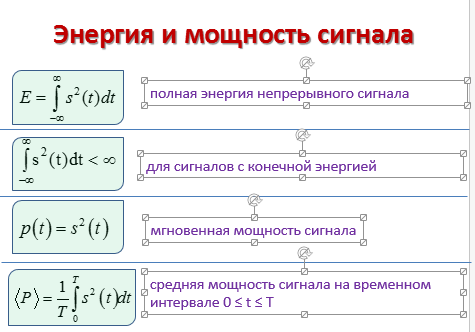
Раскройте смысл понятия «Сигнал». Опишите классификацию сигналов. Энергия и мощность сигналов. Перечислите задачи и применение цифровой обработки сигналов. Опишите методы, использующиеся для цифровой обработки сигналов.

Сигнал можно рассматривать как зависимость одной величины от другой.

Таким образом, математически сигналы представляют собой функцию одной или нескольких независимых переменных.

Сигнал является носителем информации.

Виды сигналов:

Одномерные двумерные

Непрерывные дискретные

Периодические непериодические

Импульсные затухающие

Аналоговые цифровые

Детерминированные случайные.

Задачи и применение ЦОС

• Цифровая обработка сигналов (ЦОС) — преобразование сигналов, представленных в цифровой форме.

• Любой непрерывный (аналоговый) сигнал s(t) может быть подвергнут дискретизации по времени и квантованию по уровню (оцифровке), то есть представлен в цифровой форме.

• Существуют методы обработки сигналов во временной и частотной областях.

ПРИМЕНЕНИЕ ЦОС

• сжатие (компрессия) сигналов

• обработка звуковых сигналов

• распознавание образов

• обработка изображений

• фильтрация сигналов

• обработка сейсмологических данных

• многоскоростная обработка сигналов

• составление прогноза погоды.

Методы:ипользующиеся в ЦОС.

• фрактальный и мультифрактальный анализ сигналов

• корреляционный анализ сигналов

• Фурье-анализ периодических и непериодических сигналов

• вейвлет-анализ сигналов

• информационно-энтропийный анализ сигналов

• фильтрация сигналов

• сжатие (компрессия) сигналов

• распознавание образов.

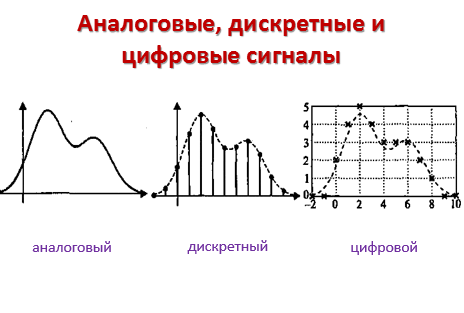
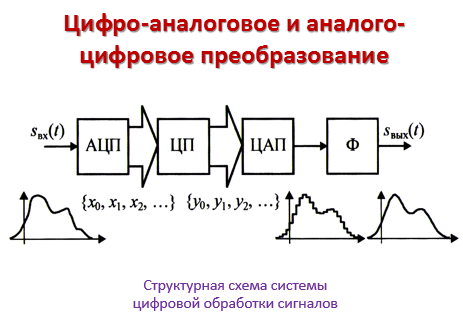
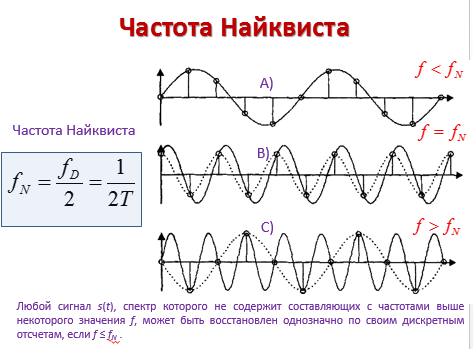
Опишите смысл понятий «аналоговый сигнал», «дискретный сигнал» и «цифровой сигнал». Цифро-аналоговое и аналого-цифровое преобразование. Запишите формулу для вычисления частоты Найквиста. Сформулируйте теорему Найквиста.

Опишите смысл понятий «случайный сигнал» и «ансамбль реализаций». Опишите модели случайных процессов. Перечислите вероятностные характеристики случайных процессов. Раскройте смысл понятий «функция распределения вероятности» и «одномерная плотность вероятности».

Случайные сигналы — сигналы, мгновенные значения которых (в отличие от детерминированных сигналов) не известны, а могут быть лишь предсказаны с некоторой вероятностью, меньшей единицы. Характеристики таких сигналовявляются статистическими, то есть имеют вероятностный вид. Математическая модель изменяющегося во времени случайного сигнала называется случайным процессом.

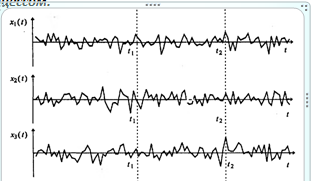Реализации случайных процессов

Модели случайных процессов

Гармонический сигнал со случайной начальной фазой

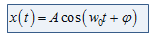Плотность вероятности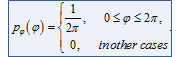

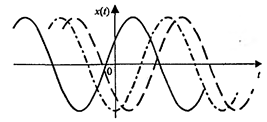
Случайный телеграфный сигнал – это случайный процесс, реализации которого принимают значения +1 и -1, причем перепады уровня происходят в случайные моменты времени и число N перепадов уровня, происходящих за время , является случайной величиной с дискретным распределением вероятности, описываемым законом Пуассона:

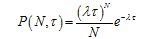
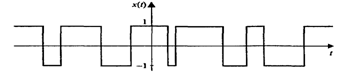Реализация случайного телеграфного сигнала