Решение уравнения методом Рунге-Кутта
Приведем сначала удобную схему вычислений по методу Рунге-Кутта, сведя ее в табл.4, и опишем порядок заполнения этой таблицы.
Схема метода Рунге-Кутта:
Таблица 4
| i | x | у | K=hf(x,y) | Δу |
| х0 | у0 | K1(0) | K1(0) | |
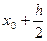
| 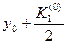
| K2 (0) | 2K2 (0) | |
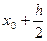
| 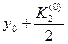
| K3(0) | 2K3(0) | |
| х0+ h | у0+ K3(0) | K4(0) | K4(0) | |
| Δу0 | ||||
| х1 | у1 |
Порядок заполнения таблицы
1. Записываем в первой строке таблицы данные значения х0,у0.
2. Вычисляем f (х0,у0), умножаем на h и заносим в таблицу в качестве K1(0).
3. Записываем во второй строке таблицы 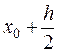 ,
, 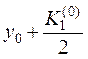 .
.
4. Вычисляем 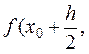
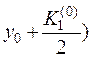 , умножаем на h и заносим в таблицу в качестве K2 (0).
, умножаем на h и заносим в таблицу в качестве K2 (0).
5. Записываем в третьей строке таблицы 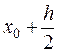 ,
, 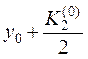 .
.
6. Вычисляем 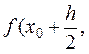
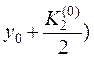 , умножаем на h и заносим в таблицу в качестве K3(0).
, умножаем на h и заносим в таблицу в качестве K3(0).
7. Записываем в четвертой строке таблицы х0 + h, у0 + K3(0).
8. Вычисляем 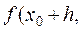
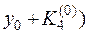 , умножаем на h и заносим в таблицу в качестве K4(0).
, умножаем на h и заносим в таблицу в качестве K4(0).
9. В столбец Δу записываем числа K1(0), 2K2 (0), 2K3(0), K4(0).
10. Суммируем числа, стоящие в столбце Δу, делим на 6 и заносим в таблицу в качестве Δу0.
11. Вычисляем у1 = у0 + Δу0.
Затем все вычисления повторяются в том же порядке, принимая за начальную точку (х1, у1). Заметим, что если f(x,y) являются достаточно сложной функцией, то рекомендуется вычисление правой части дифференциального уравнения включать в табл.4 или, если эти вычисления громоздки, записывать их в отдельную таблицу.
Итак, решим исходное уравнение методом Рунге-Кутта. Приближенные значения у1, у2,..,у5решения этого уравнения будем вычислять по формулам (10.14)–( 10.16), где 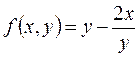 , в порядке, указанном в приведенной выше схеме. Результаты вычислений помещаем в табл.5, заполняя ее в указанном выше порядке.
, в порядке, указанном в приведенной выше схеме. Результаты вычислений помещаем в табл.5, заполняя ее в указанном выше порядке.
При i = 0.
1. Записываем в первой строке х0 = 0,0, у0 = 1,0000.
2. Вычисляем f (х0,у0) = 1,0000; тогда K1(0) = 0,2 ∙1,0000 = 0,2000.
3. Записываем во второй строке 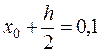 ,
, 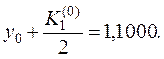
4. Вычисляем 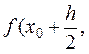
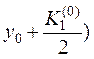 = 0,9182; тогда K2 (0) = 0,1836.
= 0,9182; тогда K2 (0) = 0,1836.
5. Записываем в третьей строке 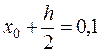 ,
, 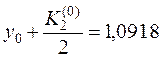 .
.
6. Вычисляем 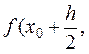
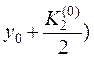 = 0,9086; тогда K3(0) = 0,1817.
= 0,9086; тогда K3(0) = 0,1817.
7. Записываем в четвертой строке х0 + h = 0,2; у0 + K3(0) = 1,1817.
8. Вычисляем f(х0+ h, у0+ K3(0)) = 0,8432; тогда K4(0) = 0,1686.
9. В столбец Δу записываем числа K1(0), 2K2 (0), 2K3(0), K4(0).
10. Вычисляем 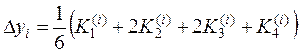 = 0,1832.
= 0,1832.
11. Получаем у1 = у0 + Δу0 = 1,1832.
Таблица 5
| i | x | у | K=hf(x,y) | Δу |
| 0,0 | 1,0000 | 0,2000 | 0,2000 | |
| 0,1 | 1,1000 | 0,1836 | 0,3672 | |
| 0,1 | 1,0918 | 0,1817 | 0,3624 | |
| 0,2 | 1,1817 | 0,1686 | 0,1686 | |
| 0,1832 | ||||
| 0,2 | 1,1832 | 0,1690 | 0,1690 | |
| 0,3 | 1,2677 | 0,1588 | 0,3178 | |
| 0,3 | 1,2627 | 0,1575 | 0,3150 | |
| 0,4 | 1,3407 | 0,1488 | 0,1488 | |
| 0,1584 | ||||
| 0,4 | 1,3417 | 0,1490 | 0,1490 | |
| 0,5 | 1,4162 | 0,1420 | 0,2840 | |
| 0,5 | 1,4127 | 0,1409 | 0,2819 | |
| 0,6 | 1,4826 | 0,1346 | 0,1346 | |
| 0,1416 | ||||
| 0,6 | 1,4833 | 0,1348 | 0,1348 | |
| 0,7 | 1,5507 | 0,1296 | 0,2592 | |
| 0,7 | 1,5481 | 0,1287 | 0,2575 | |
| 0,8 | 1,6120 | 0,1239 | 0,1239 | |
| 0,1292 | ||||
| 0,8 | 1,6125 | 0,1241 | 0,1241 | |
| 0,9 | 1,6745 | 0,1199 | 0,2398 | |
| 0,9 | 1,6725 | 0,1192 | 0,2385 | |
| 1,0 | 1,7317 | 0,1154 | 0,1154 | |
| 0,1196 | ||||
| 1,0 | 1,7321 |
Значения х1 = 0,1, у1 = 1,1832 заносим в строку, помеченную индексом i = 1, и снова проводим вычисления по формулам (10.14)–( 10.16).
Дата добавления: 2021-09-07; просмотров: 548;











