Контрольная работа №8
Пусть дано:
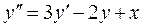 ; у(0) = у'(0) = 1; [0;0,3]; h = 0,1.
; у(0) = у'(0) = 1; [0;0,3]; h = 0,1.
Решение дифференциального уравнения методом Рунге-Кутта
С помощью подстановки у' = z, у'' = z' заменим исходное дифференциальное уравнение системой уравнений:
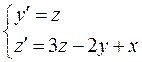 (**)
(**)
с начальными условиями у(0) = 1, z(0) = 1. Таким образом,
f1(x, y, z)= z,
f2(x, y, z)= 3z –2y + x .
Шагом интегрирования h = 0,1 разобьем отрезок [0;0,3] на три равных части точками х0= 0, х1= 0,1, х2 = 0,2, х3 = 0,3. Для вычисления приближенных значений у1, у2, у3 и z1, z2, z3 решения системы (**) воспользуемся формулами (10.17). Результаты вычислений помещены в табл.11. Заполнение таблицы ведется в следующем порядке.
При i = 0:
1. Записываем в первой строке х0 = 0, у0 = 1, z0 = 1.
2. Вычисляем f1(x0, y0, z0)= z0 = 1, f2(x0, y0, z0) = 3z0 –2y0 + x0 = 1,
тогда К1(0) = 0,1∙1 = 0,1; l1(0) = 0,1∙1 = 0,1.
3. Записываем во второй строке
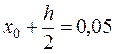 ,
, 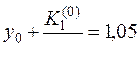 ,
, 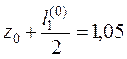 .
.
4. Вычисляем 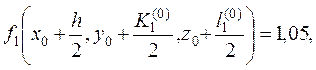
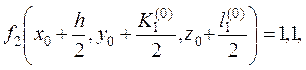
тогда 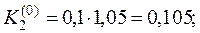
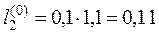 .
.
5. Записываем в третьей строке
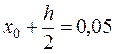 ,
, 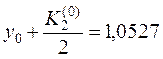 ,
, 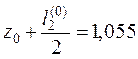 .
.
6. Вычисляем
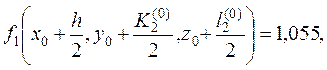
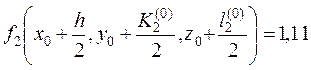 ,
,
тогда 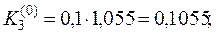
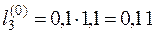 .
.
7. Записываем в четвертой строке
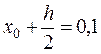 ,
, 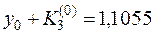 ,
, 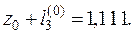
8. Вычисляем
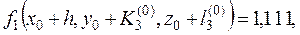
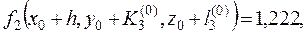
тогда 
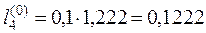 .
.
9. В столбцы  и
и  записываем числа K1(0), 2K2(0), 2K3(0), K4(0) и
записываем числа K1(0), 2K2(0), 2K3(0), K4(0) и  соответственно.
соответственно.
10. Вычислим

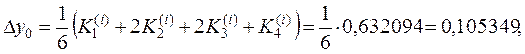
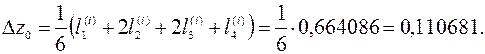
11. Получаем 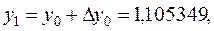
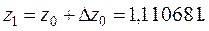
Значения 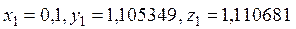 заносим в строку, помеченную индексом i = 1, и снова проводим вычисления по формулам (10.17). В результате этих вычислений получаем следующую таблицу приближенных значений решения системы (**).
заносим в строку, помеченную индексом i = 1, и снова проводим вычисления по формулам (10.17). В результате этих вычислений получаем следующую таблицу приближенных значений решения системы (**).
Таблица 11
| i | x | y | z | K | l | Δy | Δz |
| 1,000000 | 1,000000 | 0,100000 | 0,100000 | 0,100000 | 0,100000 | ||
| 0,05 | 1,050000 | 1,050000 | 0,105000 | 0,110000 | 0,210000 | 0,220000 | |
| 0,05 | 1,052750 | 1,055000 | 0,105500 | 0,111000 | 0,211000 | 0,222000 | |
| 0,1 | 1,105500 | 1,111000 | 0,111100 | 0,122200 | 0,111100 | 0,122200 | |
| 0,105349 | 0,110681 | ||||||
| 0,1 | 1,105349 | 1,110681 | 0,111069 | 0,122134 | 0,111068 | 0,122134 | |
| 0,15 | 1,160883 | 1,171748 | 0,1171748 | 0,134348 | 0,234349 | 0,268696 | |
| 0,15 | 1,163936 | 1,1778546 | 0,117785 | 0,135557 | 0,235570 | 0,471140 | |
| 0,2 | 1,223134 | 1,246250 | 0,124625 | 0,149248 | 0,124625 | 0,149248 | |
| 0,117602 | 0,1351985 | ||||||
| 0,2 | 1,222951 | 1,245879 | 0,124588 | 0,149174 | 0,124588 | 0,149174 | |
| 0,25 | 1,285245 | 1,320466 | 0,1320466 | 0,164091 | 0,264093 | 0,328182 | |
| 0,25 | 1,288974 | 1,327925 | 0,1327925 | 0,1655825 | 0,265585 | 0,331165 | |
| 0,3 | 1,355743 | 1,411462 | 0,411462 | 0,1822899 | 0,1411462 | 0,1822899 | |
| 0,1325686 | 0,165135 | ||||||
| 0,3 | 1,3555196 | 1,4110142 |
| i | xi | yi | zi |
| 0,1 | 1,105349 | 1,110681 | |
| 0,2 | 1,222951 | 1,245879 | |
| 0,3 | 1,3555196 | 1,4110142 |
Дата добавления: 2021-09-07; просмотров: 498;











