Контрольная работа № 6
Пусть дано:
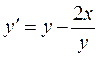 ; у(0)=1; x
; у(0)=1; x 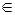 [1,2] .
[1,2] .
Шагом интегрирования h = 0,2 отрезок [0,1] разбивается на пять равных частей точками х0 = 0, х1 = 0,2, х2 = 0,4, х3 = 0,6, х4 = 0,8, х5 = 1,0.
Решение уравнения методом Эйлера
Приближенные значения у1, у2,..,у5решения исходного уравнения в точках х1, х2,… х5 вычислим по формуле (10..8), в которой 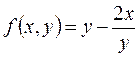 . Результаты вычисления будем заносить в табл.2. Заполняется она следующим образом.
. Результаты вычисления будем заносить в табл.2. Заполняется она следующим образом.
В первой строке при i = 0 записываются начальные значения х0 = 0,0; у0 = 1,0000и по ним вычисляются f(х0, у0) = 1,0000, а затем Δу = hf (х0, у0) = = 0,2*1,0000 = 0,2000. Тогда по формуле (108) при i = 0 находим у1 = у0 + Δу0 = = 1,0000 + 0,2000 = 1,2000.
Во второй строке при i = 1 записываем значения х1 = 0,2; у1 = 1,2000. Используя их, вычислим f (х1,у1)= 0,8667 затем
Δу1 = hf (х1, у1)= 0,2*0,8667 = 0,1733.
И по формуле (108) при i = 1 получаем у2 = у1+Δу1 = 1,2000 + 0,1733 = 1,3733. При i = 2, 3, 4, 5 вычисления ведутся аналогично.
Таблица 2
| i | х1 | у1 | Вычисление (х1,у1) | Δу1 | |
| 2х1/у1 | у1–2х1/у1 | ||||
| 0,0 | 1,0000 | 1,0000 | 0,2000 | ||
| 0,2 | 1,2000 | 0,3333 | 0,8667 | 0,1733 | |
| 0,4 | 1,3733 | 0,5928 | 0,7805 | 0,1561 | |
| 0,6 | 1,5294 | 0,7846 | 0,7458 | 0,1492 | |
| 0,8 | 1,6786 | 0,9532 | 0,7254 | 0,1451 | |
| 1,0 | 1,8237 |
Решение уравнения модифицированным методом Эйлера
Приближенные значения у1, у2,..,у5решения исходного уравнения в точках х1, х2,… х5 вычислим по формулам (10.11) и (10.12), в которых 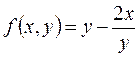 . Результаты вычислений будем заносить в табл.3. Заполняется она следующим образом.
. Результаты вычислений будем заносить в табл.3. Заполняется она следующим образом.
Таблица 3
| i | х1 | у1 | 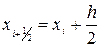
| 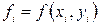
| 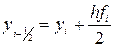
| 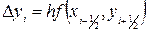
|
| 0,0 | 1,0000 | 0,1 | 1,0000 | 1,0000 | 0,1836 | |
| 0,2 | 1,1836 | 0,3 | 0,8457 | 1,2682 | 0,1590 | |
| 0,4 | 1,3426 | 0,5 | 0,7467 | 1,4173 | 0,1424 | |
| 0,6 | 1,4850 | 0,7 | 0,6769 | 1,5527 | 0,1302 | |
| 0,8 | 1,6152 | 0,9 | 0,6246 | 1,6778 | 0,1210 | |
| 1,0 | 1,7362 |
В первой строке записываем i = 0, x0 = 0,0, y0 = 1,0000. Вычисляем
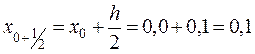 ;
; 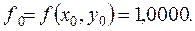
Далее находим
 ;
;
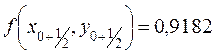
и
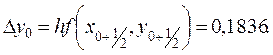
Тогда по формуле (10.12) при i = 0 имеем
у1 = у0 + Δу0 = 1,0000 + 0,1836 = 1,1836.
Используя этот результат, записываем во второй строке i = 1, x1 = 0,2, y1 = 1,1836 и последовательно находим
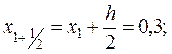
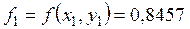 ;
;
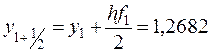 ;
; 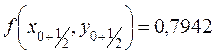 ;
;
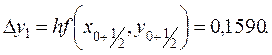
Тогда по формуле (10.12) при i = 1 имеем
у2 = у1 + Δу1 = 1,1836 + 0,1590 = 1,3426.
Заполнение таблицы при i = 2, 3, 4, 5 проводится аналогично.
Дата добавления: 2021-09-07; просмотров: 465;











