Аналитические решения заданного уравнения

Дано

у'' – 3у' + 2у =х, у(0) = у'(0) = 1. (***)

Это линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Найдем общее решение у_он этого уравнения, которое равно сумме какого-либо частного решения у_чн неоднородного уравнения и общего решения у_∞ соответствующего однородного уравнения

у_он = у_∞ + у_чн.

Запишем соответствующее однородное уравнение

у'' – 3у' + 2у = 0,

его характеристическое уравнение k² – 3k + 2 = 0 имеет корни k₁ = 2, k₂ = 1. Поэтому

у_∞ = с₁е^2х + с₂е^2х.

Для определения частного решения неоднородного уравнения (***) воспользуемся методом неопределенных коэффициентов. Так как правая часть уравнения (***) является многочленом первой степени и число ά + β_i = 0 не является корнем характеристического уравнения, то частное решение имеет вид:

у_чн =Ах +В.

Чтобы определить значения коэффициентов А и В, находим производные

у_чн = А, у_чн = 0,

подставляем у_чн, у_чн, у_чн в уравнение (19)

-3А +2Ах + 2В = х

и, сравнивая коэффициенты при одинаковых степенях х, получаем систему

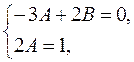
из которой находим 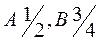. Следовательно, 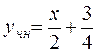и

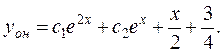
Найдем частное решение, удовлетворяющее заданным начальным условиям, для чего продифференцируем общее решение и подставим начальные условия в общее решение и его производную, в результате получим систему

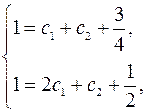
решая которую, найдем 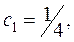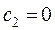.Таким образом, получили аналитическое решение заданного уравнения, удовлетворяющего данным начальным условиям

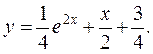
3. Сравним значения точного и приближенного решений заданного уравнения в точках х₁, х₂, х₃. Это сравнение дано в табл.12.

Таблица 12

i	yi по методу Рунге-Кутта	у(хi) – точное решение	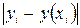- абсолютная погрешность
	1,0000000	1,000000
	1,105349	1,105351	2∙10-6
	1,222951	1,222955	4∙10-6
	1,3555196	1,3555301	1∙10-5