Контрольная работа № 5
Вычислить значение интеграла
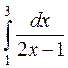 ,
, 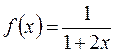 , а = 0, b = 0,
, а = 0, b = 0, 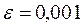 .
.
Выберем формулу для приближенного вычисления заданного определенного интеграла. Для чего найдем по формулам (9.4), (9.6), (9.10) число n точек разбиения отрезка [0,1] на частичные, которые обеспечат требуемую точность при вычислении по формулам прямоугольников, трапеций и парабол соответственно. А затем остановимся на той из приближенных формул, для которой число n будет наименьшим.
Чтобы воспользоваться формулами (9.4), (9.6), (9.10), вычислим и оценим первую, вторую и четвертую производные подынтегральной функции 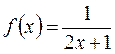 на отрезке [0,1]:
на отрезке [0,1]:
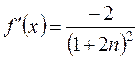 ,
, 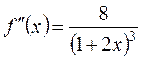 ,
,
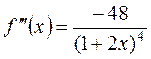 ,
, 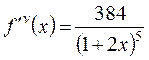
и так как функция f(x) и ее производные убывают на отрезке [0,1], то
 ,
,
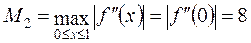 ,
,
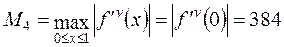 .
.
Найдем n. Для формулы прямоугольников из (9.4) получаем
 .
.
Для формулы трапеций из (9.6) получаем
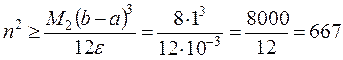 ,
, 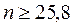 .
.
Для формулы парабол из (9.10) получаем
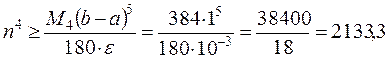 ;
; 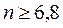 .
.
Таким образом, наименьшего объема вычислений при одинаковой точности потребует формула парабол (9.8) – n = 2m = 8 (n должно быть четным), применяя которую и вычислим приближенно заданный интеграл.
По числу n = 2m = 8 найдем шаг интегрирования 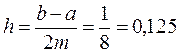 .
.
Составим таблицу (табл.1.) значений подынтегральной функции в точках xi = ih, 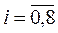 , записывая ординаты с четными и нечетными номерами в разные столбцы. В последней строке таблицы запишем результаты суммирования по этим столбцам. Вычисление будем вести с четырьмя знаками после запятой, а окончательный ответ округлим до трех знаков после запятой.
, записывая ординаты с четными и нечетными номерами в разные столбцы. В последней строке таблицы запишем результаты суммирования по этим столбцам. Вычисление будем вести с четырьмя знаками после запятой, а окончательный ответ округлим до трех знаков после запятой.
Применяя формулу парабол (9.8), получим
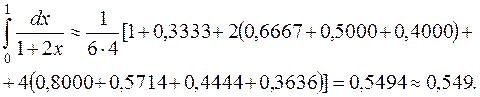
Вычислим заданный интеграл по формуле Ньютона–Лейбница
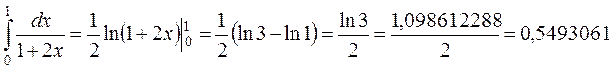 .
.
Итак, требуемая точность вычислений достигнута.
Таблица 1
| i | xi=a+ih, | 1+2хi | Значения уi=1/(1+2хi) | ||
| При i=0, i=8 | При четном i | При нечетном i | |||
| 1,0 | |||||
| 1. | 0,125 | 1,250 | 0,80 | ||
| 2. | 0,25 | 1,50 | 0,6667 | ||
| 3. | 0,375 | 1,750 | 0,5714 | ||
| 4. | 0,50 | 2,00 | 0,50 | ||
| 5. | 0,625 | 2,250 | 0,4444 | ||
| 6. | 0,750 | 2,50 | 0,40 | ||
| 7. | 0,875 | 2,750 | 0,3636 | ||
| 8. | 1,0 | 3,0 | 0,3333 | ||
| Суммы | 1,3333 | 1,5667 | 2,1794 |
Дата добавления: 2021-09-07; просмотров: 479;











